【MATLAB】入れ子関数で書く車両旋回ヨーレイトと車速の関係

概要

車両の定常円旋回時のヨーレイト $\gamma$および重心点スリップアングル $\beta$が，車両速度 $V$に対しどう変化するかを
MATLAB入れ子関数で書いた。

やったこと

ヨーレイト $\gamma$ ，重心点スリップアングル $\beta$ は以下式で算出できる。

\gamma = \frac{1}{1-\frac{m}{2l^2}\frac{l_fK_f-l_rK_r}{K_fK_r}V^2}\frac{V}{l}\delta_0\\
\beta = \frac{1-\frac{m}{2l}\frac{l_f}{l_rK_r}V^2}{1-\frac{m}{2l^2}\frac{l_fK_f-l_rK_r}{K_fK_r}V^2}\frac{l_r}{l}\delta_0

車両質量	$m$
ホイールベース	$l$
前軸-重心点距離	$l_f$
後軸-重心点距離	$l_r$
Fr コーナリングパワー	$K_f$
Rr コーナリングパワー	$K_r$
実舵角	$\delta_0$

実舵角 $\delta_0$ は3deg固定とした。

入れ子関数でヨーレイト算出式を書く

function f = calc_gamma(mf,mr,l,Kf,Kr)
f = @gamma;
    function y = gamma(V)
        m = mf+mr;
        lf = l/m*mr;
        lr = l/m*mf;
        SF = -m/(2*l^2)*(lf*Kf-lr*Kr)/(Kf*Kr);
        delta = 3/180*pi;
        v = V/3.6;
        y = 1/(1+SF*v^2)*v/l*delta;
        y = y/pi*180;
    end
end

入れ子関数で重心点スリップアングル算出式を書く

function f = calc_beta(mf,mr,l,Kf,Kr)
f = @beta;
    function y = beta(V)
        m = mf+mr;
        lf = l/m*mr;
        lr = l/m*mf;
        SF = -m/(2*l^2)*(lf*Kf-lr*Kr)/(Kf*Kr);
        delta = 3/180*pi;
        v = V/3.6;
        y = (1-m/(2*l)*lf/(lr*Kr)*v^2)/(1+SF*v^2)*lr/l*delta;
        y = y/pi*180;
    end
end

入力

carAとcarBの諸元は以下とする。
この諸元でヨーレイトの関数，重心点スリップアングルの関数を定義した。

			carA	carB
Fr mass	$m_f$	kg	900	950
Rr mass	$m_r$	kg	600	550
Total mass	$m$	kg	1500	1500
Wheelbase	$l$	mm	2500	2500
Fr tire CP	$K_f$	deg/s	1000	1000
Rr tire CP	$K_r$	deg/s	1000	1000

%% carA
mf = 900;
mr = 600;
l = 2500/1000;
Kf = 1000*180/pi;
Kr = 1000*180/pi;
g_carA = calc_gamma(mf,mr,l,Kf,Kr);
b_carA = calc_beta(mf,mr,l,Kf,Kr);

%% carB
mf = 950;
mr = 550;
l = 2500/1000;
Kf = 1000*180/pi;
Kr = 1000*180/pi;
g_carB = calc_gamma(mf,mr,l,Kf,Kr);
b_carB = calc_beta(mf,mr,l,Kf,Kr);

結果

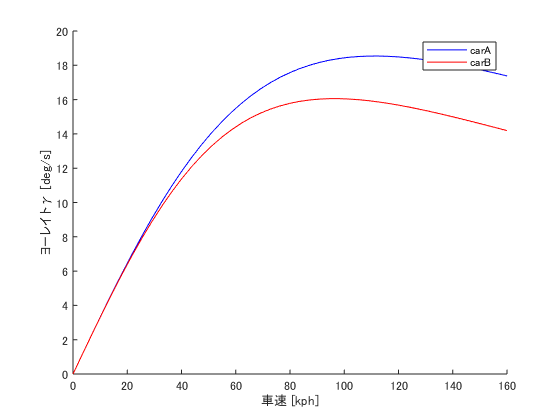
0~160kphまでをグラフ化した。

%% グラフ描画
range = [0 160];

figure(1)
hold on
fplot(g_carA,range,'b')
fplot(g_carB,range,'r')
hold off
legend('carA','carB')
xlabel('車速 [kph]')
ylabel('ヨーレイトγ [deg/s]')

figure(2)
hold on
fplot(b_carA,range,'b')
fplot(b_carB,range,'r')
hold off
legend('carA','carB')
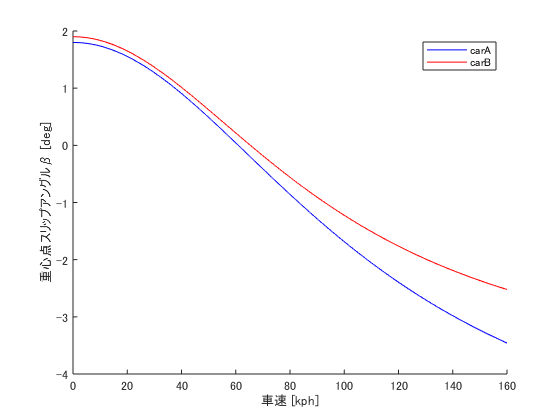
xlabel('車速 [kph]')
ylabel('重心点スリップアングルβ [deg]')

carAはcarBに比べて，低速はクイックだが，高速の穏やかさが劣ると言えそう。

carAはcarBに比べて，低速の内向き感は良い（=外向き角小さい）が，高速は内向き感が急（=内向き角の増加が急）と言えそう。

参考

安部正人，自動車の運動と制御，東京電機大学出版局，第3章

Mathworks > ヘルプセンター > 入れ子関数
https://jp.mathworks.com/help/matlab/matlab_prog/nested-functions.html