ナップサックに荷物を詰めまくる

個数制限付きナップサック問題を理解したのが嬉しかったので備忘録的にAOJのナップサック問題の一部の自分の解答をまとめます。(嘘解法が混じっている可能性があるので、その場合は指摘していただけると嬉しいです。)(最後の問題が貪欲で解けるらしいがわからなかった)

問題はこちら AOJ:組み合わせ最適化:組み合わせ

###1_A: Coin Changing Problem
DPL1_A
なるべく大きい方で払えば枚数少なくなるよね...って貪欲で考えると入出力例1に引っかかる。$i$番目までのコインを使って($i$番目を使う必要はない)、$j$円払う時に使う一番少ないコインの枚数、というのを$dp[i][j]$という風に置くと、遷移は3通りで、

1. $i$番目のコインを使わない、つまり$i-1$番目までのコインを使って$j$円払う方法をそのまま持ってくる。
2. $i-1$番目までのコインを使って$j - c[i]$円支払い、$i$番目のコインを1枚使って、$j$円払う。
3. $i$番目までのコインを使って$j - c[i]$円支払い、$i$番目のコインを1枚使って、$j$円払う。

3つの中から一番コインの枚数が少ない時が、そのまま$dp[i][j]$になる。よって漸化式は

\begin{equation}
dp[i][j] = min(dp[i-1][j], dp[i-1][j-c[i]] + 1,  dp[i][j-c[i]] + 1)
\end{equation}

イメージとしてはこんな感じ(雑)

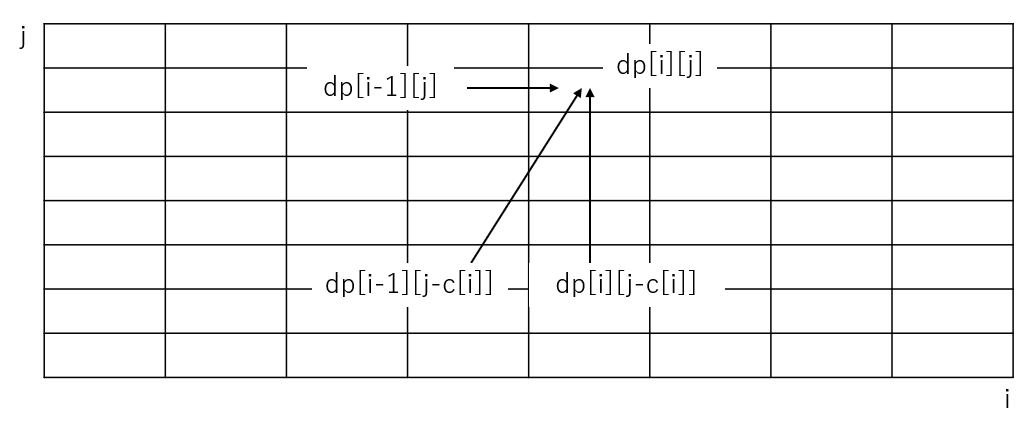
$j$が$c[i]$円より少ない場合は、$i$番目のコインを使うことは出来ないので、$dp[i-1][j]$そのまま。初期値は、どのコインも使わずに0円払う場合は、0枚のコインを使えばいいので、

dp[0][0] = 0

$m$種類それぞれのコインにすいて、$0 \sim n$円の支払い方を見ていくので計算量は$O(nm)$で、間に合う。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

#define rep(i,n) for(i = 0;i < n;++i)
#define all(v) v.begin(), v.end()
using ll = long long;

int main()
{
    ll i,j;
    ll n,m;
    cin >> n >> m;
    vector<ll> c(m);
    for(i = 0;i < m;++i){
        cin >> c.at(i);
    }
    vector<vector<ll>> dp(m+1,vector<ll>(n+1, 1e9));
    //初期値
    dp.at(0).at(0) = 0;
    for(i = 1;i <= m;++i){
        rep(j, n+1){
            //そのコインで払えない場合は、使わない場合しかない
            if(j < c.at(i-1)) dp.at(i).at(j) = dp.at(i-1).at(j);
            //そのコインで払える場合は、3通りのうちのどれか
            else dp.at(i).at(j) = min({dp.at(i-1).at(j), dp.at(i-1).at(j - c.at(i-1)) + 1, dp.at(i).at(j - c.at(i-1)) + 1});
        }
    }
    cout << dp.at(m).at(n) << endl;
    return 0;
}

###1_B:0-1 Knapsack Problem
DPL_1_B
一番典型的なナップサック問題。$i$番目までの荷物を重量$j$を超えないように一番価値が大きくなるよう荷物を入れた時の価値を$dp[i][j]$と置く。(超えないように、と置くことで、最後は$dp[N]$での値をすべて比較することなしに、$dp[N][W]$の値がそのまま答えとなっている)
遷移は2通りで、

1. $i$番目の荷物を詰めずに、$i-1$番目の荷物までを使って重量$j$を超えないように詰めた中で価値が最大となる詰め方をそのまま持ってくる。
2. $i-1$番目の荷物までを使って重量$j-w[i]$を超えないように詰めた中で価値が最大となる詰め方に、$i$番目の荷物を加える。

よって、漸化式は

dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])

$j$が小さくi番目の$w[i]$の荷物が入らない場合は、1番目の詰め方をそのまま持ってくるしかない。初期値は、何も詰めない時には重量も価値もないので、

dp[0][0] = 0

$N$種類のコインに対して、重量が$0 \sim W$までの時を見ていくので計算量は$O(NW)$

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

#define rep(i,n) for(i = 0;i < n;++i)
#define all(v) v.begin(), v.end()
using ll = long long;

int main()
{
    ll i,j;
    ll n,W;
    cin >> n >> W;
    vector<ll> v(n);
    vector<ll> w(n);
    for(i = 0;i < n;++i){
        cin >> v.at(i) >> w.at(i);
    }
    
    vector<vector<ll>> dp(n+1,vector<ll>(W+1,0));
    for(i = 1;i <= n;++i){
        rep(j, W+1){
            //その荷物を詰められない場合
            if(j < w.at(i-1)) dp.at(i).at(j) = dp.at(i-1).at(j);
            //その荷物を詰められる場合
            else dp.at(i).at(j) = max(dp.at(i-1).at(j), dp.at(i-1).at(j - w.at(i-1)) + v.at(i-1));
        }
    }
    
    cout << dp.at(n).at(W) << endl;
    return 0;
}

###1_C:Knapsack Problem
DLP_1_C
1_Bでは各荷物は1個ずつしか詰められなかったが、ここでは何個でも詰められる。考え方はコインの時と同様で、コインの時は枚数を最小にすればよかったが、ここでは価値を最大にすれば良い。よって、漸化式は、

dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i], dp[i][j-w[i]] + v[i])

計算量は同じく$O(NW)$

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

#define rep(i,n) for(i = 0;i < n;++i)
#define all(v) v.begin(), v.end()
using ll = long long;

int main()
{
    ll i,j;
    ll n,W;
    cin >> n >> W;
    vector<ll> v(n);
    vector<ll> w(n);
    for(i = 0;i < n;++i){
        cin >> v.at(i) >> w.at(i);
    }
    
    vector<vector<ll>> dp(n+1,vector<ll>(W+1,0));
    for(i = 1;i <= n;++i){
        rep(j, W+1){
            //その荷物を詰められない場合
            if(j < w.at(i-1)) dp.at(i).at(j) = dp.at(i-1).at(j);
            //その荷物を詰められる場合
            else dp.at(i).at(j) = max({dp.at(i-1).at(j), dp.at(i-1).at(j - w.at(i-1)) + v.at(i-1), dp.at(i).at(j - w.at(i-1)) + v.at(i-1)});
        }
    }
    
    cout << dp.at(n).at(W) << endl;
    return 0;
}

###1_D:Longest Increasing Subsequence
DPL_1_D
最長増加部分列問題。詳しい解説は蟻本や、最長増加部分列(LIS)の長さを求める等に詳しく載っている。
要するに$dp[i]$を、長さが$i+1$となるような増加部分列における最終要素の最小値、という風に置いておくと数列の各$j$に対して、

dp[i] = min(dp[i],a_j)

というように更新することが出来る。この時、$dp$は単調増加になるので、各$a_j$が入るところは二分探索で探すことが出来て、計算量は$O(n\log n)$で間に合う。(実際に手で具体例を書き下してみるとわかりやすい)
$dp$を始めからすべてINFで埋めておくと、答えはINFで無いところまでの長さとなる。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

#define rep(i,n) for(i = 0;i < n;++i)
#define all(v) v.begin(), v.end()
using ll = long long;

int main()
{
    ll i,j;
    ll n;
    cin >> n;
    vector<ll> a(n);
    for(i = 0;i < n;++i){
        cin >> a.at(i);
    }
    ll INF = 1e14;
    vector<ll> dp(n,INF);
    for(i = 0;i < n;++i){
        //入れられるところを二分探索
        auto itr = lower_bound(all(dp), a.at(i));
        *itr = a.at(i);
    }
    //INFとなるインデックスの一つ前までの長さが答え
    ll ans = lower_bound(all(dp), INF) - dp.begin();
    cout << ans << endl;
    return 0;
}

###1_E:Edit Distance (Levenshtein Distance)
DPL_1_E
s1の$i$番目までとs2の$j$番目までを一致させる方法を考えると、s1の$i-1$番目までとs2の$j$番目までを一致させた状態から編集するか、s1の$i$番目までとs2の$j-1$番目までを一致させた状態からs2の$i$番目を編集するか、s1の$i-1$番目までとs2の$j-1$番目までを一致させた状態から編集して一致させるか、の3通りがある。具体例1を通じてacacとacmを一致させる1段階前を考えてみると、

1. acaまでとacmまでを一致させた状態
   2. acaに一致させた場合、acm側にcを挿入する
   3. acmに一致させた場合、acac側の4文字目のcを削除する
2. acacまでとacを一致させた状態
   5. acacに一致させた場合、acm側(acacmとなっている)のmを削除する。
   6. acに一致させた場合、acac側(acとなっている)にmを挿入する。
3. acaまでとacまでを一致させた状態
   8. acaに一致させた場合、acac側はacac、acm側はacamとなっているので、どちらかに合わせる。
   9. acに一致させた場合、acac側はacc、acm側はacmとなっているので、どちらかに合わせる。

この場合、$i-1$番目と$j-1$番目までが一致している場合、$i$番目と$j$番目の文字が同じだった場合、自動的に一致するので編集する必要は無いとわかる。文章で読んでもわかりにくいので、自分の手で書き下すとわかりやすいと思う。
よって、遷移は、

dp[i][j] = max(dp[i-1][j] + 1, dp[i][j-1] + 1, dp[i-1][j-1] + cost) \\
\begin{equation}
cost = 
\begin{cases}
0 & s1[i] == s2[j]\\
1 & s1[i] != s2[j]
\end{cases}
\end{equation}

となる。
計算量は$O(|s1||s2|)$

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

#define rep(i,n) for(i = 0;i < n;++i)
#define all(v) v.begin(), v.end()
using ll = long long;

int main()
{
    ll i,j;
    string s1,s2;
    cin >> s1 >> s2;
    ll n1 = s1.size(), n2 = s2.size();
    vector<vector<ll>> dp(n1+1, vector<ll>(n2+1));
    //初期化
    for(i = 0;i <= n1;++i){
        dp.at(i).at(0) = i;
    }
    for(i = 0;i <= n2;++i){
        dp.at(0).at(i) = i;
    }
    //漸化式
    for(i = 1;i <= n1;++i){
        for(j = 1;j <= n2;++j){
            //一致する場合
            if(s1.at(i-1) == s2.at(j-1)){
                dp.at(i).at(j) = min({dp.at(i-1).at(j-1), dp.at(i-1).at(j) + 1, dp.at(i).at(j-1) + 1});
            //一致しない場合
            }else{
                dp.at(i).at(j) = min({dp.at(i-1).at(j-1), dp.at(i-1).at(j), dp.at(i).at(j-1)}) + 1;
            }
        }
    }
    cout << dp.at(n1).at(n2) << endl;
    return 0;
}

###1_F:01 Knapsack Problem Ⅱ
DPL_1_F
普通のナップサックと同様に考えようとすると、$W$のオーダーが$1e9$のため、計算量が厳しい。一方で普通のナップサックと違って価値の値が小さい。よってここは重量を基に考えるのではなく、価値を基準にしてDPを組んでいく。$i$番目までの荷物を、価値$j$となるように荷物を詰めた時に、最も軽くなるような重量を、$dp[i][j]$と置けば、計算量は$O(n^2v)$となり、間に合う。漸化式は、

dp[i][j] = min(dp[i-1][j], dp[i-1][j-v[i]] + w[i])

初期値は$dp[0][0] = 0$

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

#define rep(i,n) for(i = 0;i < n;++i)
#define all(v) v.begin(), v.end()
using ll = long long;

int main()
{
    ll i,j;
    ll n,W;
    cin >> n >> W;
    vector<ll> v(n);
    vector<ll> w(n);
    for(i = 0;i < n;++i){
        cin >> v.at(i) >> w.at(i);
    }
    ll INF = 1e14;
    ll V_MAX = 1e4;
    vector<vector<ll>> dp(n+1,vector<ll>(V_MAX+1,INF));
    dp.at(0).at(0) = 0;
    for(i = 1;i <= n;++i){
        rep(j, V_MAX+1){
            //その荷物を詰められない場合
            if(j < v.at(i-1)) dp.at(i).at(j) = dp.at(i-1).at(j);
            //その荷物を詰められる場合
            else dp.at(i).at(j) = min(dp.at(i-1).at(j), dp.at(i-1).at(j - v.at(i-1)) + w.at(i-1));
        }
    }
    //重さの条件を満たす一番大きい価値が答え
    for(i = V_MAX;i >= 0;--i){
        if(dp.at(n).at(i) <= W){
            cout << i << endl;
            return 0;
        }
    }
    return 0;
}

###1_G: Knapsack Problem with Limitations
DPL_1_G
というわけでようやく出てきたこれが本題。以下の解説は蟻本を参考にしているので、もしかしたら蟻本の方が簡潔でわかりやすいかもしれない...。個数制限が付いたので、個数無制限の時のように下から適当に漸化式を回すことは出来ない。一方で、$i-1$個まで詰めた状態から、$m[i]$個下から順に何個詰められるか、と見ていくと計算量が$O(NWm)$となってしまい、これでは間に合わない。というわけで以下の様に考えていく。
$dp[i][j]$に遷移してくる元の場所について考えてみると、$dp[i-1][j-w[i]], dp[i-1][j-2w[i]]...dp[i-1][j-kw[i]]...dp[i-1][max(j-m[i]w[i], j%w[i])]$のいずれか。雑なイメージが下。

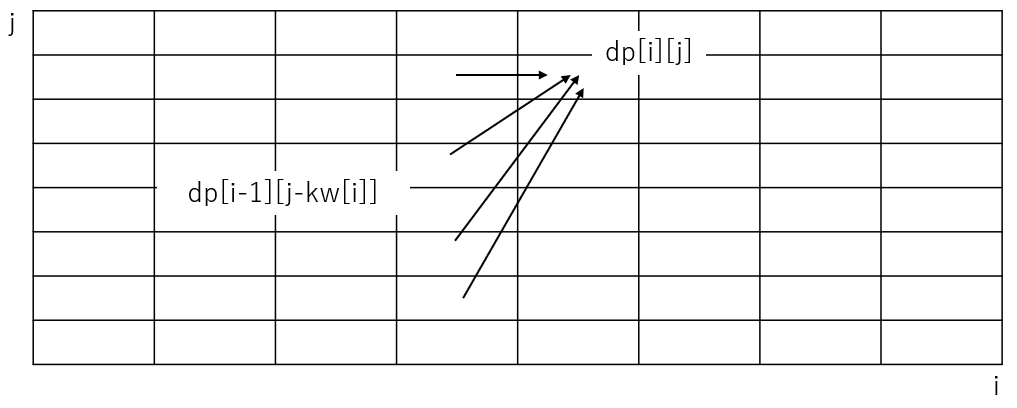
要するに、dp[i][j]は、dp[i-1][l]で、$a \equiv j \bmod w[i]$となるような$l$のみ考えれば良い。この時、

dp[i][j] = max(dp[i-1][j - kw[i]] + kv[i])

が漸化式となる。
ここで、$dp[i][j]$にとって$dp[i-1][j-w[i]]$は、$dp[i-1][j-w[i]] + v[i]$の価値を持つが、$dp[i][j-w[i]]$にとっては$dp[i-1][j-w[i]] + v[i]$の価値しか持たない。要するに自分から離れているほど、その分価値が上がる可能性がある。が、今はmodで統一して考えたいので、これは不便である。ここで、

a = j\%w[i], j = a + kw[i] \\
b[k] = dp[i-1][a + kw[i]] - kv[i]

というように新しく変数を置くと、$dp[i][a+kw[i]]$にとって、

dp[i-1][a+kw[i]] からは dp[i-1][a+kw[i]] = b[k] + kv[i] \\
dp[i-1][a+(k-1)w[i]] からは dp[i-1][a+(k-1)w[i]] + v[i] = b[k-1] + kv[i]

と、すべて$b[k]$の大小がそのまま、そのdpに関する価値の大小になってくれる。また、$dp[i][a+(k-1)w[i]]$にとっての価値を考えてみると、

dp[i-1][a+(k-1)w[i]] からは dp[i-1][a+(k-1)w[i]] =b[k-1] + (k-1)v[i] \\
dp[i-1][a+(k-2)w[i]] からは dp[i-1][a+(k-2)w[i]] + v[i] = b[k-2] + (k-1)v[i]

と、足すものこそ変わるものの、$b[k]$を元にして考えれば良いことに変わりはない。よって、$dp[i][j] = dp[i][a + kv[i]]$が最大となるように$b[l]$$(max(k - m[i], 0) \leq l \leq k)$の最大値を持ってくればよい。あとは、$b[l]$をスライド最小値的に考えていけばよい。スライド最小値は、Silver Fox vs Monsterでqueueを使う考え方でその爆弾の効果範囲を考えたように、ここでもその$b[l]$が取られる場合の期限をdequeで管理してやればよい。例としては、

b = {5,3,2,6,6} \\
m = 2 \\
deque = \{\} \\

というようになっていたとすると、

1. k = 0の時、dequeは空なので、deque = {(5,2)}と追加する。(2つ目の2は、m = 2なので、k = 2の時まで有効の意味) 。dequeの先頭を持ってきて、$dp[i][a]$にとってのbの最大値は、5。
2. k = 1の時、dequeに{(3,3)}を追加する。deque = {(5,2),(3,3)}。最大値はdequeの先頭を持ってきて5。
3. k = 2の時、dequeに{(2,4)}を追加する。deque = {(5,2),(3,3),(2,4)}。最大値はdequeの先頭を持ってきて5。ここで、先頭の有効期限は2までで、k = 3以降では使えないので、(5,2)をpopして、deque = {(3,3),(2,4)}。
4. k = 3の時、b[3] = 6は今から有効なので、それより小さい(3,3),(2,4)が最大となることはあり得ないので、両方ともpopされて、6を追加し、deque = {(6,5)}。最大値はdequeの先頭を持ってきて6。
5. k = 4の時、同じ値では、有効期限が長い方が良いので、6はpopされて6を追加し、deque = {(6,6)}。最大値はdequeの先頭を持ってきて6。
   各modごとに考えるが、結局各$w$を一回ずつ訪れるだけなので、各$i$での計算量は$W$。よって全体の計算量は$O(NW)$で済む。以上を実装して、下。

#include <iostream>
#include <vector>
#include <deque>
using namespace std;

#define rep(i,n) for(i = 0;i < n;++i)
#define all(v) v.begin(), v.end()
using ll = long long;

int main()
{
    ll i,j;
    ll n, W;
    cin >> n >> W;
    vector<ll> v(n);
    vector<ll> w(n);
    vector<ll> m(n);
    for(i = 0;i < n;++i){
        cin >> v.at(i) >> w.at(i) >> m.at(i);
    }
    vector<vector<ll>> dp(n+1, vector<ll>(W+1,0));
    for(i = 1;i <= n;++i){
        ll a;
        //modでそれぞれ考える。
        rep(a, w.at(i-1)){
            //スライド最小値のためのdeq
            deque<pair<ll,ll>> deq;
            for(j = 0;j*w.at(i-1) + a <= W;++j){
                //それぞれでの重さ
                ll tmpw = j*w.at(i-1) + a;
                //b[j]の値
                ll val = dp.at(i-1).at(tmpw) - j*v.at(i-1);
                //空ではない時、valより小さい値はもう使わない。
                while((!deq.empty()) && deq.back().first <= val) deq.pop_back();
                deq.emplace_back(val, j);
                //先頭が最大で、漸化式の計算に使われる。
                dp.at(i).at(tmpw) = deq.front().first + j*v.at(i-1);
                //期限が来たらpop
                if(j - deq.front().second == m.at(i-1)) deq.pop_front();
            }
        }
    }
    cout << dp.at(n).at(W) << endl;
    return 0;
}

###1_H: Huge Knapsack Problem
DPL_1_H
$v[i] \leq 10^{15}, w[i] \leq 10^{15}, W \leq 10^{15}$と$v$も$w$も$W$も大きすぎて、$O(n^2v)$も$O(nW)$も使えない。と$n$を見ると$n \leq 40$と$n$だけ極端に小さい。が$n$についてbit全探索しても$2^{40} \simeq 10^{12}$なので間に合わない。が、$n$を半分にして分ければ、$2^{20} \simeq 10^6$より$O(n\log n)$までなら間に合うようになる。ここで、前半について、あり得る$(w,v)$の組み合わせを列挙して考えると、$w$が同じ時は$v$が最大の時しか使われない。また、$w$がより重いのに、$v$が少ない場合も使われない。よって、列挙された$(w,v)$から選んで並び替えることで、$w_i > w_j$ならば$v_i > v_j$となるようにペアの列を作ることが出来る。よって片方の列を固定して、$(w_i,v_i)$に対して、重量が$W - w_i$以下で一番重い重量のものを二分探索で選ぶの最適となる。片方の列を固定した状態で、もう片方の列から二分探索するので、計算量は$O(2^{n/2}\log 2^{n/2})$

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

#define rep(i,n) for(i = 0;i < n;++i)
#define all(v) v.begin(), v.end()
using ll = long long;

int main()
{
    ll i,j;
    ll n,W;
    cin >> n >> W;
    vector<ll> v(n);
    vector<ll> w(n);
    for(i = 0;i < n;++i){
        cin >> v.at(i) >> w.at(i);
    }
    //前半のペアについてbit全探索
    ll n2 = n/2;
    vector<pair<ll,ll>> tmp_sum1;
    for(ll bit = 0;bit < (1 << n2);++bit){
        ll w_sum = 0;
        ll v_sum = 0;
        for(i = 0;i < n2;++i){
            if(bit & (1 << i)){
                w_sum += w.at(i);
                v_sum += v.at(i);
            }
        }
        //vを-にソートすることで、全体でwが軽い順に、同じwの中ではなるべくvが大きくなるようにソートされる
        if(w_sum <= W) tmp_sum1.emplace_back(w_sum,-v_sum);
    }
    sort(all(tmp_sum1));
    //単調増加となるようにペアを選別していく。
    vector<pair<ll,ll>> sum1;
    for(i = 0;i < tmp_sum1.size();++i){
        ll w_sum = tmp_sum1.at(i).first;
        ll v_sum = -tmp_sum1.at(i).second;
        if(i == 0){
            sum1.emplace_back(w_sum, v_sum);
        }else{
            if(sum1.back().second < v_sum) sum1.emplace_back(w_sum, v_sum);
        }
    }
    //後半も同様に作る
    ll n22 = n - n2;
    vector<pair<ll,ll>> tmp_sum2;
    for(ll bit = 0;bit < (1 << n22);++bit){
        ll w_sum = 0;
        ll v_sum = 0;
        for(i = 0;i < n22;++i){
            if(bit & (1 << i)){
                w_sum += w.at(i + n2);
                v_sum += v.at(i + n2);
            }
        }
        if(w_sum <= W) tmp_sum2.emplace_back(w_sum,-v_sum);
    }
    sort(all(tmp_sum2));
    vector<pair<ll,ll>> sum2;
    for(i = 0;i < tmp_sum2.size();++i){
        ll w_sum = tmp_sum2.at(i).first;
        ll v_sum = -tmp_sum2.at(i).second;
        if(i == 0){
            sum2.emplace_back(w_sum, v_sum);
        }else{
            if(sum2.back().second < v_sum) sum2.emplace_back(w_sum, v_sum);
        }
    }
    //2つを組み合わせて二分探索
    ll ans = 0;
    for(i = 0;i < sum1.size();++i){
        ll w_sum = sum1.at(i).first;
        ll v_sum = sum1.at(i).second;
        auto itr = lower_bound(all(sum2), make_pair(W-w_sum+1, 0ll));
        if(itr != sum2.begin()) ans = max(ans, v_sum + (*--itr).second);
    }
    cout << ans << endl;
    return 0;
}

###1_I: Knapsack Problem with Limitations Ⅱ
DPL_1_I
解けてません。ごめんなさい
nとvが小さいが、個数制限の条件が付いたのでHの方法は使えない。また、mの条件が大きいので、Gでやった方法をスライド最小値に置き換える方法も使えない。個数制限付きナップサック Luzhiled's memo(Knapsack-Limitations)によると、一部は貪欲に取れるらしいですが、わかりませんでした...。