前書き
こちらのサイト(その8 4分木空間分割を最適化する!(理屈編))を
読んで、曖昧ながらも理解できたのでその備忘録
リンク先のサイトで完結しているので頭のいい人は以下の文章は見なくていいです。
四分木空間分割
図1

オブジェクトA~Gのすべての衝突判定を行うとして
考えなしに行う場合、
AとB~G、BとC~G、CとD~G、…
と衝突判定をすると思うが、左上にあるAと右下にあるGは明らかに衝突し得ないため、そもそも判定を行わないようにしたい。
そこで空間を再帰的に四分割し衝突している可能性があるオブジェクトのみで衝突判定を行うようにする。
図1では空間を四分割し、さらに分割された空間を四分割している。
以後、四分割は再帰的に2回行うものとする。
空間の分割
次のように分割された空間に識別番号を付ける。
色付きの数字は二進数、黒色の数字は十進数を表わしている。
四分割1回

四分割2回

四分割された空間は左上、右上、左下、右下の順に二進数で00、01、10、11と識別番号が割り当てられる。
親空間が存在する場合は、親空間の識別番号が先頭につく。
(つまり、自身の識別番号から親の識別番号を知ることができる。)
属している空間を求める
図1の各オブジェクトがどの空間に属するか考える。
図1

Aは四分割2回の0~3番に属しているように見えるが、それらはAを内包していないため違う。
四分割1回の0番はAを内包しているため、Aは四分割1回の0番に属すことになる。
各オブジェクトは次の空間に属している。
| オブジェクト | 四分割回数 | 番号 |
|---|---|---|
| A | 1回 | 0番 |
| B | 2回 | 4番 |
| C | 2回 | 7番 |
| D | 0回 | 0番 |
| E | 1回 | 2番 |
| F | 2回 | 14番 |
| G | 1回 | 3番 |
ツリーで表わすとこうなる。
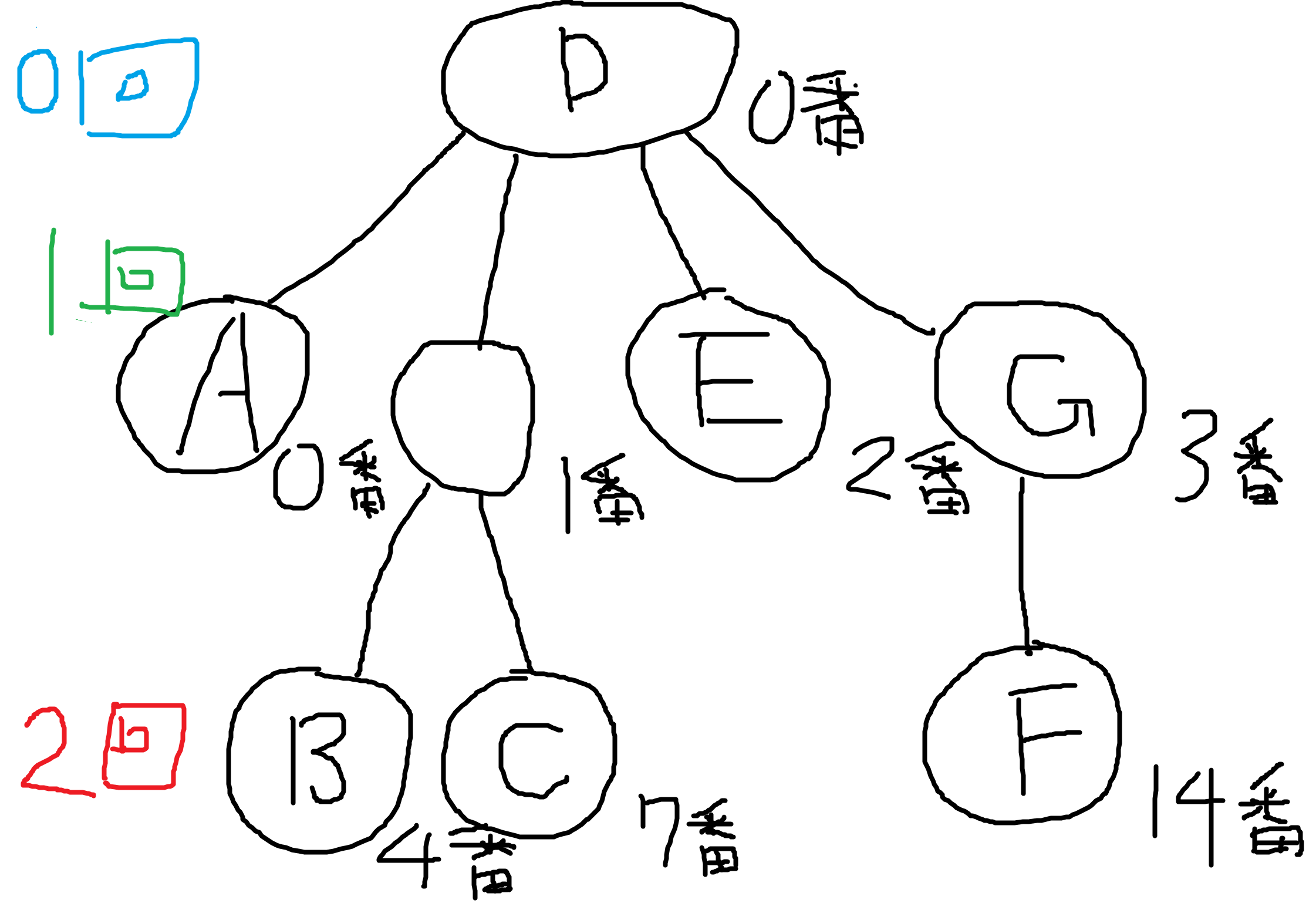
仮にオブジェクトHが1回0番に属している場合はA、Dと、
1回1番に属している場合はB、C、Dと、
0回0番に属している場合は全オブジェクトと衝突判定をすればよい。
つまり特定のオブジェクトの衝突判定は、
・そのノードに属する全オブジェクト
・そのノードの再帰的な親ノードに属する全オブジェクト
・そのノードの再帰的な子ノードに属する全オブジェクト
にする必要がある。
それはさておき、上にのせた各オブジェクトの属する空間は私が目で判定したものであり、
実際はプログラムで判定しなければならない。
次の手順でオブジェクトの属する空間を求めることが出来る。
- オブジェクトの左上と右下の点の座標が属する四分割2回の空間の番号を求める。
- 左上と右下の四分割2回の空間番号でビットごとの排他的論理和をとり、オブジェクトが四分割の何回目(Nとする)の空間に属しているかを求める。
- 左上(右下でもよい)の四分割2回の空間番号と2.で求めたNから、オブジェクトが四分割N回の何番に属しているのかを求める。
実際にオブジェクトGが属する空間を求めてみる。
なおオブジェクトGの左上の座標は(80, 60)、右下の座標は(90, 90)とする。
1. 左上と右下の座標の空間番号を求める。
座標のx, yを四分割2回の空間の幅($= 100 \ \div \ 2 ^ 2 \ = \ 25$)で割り、小数点以下を切り捨てると四分割2回0番からx軸方向の何番目、y軸方向の何番目の空間が対象か分かる。
オブジェクトGの左上と右下の座標
左上: $(80, 60) \rightarrow (3.2, 2.4) \rightarrow (3, 2)$ 四分割2回0番からx軸方向の3番目、y軸方向の2番目の空間に属している。
右下: $(90, 90) \rightarrow (3.6, 3.6) \rightarrow (3, 3)$ 四分割2回0番からx軸方向の3番目、y軸方向の3番目の空間に属している。
細かいこと
さて、xy軸方向何番目の位置にある空間か分かったので対応表を作り、それを利用して空間番号を求めてもいいが、ビットをいじくりまわしても求めることができる。
オブジェクトGの左上と右下の座標を用いて説明する。
上手い説明できないので読者はエスパーになってもらいたい。
理解できない場合は冒頭のサイトの「点の座標値から所属するモートン空間番号を出す」を参考
左上の座標は四分割2回からx軸方向の3番目、y軸方向の2番目の空間に属している。
x軸方向の3番目 → 3 → 二進数で011 → (x1, x2, x3) = (0, 1, 1)と定義
y軸方向の2番目 → 2 → 二進数で010 → (y1, y2, y3) = (0, 1, 0)と定義
二進数 y1 x1 y2 x2 y3 x3 → 0 0 1 1 0 1 → 001101 → 十進数で13 → 四分割2回の13番の空間に属していると分かる。
同様に
右下の座標は四分割2回からx軸方向の3番目、y軸方向の3番目の空間に属している。
x軸方向の3番目 → 3 → 二進数で011 → (x1, x2, x3) = (0, 1, 1)と定義
y軸方向の3番目 → 3 → 二進数で011 → (y1, y2, y3) = (0, 1, 1)と定義
二進数 y1 x1 y2 x2 y3 x3 → 0 0 1 1 1 1 → 001111 → 十進数で15 → 四分割2回の15番の空間に属していると分かる。
2. オブジェクトの属している空間が四分割何回目か求める。
左上と右下の四分割2回の空間番号でビットごとの排他的論理和をとると、オブジェクトが四分割の何回目の空間に属しているかが分かる。
オブジェクトGの左上の座標は四分割2回の13番、右下の座標は四分割2回の15番なので
$13 \ \oplus \ 15 \ = \ (001101)_2 \ \oplus \ (001111)_2 \ = \ (000010)_2$となる。

四分割0回のXORが0 → オブジェクトGは四分割0回のどこかの空間に属している。
四分割1回のXORが0 → オブジェクトGは四分割1回のどこかの空間に属している。
四分割2回のXORが0でない → オブジェクトGは四分割2回のどこかの空間に属していない。
よってオブジェクトGが四分割1回のいずれかの空間に属していることが分かった。
証明は属するときのパターンで0になること、属さないときに0にならないことを四分割の図を眺めれば何となく分かるので略
3. オブジェクトの属している空間番号を求める。
2.よりオブジェクトGが四分割1回のどこかの空間に属していることが分かった。
そして空間番号の識別ルールより、オブジェクトGの内の点が属する四分割2回の空間の番号から自身を含んでいる四分割N回(N < 2)の空間の番号を知ることができる。
オブジェクトGの左上の座標が属している四分割2回の空間の番号は001101なので四分割1回の空間番号が$(11)_2 \ = \ 3$となり、オブジェクトGは四分割2回の3番の空間に属していることが分かった。
全オブジェクトとの衝突判定
属している空間を求めるにも書いたが
あるオブジェクトの衝突判定は、
・そのノードに属する全オブジェクト
・そのノードの再帰的な親ノードに属する全オブジェクト
・そのノードの再帰的な子ノードに属する全オブジェクト
にする必要がある。

よってオブジェクトA~Gのすべての衝突判定をする場合
$(D, A), \ (D, B), \ (D, C), \ (D, E), \ (D, G), \ (D, F), \ (G, F)$
と行えばよい。
なお冒頭のサイトの「④ 1回の木巡回で衝突判定を終わらせる」は

と探索するより

とした方がロジック的によくない?ということを言っている。(多分)
終わり。


