前書き
これを読む人はパスカルの三角形もシェルピンスキーのギャスケットも余裕で知っていると思うので説明しない。
知らない人は以下を参考
言葉の定義
以下のリンク先の図形を「法2のギャスケット」もしくは「2を法とするギャスケット」と呼ぶことにする。
https://mogamoga1024.github.io/PascalsTriangle/?mod=2&rowCount=512
なお法nのギャスケットはnで割りきれない箇所を黒で塗りつぶしている。
気づいたこと
次のギャスケットに法則性が存在する可能性を発見した。(既知かは知らない)(自分は未証明)
- 素数pを法とするギャスケット
- 素数pのn乗を法とするギャスケット
- 合成数を法とするギャスケット
1. 素数pを法とするギャスケット
法2のギャスケット

https://mogamoga1024.github.io/PascalsTriangle/?mod=2&rowCount=512
法3のギャスケット
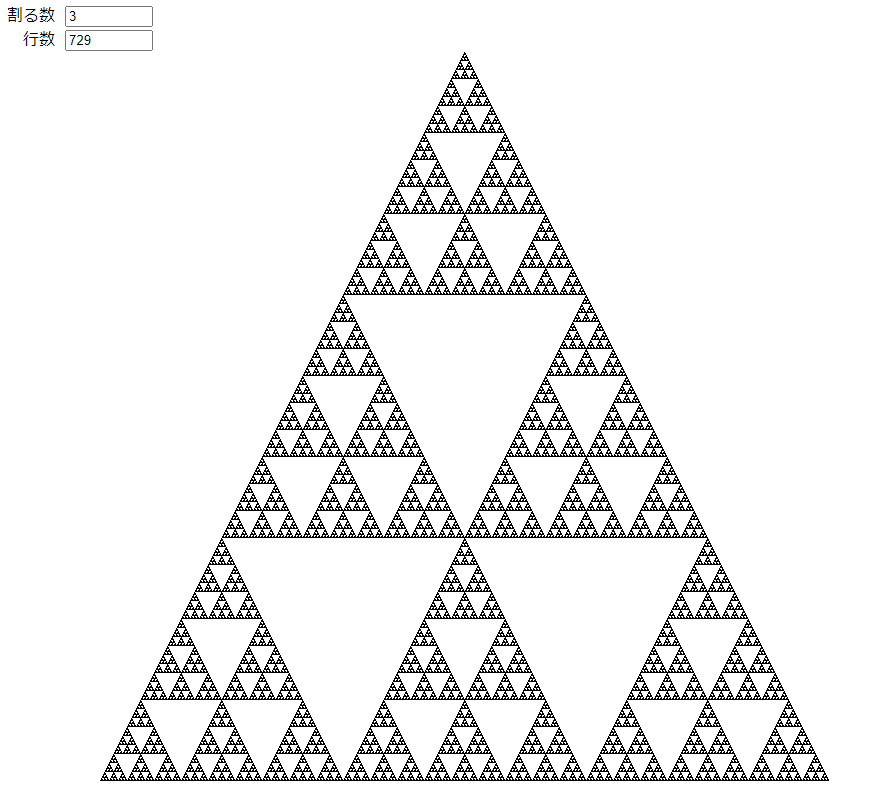
https://mogamoga1024.github.io/PascalsTriangle/?mod=3&rowCount=729
法5のギャスケット

https://mogamoga1024.github.io/PascalsTriangle/?mod=5&rowCount=625
定義
次のように定義する。


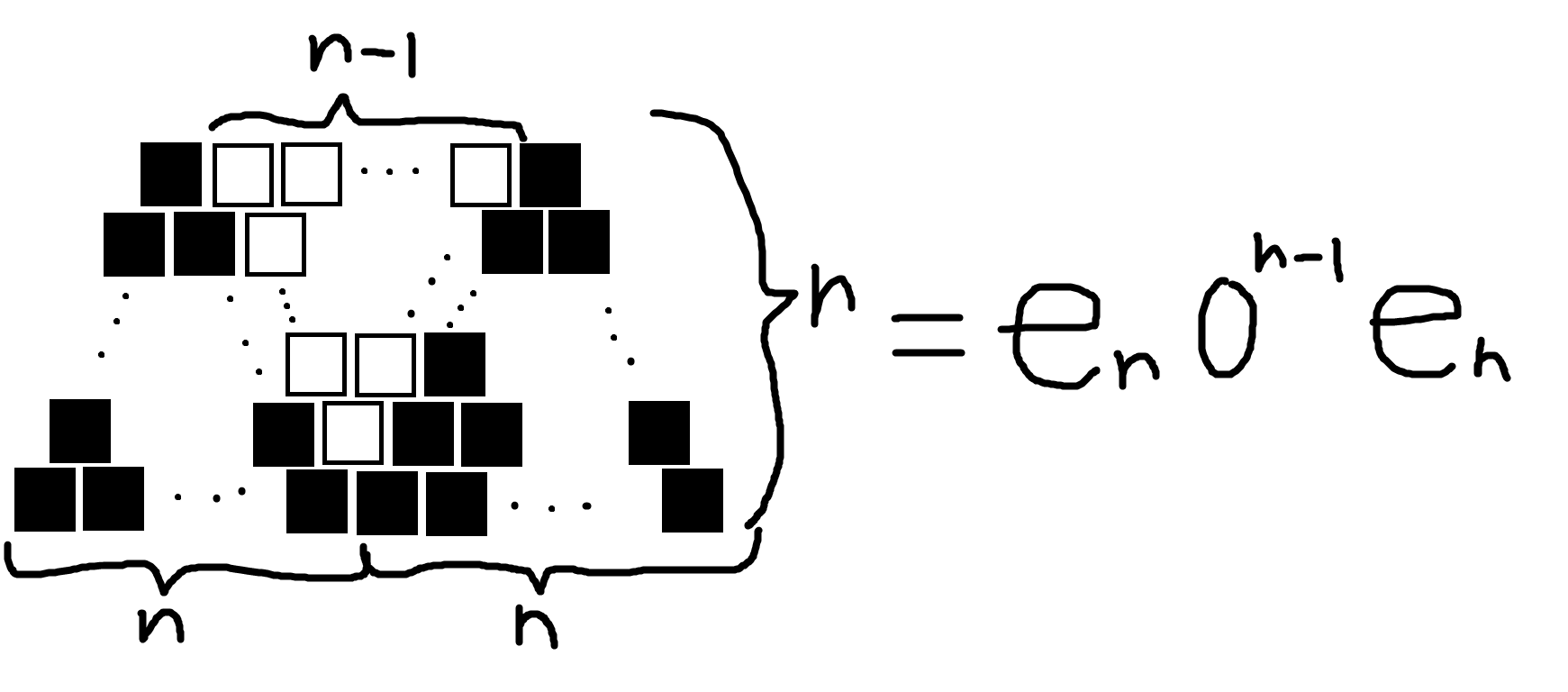
予想
次の式が成立すると考えられる。
関数fはx回の再帰的な構造を持つ法pのギャスケットを表す。

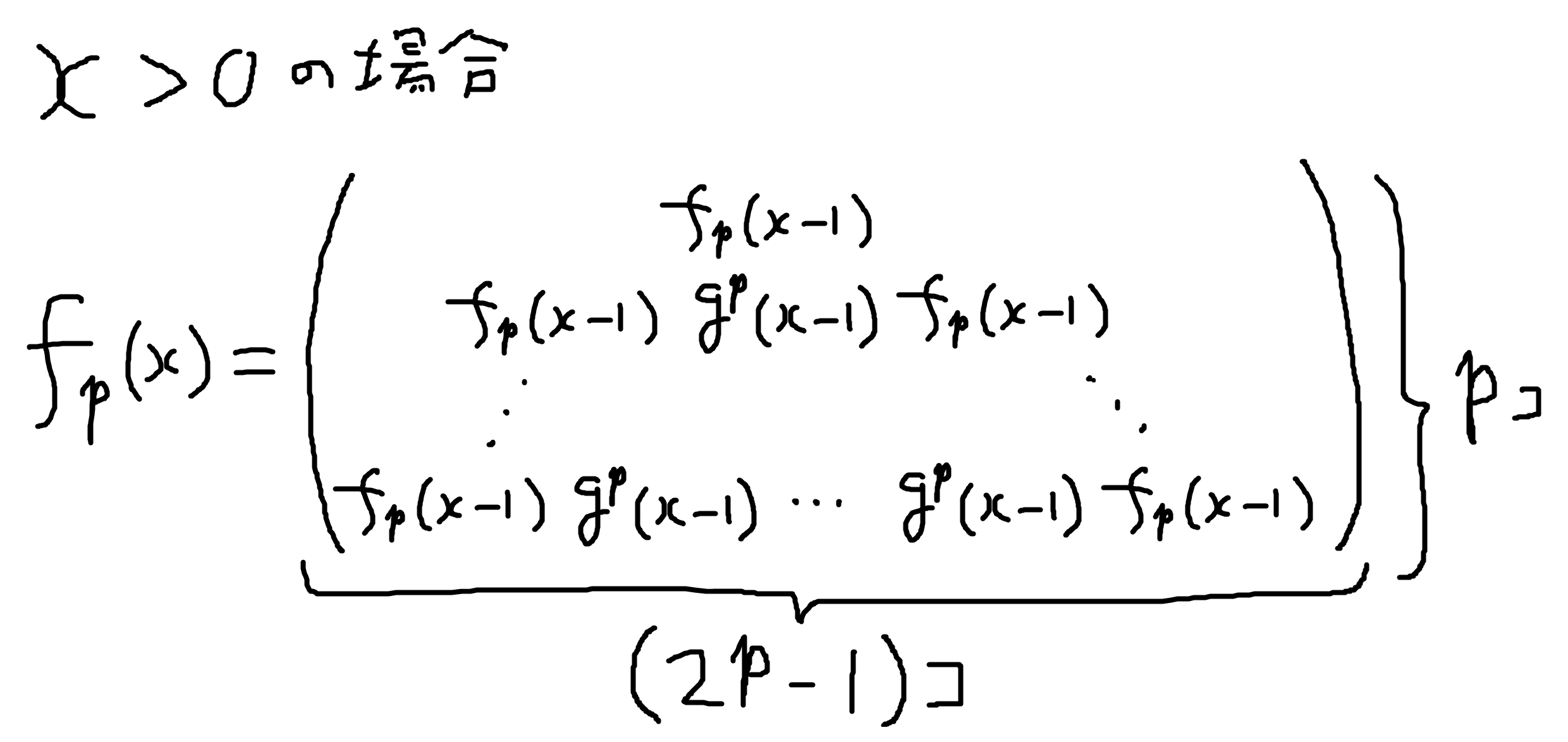
2. 素数pのn乗を法とするギャスケット
法2^2のギャスケット

https://mogamoga1024.github.io/PascalsTriangle/?mod=4&rowCount=512
法2^3のギャスケット

https://mogamoga1024.github.io/PascalsTriangle/?mod=8&rowCount=512
法3^2のギャスケット

https://mogamoga1024.github.io/PascalsTriangle/?mod=9&rowCount=729
法3^3のギャスケット

https://mogamoga1024.github.io/PascalsTriangle/?mod=27&rowCount=729
予想
次の式が成立すると考えられる。
関数fはx回の再帰的な構造を持つ法p^nのギャスケットを表す。

3. 合成数を法とするギャスケット
法6のギャスケット

https://mogamoga1024.github.io/PascalsTriangle/?mod=6&rowCount=729
予想
ある法aのギャスケットがあるとする。
aが次のように素因数分解された場合
$a = p \times q^n \times r ^ m$
法aのギャスケットは
法pのギャスケット、法q^nのギャスケット、法r^mのギャスケットを重ねたものと一致する。