配列をランダムにシャッフルするFisher–Yates shuffleを通して標準偏差について知った話

この記事は個人的な気付きの覚書です。
当たり前のことでしかないので、特に新しい発見などはありません。
Fisher-Yates shuffleを知らない、標準偏差を知らない、暇だ、という方向けです。

Fisher-Yates shuffleとは

配列の要素を偏りなくランダムにシャッフルするアルゴリズムです。

経緯

Fisher-Yates shuffleのアルゴリズムとして知られるコードは

for (let i = arr.length - 1; i > 0; i -= 1) {
  const j = Math.floor(Math.random() * (i + 1));
  [arr[i], arr[j]] = [arr[j], arr[i]];
}

ですが、検索していると

for (let i = arr.length - 1; i >= 0; i -= 1) {
  const j = Math.floor(Math.random() * (i + 1));
  [arr[i], arr[j]] = [arr[j], arr[i]];
}

というコードも見かけます。
微妙な違いですが、for文の中のi > 0とi >= 0の違いです。
後者のコードの実装で、結果に偏りがあるのでは？という指摘を見て
この違いで結果がどう変わってくるのか興味が湧きました。
そしてその過程で「標準偏差」について知りました。

結論：結果に差はない（はず）

結論から言うと恐らく結果に差はありません。
ただi >= 0は余計な処理を発生させるので関数を実行する回数が多い場面では避けるべきです。
以下は結果に差が出ないという結論に至るまでの検証の記録です。

結果を可視化

漠然とコードを見ていてもさっぱりなので実際に動かしてみました。

See the Pen Fisher–Yates shuffle Example by m_og (@m_og) on CodePen.

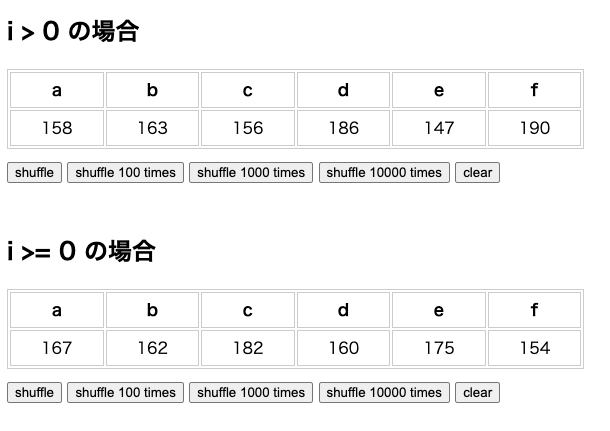
表の数字は、arr = ["a", "b", "c", "d", "e", "f"]の配列をシャッフルしたときに、それぞれのアルファベットが配列の1番目にきた回数を数えています。
ボタンは「shuffle」で一回シャッフル、「shuffle ○○ times」で○○回シャッフルします（数字が大きいほどラグが発生します）。

アルゴリズムの仕組み

このアルゴリズムの動きとしては
arr[5]、arr[4]、arr[3]…と順番に配列の中身を参照して、参照された要素と、その要素かそれより若いインデックスの要素を置き換えることをarr[i]まで繰り返す、というものです。

i >= 0は無駄な動きをする

1文字ずつシャッフルされるたびに結果をコンソールで確認するとよくわかりますが、
i >= 0の場合最後に「arr[0]とarr[0]を置き換える」という必要がない処理が走ることがわかります。
処理速度に影響することは分かりましたが「均等なシャッフル」とどう関係しているのか…。
均等かどうかを知ることができる標準偏差という指標を見てみます。

分散と標準偏差

分散・標準偏差とは、全体のばらつき具合を数値で表したものです。
詳しくはこちらのサイトが参考になりました。
統計学における分散とは？不偏分散との違いも！ 例題でわかりやすく解説 | AVILEN AI Trend
まず全体の平均値を求めます。
各数値から平均値を引いた値を2乗した数値の平均が分散といい（2乗するのは正数にするためです）、
分散の平方根をとったものが標準偏差です。
値が大きいほど、数値にばらつきがあるということになります。

100回、1000回、10000回繰り返してみたときの標準偏差

使用したサイトはこちら。

100回の例

	i > 0	i >= 0
数字の合計：	100.0	100.0
平均（平均）値：	16.6666666667	16.6666666667
母集団標準偏差（σ）：	4.85340659285	4.53382350291
母分散（P 2）：	23.5555555556	20.5555555556

1000回の例

	i > 0	i >= 0
数字の合計：	1000.0	1000.0
平均（平均）値：	166.666666667	166.666666667
母集団標準偏差（σ）：	15.8499912373	9.41039614233
母分散（P 2）：	251.222222222	88.5555555556

10000回の例

	i > 0	i >= 0
数字の合計：	10000.0	10000.0
平均（平均）値：	1666.66666667	1666.66666667
母集団標準偏差（σ）：	36.6545434504	36.8721514907
母分散（P 2）：	1343.55555556	1359.55555556

私は何をしているんだろう

言うまでもなく、i >= 0の場合に最後に走る「arr[0]とarr[0]を置き換える」という処理の違い以外に、ふたつのアルゴリズムに差はありません。
配列の並びに影響する操作ではないため、標準偏差の違いは完全にMath.random()の値に依存しています。
しかし実験を繰り返す中で、i >= 0の標準偏差の方が値が大きくなるという場面が多々あり、
全ての始まりである「結果に偏りがあるのでは？」という指摘のあった部分も、修正の結果偏りが解消されたように感じられました。不思議ですね…気のせいなはずなのに…。

アルゴリズムの検証は大事

今回、初めてアルゴリズムの仕組みを検証する、ということを行いました。
検索して出てきたアルゴリズムは深く考えずに、結果が求めていたものに近ければそのまま採用してしまうことがほとんどでした。
ソース元の信頼性も大切ですが、余裕があれば自分自身によるダブルチェックの機会を設けることも大切ですね。
無駄のない正しいアルゴリズムを使えるように心がけたいです。