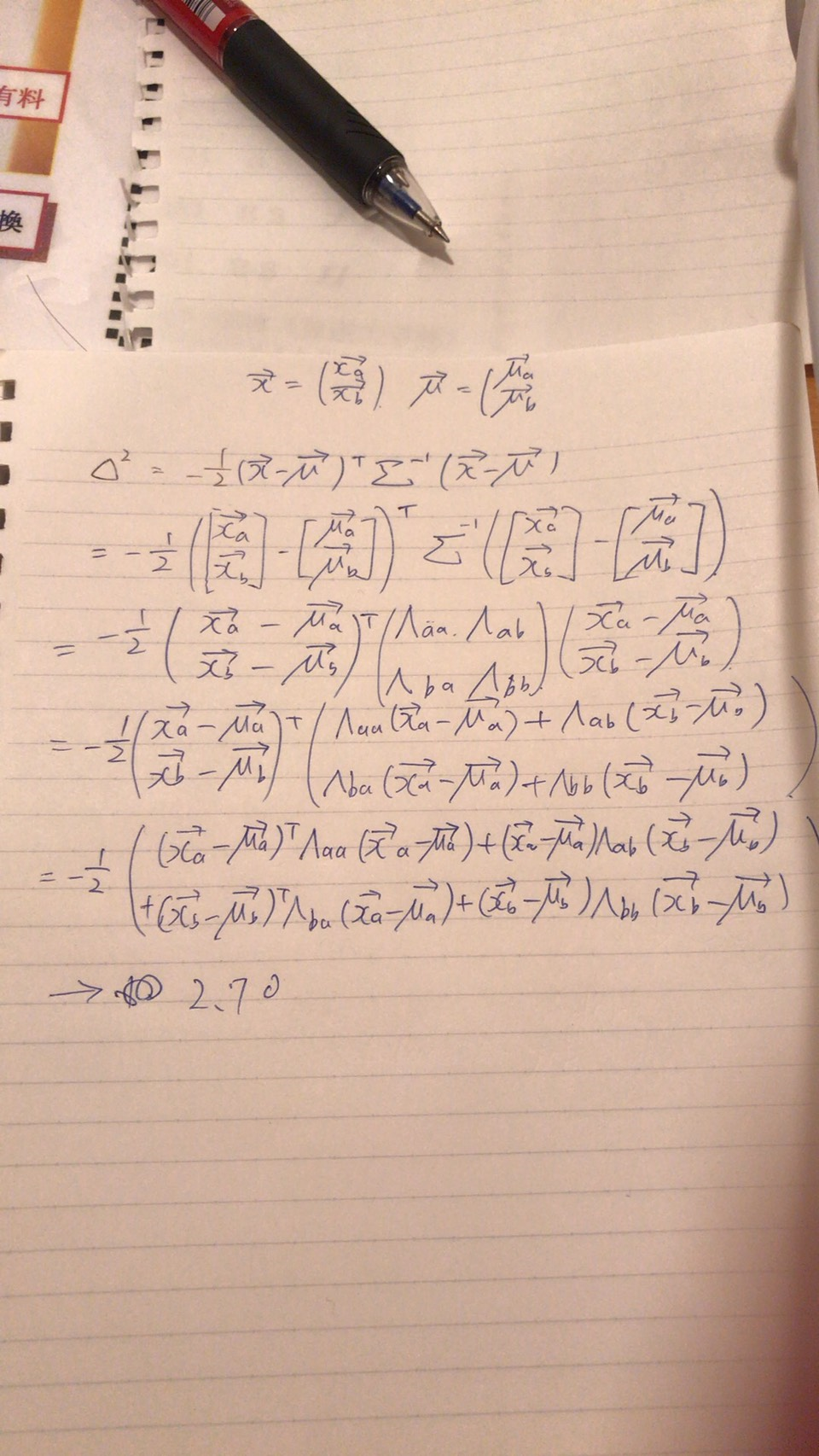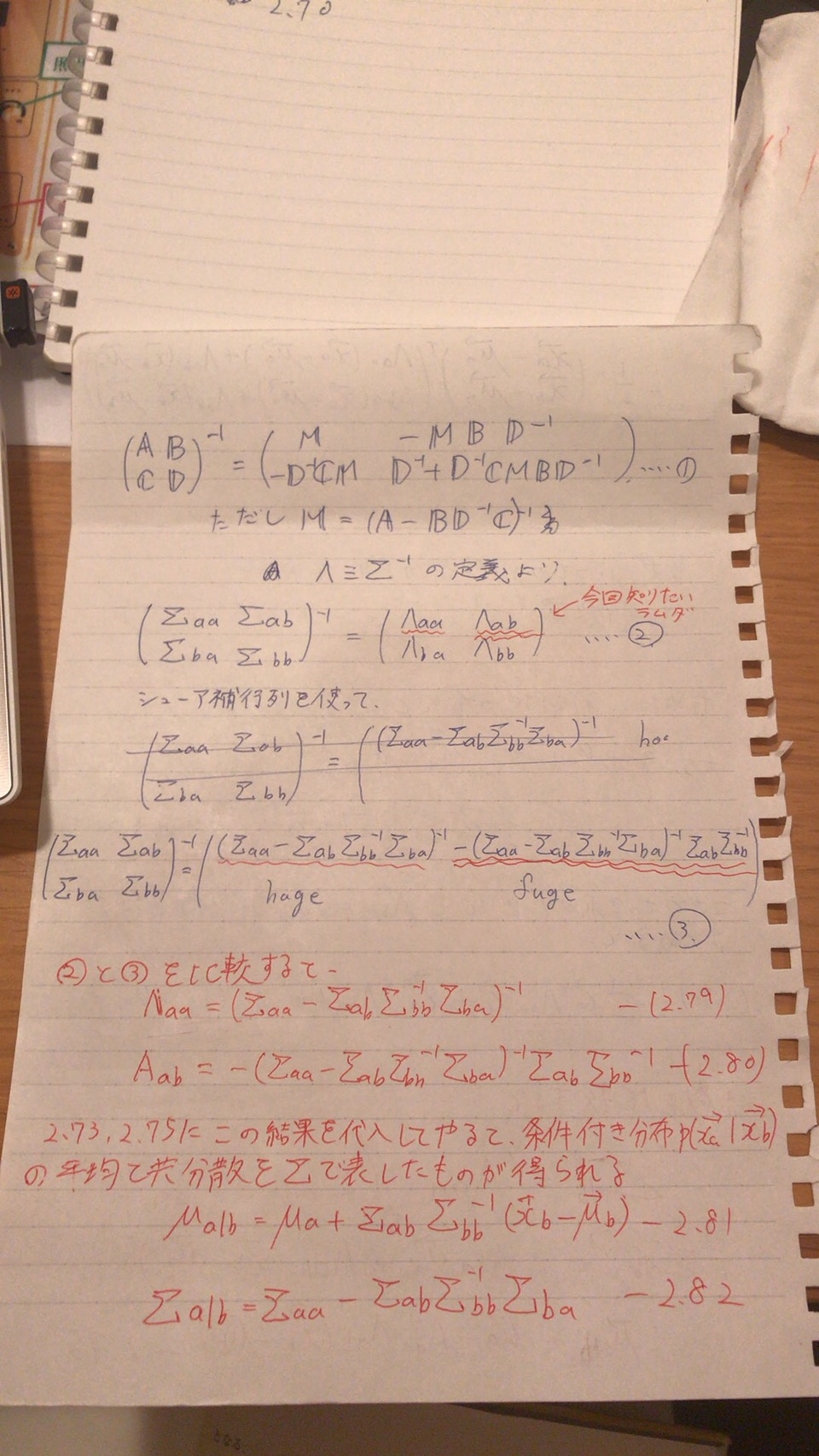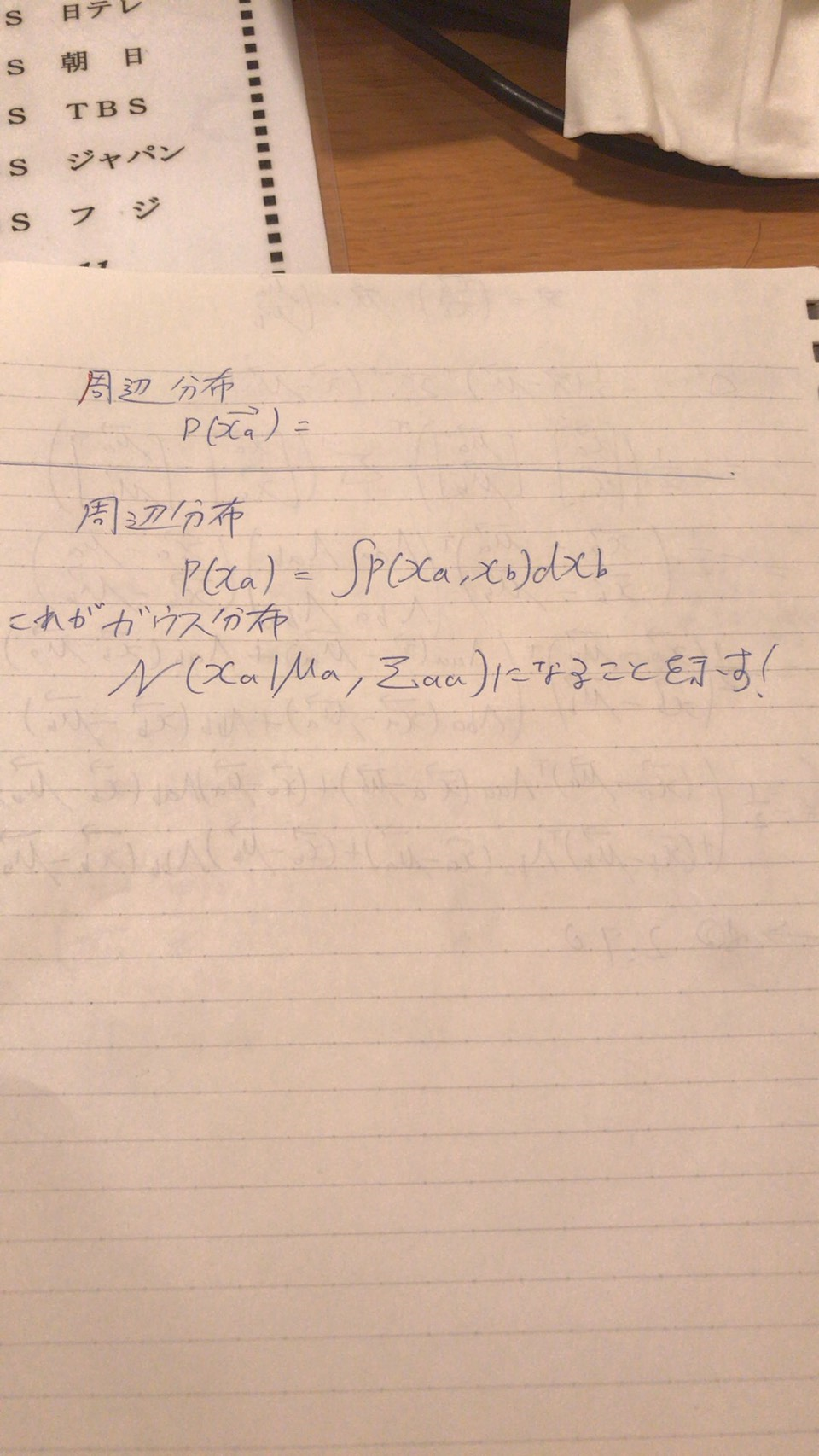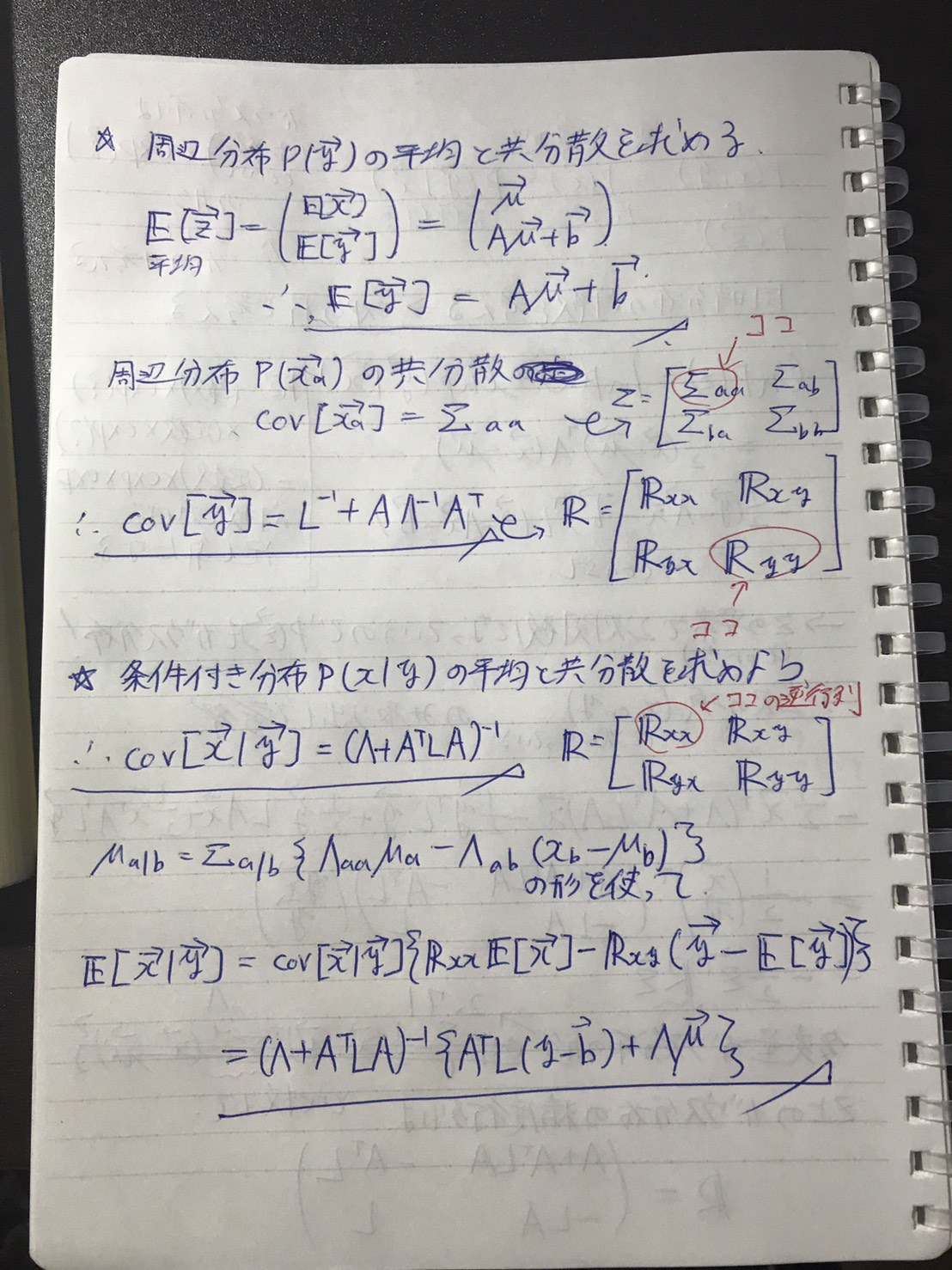2.3.1 条件付きガウス分布
ここで学びたいこと
多変量ガウス分布の性質
- 2つの変数集合$\vec{x_a}$,$\vec{x_b}$の同時分布がガウス分布に従うなら、もう一方の集合の条件付き分布もガウス分布になる。
→ 一方の変数（データ）集合$\vec{x_b}$を与えたときの条件付き分布$p(\vec{x_a}| \vec{x_b})$はガウス分布になる
今回はこれを証明するためにひたすら計算していく
2.3.1 条件付き分布を考えていく
覚えていますか？条件付き確率
p(\vec{x_a}| \vec{x_b})=\frac{p(\vec{x_a}, \vec{x_b})}{p(\vec{x_b})}
$\vec{x_b}$は与えられるデータなので、上記の式は$\vec{x_a}$と考える
以下の手順で進めていく。
①条件付き分布$p(\vec{x_a}| \vec{x_b})$がガウス分布だと示すために、同時分布のガウス分布の指数部を見る
②$\vec{\mu_{a|b}}, \vec{\Sigma_{a|b}}$を求めていく
①からやっていきます。
p(\vec{x}| \vec{\mu}, \Sigma) \propto \exp\left(-\frac{1}{2} (\vec{x} - \vec{\mu})^{\top} \Sigma^{-1} (\vec{x} - \vec{\mu}) \right)
多変量ガウス分布は定数 × exp(多変数の二次関数)の形をしている。
前につく定数がどうであれ、指数部をみればガウス分布かどうかわかる！！
前提として
多変量ガウス分布に従う$\vec{x}$がある。D次元。
条件付き分布の場合を考える
次元を分割して考える。互いに素で分ける
$\vec{x_a}$は最初のM次元分の要素。
$\vec{x_b}$は残りのD-M次元分の要素。
\begin{align}
\vec{x} = \left[ \begin{array}{c} \vec{x_a} \\ \vec{x_b} \end{array} \right]
\end{align}
$\vec{\mu}$についても分解
\begin{align}
\vec{\mu} = \left[ \begin{array} \\ \vec{\mu_a} \\ \vec{\mu_b} \end{array} \right]
\end{align}
共分散行列に関しても同様に
\vec{\Sigma} =\left[ \begin{array}\vec{\Sigma_{aa}} &\vec{\Sigma_{ba}} \\
\vec{\Sigma_{ab}} &\vec{\Sigma_{bb}} \end{array} \right]
これらを多変量ガウス分布の指数部に代入して計算
$\vec{x_a}$の関数としてみると二次形式になっている
→「多変量ガウス分布は定数 × exp(多変数の二次関数)の形をしている。」より、ガウス分布の形をとっている。
→①条件付き分布$p(\vec{x_a}| \vec{x_b})$はガウス分布である。
②$\vec{\mu_{a|b}}, \vec{\Sigma_{a|b}}$を求めていく
②$\vec{\mu_{a|b}}, \vec{\Sigma_{a|b}}$を求めていく
まず平方完成して係数部分を比較することで導く。
しかし、$\Lambda_{aa}$、$\Lambda_{ab}$ってナンゾ？
ラムダをシグマで表す
シューア補行列を使ってラムダをシグマであらわしたい！
2.3.1のまとめ！
- 2つの変数集合$\vec{x_a}$,$\vec{x_b}$の同時分布がガウス分布に従うなら、もう一方の集合の条件付き分布もガウス分布になる。 → 一方の変数（データ）集合$\vec{x_b}$を与えたときの条件付き分布$p(\vec{x_a}| \vec{x_b})$はガウス分布になる また、平均と共分散は2.81 2.82で表される
2.3.2 周辺ガウス分布
ここで学びたいこと
- $\vec{x_a}$、$\vec{x_b}$どちらの変数集合の周辺分布も同様にガウス分布になる
- 条件分布はガウス分布になることが分かったので、次は周辺分布を調べたい！
調べていく
先ほどと同じような手順で行う。
①同時分布の$\vec{x_b}$を見る
②$\vec{x_b}$についてまとめる
③同じように周辺分布の平均、共分散を求める
①同時分布のx_bを見る
2.84の第一項はガウス分布の標準的な二次形式に一致する。
②$\vec{x_b}$についてまとめる
周辺分布を導くために積分する
③同じように周辺分布の平均、共分散を求める
2.3.1と同じように比較方式で平均と共分散を求める
2.3.2のまとめ
周辺分布の平均・共分散は非常に簡潔に表現される！
2.3.3 ガウス変数に対するベイズの定理
ここで学びたいこと
- 今まで同時分布$p(x, y)$がガウス分布だった時に条件付き分布$p(y | x)$、周辺分布$p(x)$がどのようになるか計算してきた
- ①今回は、条件付き分布、周辺分布がガウス分布だったときに同時分布がどのようになるか見ていく（確率の乗法定理によると、$p(x, y)$=$p(x | y)$x$p(x)$）
- ②その後に、その結果を用いて$p(y)$, $p(x | y)$を求める
①これまでと同じように平均ベクトルと分散共分散行列を計算していく
周辺分布と条件付き分布をそれぞれ
p(\vec{x})=N(\vec{x}|\vec{\mu}, \Lambda^{-1})
p(\vec{y}|\vec{x})=N(\vec{y} | \vec{A} \vec{\x}+\vec{b}, {L^{-1}})
とする
求めたい分布を
\begin{align}
\vec{z} = \left[ \begin{array}{c} \vec{x} \\ \vec{y} \end{array} \right]
\end{align}
とおいて$p(z)$を計算していく
②その後に、その結果を用いて$p(y)$, $p(y | x)$を求める
Fin!
2.3.3のまとめ
数式のまとめはPRMLp90に。
なにが嬉しいの？
- 我々は変数yが観測されれば、条件付き分布$p(x | y)$を用いてx上での事後分布を表せるようになった！
P(X|Y)=\dfrac{P(X)P(Y|X)}{P(Y)}
log
互いに素
互いの最大公約数が１
http://mathtrain.jp/tagainiso
積分消去