Pong Game
Hardware Description Language Advent Calendar 2023 の第11目です。今回強化学習を目的とし、最初のステップとしてレトロビデオゲームを開発しました。CNNの回路は大規模と予想するため、ゲーム自体は単純なPongとしました。
PongゲームをYoutubeで探すと図1のような動画が見つかりました。
これを参考にしつつ、bsvによりプログラミングを行います。
強化学習の題材としてのPong
機械学習のうち、教師無し学習の一種に強化学習があります。例えばゲームを実行させ、行動の結果に報酬を与えることで、その行動を強化するものです。Pongゲームはボールをパドルで打ち合い、ボールをパドルで打ちそこなえば相手が得点するゲームです。従って、できる限り長くボールをパドルで打ち返し続けると報酬を与えるようにします。
BSV
言語はBSV (Bluespec System Verilog)を採用しました。ChatGPTにC/C++とBSVの利点欠点について比較してもらいましたが、C/C++の利点は過去資産が使える一方で、欠点はハードウエア設計にはあまり向かないのとのことでした。
一方で、BSVはプロセッサ回路、キャッシュコントローラ回路等様々な回路を構成するのに向いており、欠点としてはドキュメントやユーザベースなどの環境とのことでした。
それぞれ一長一短ありますが、BSVはその強力な自動FSM合成により、Cにおける条件文やループ文、関数に至るまでFSM(ステートマシン)に合成されます。そのためC/C++の利点が大幅に減少する結果となります(ChatGPT調べ)。
移植例を以下のコードに示します。これは3の倍数でアホになってそれ以外では値を集積するという例のための例のコードです。
C:
int i, a;
a = 0;
for (i = 1; i <= 10; i++) {
if (i % 3 == 0) printf("%d aho\n", i);
else a += i;
}
printf("a = %d\n", a);
BSV:
Reg#(int) i <- mkRegU,
a <- mkRegU;
a <= 0;
for (i <= 1; i <= 10; i <= i + 1) seq
if (i % 3 == 0) $display("%0d aho", i);
else a <= a + i;
endseq
$display("a = %0d", a);
そもそもverilogなので、verilog由来の非互換性である++演算子が無い、代入=を<=と記述、printf()を$display()と記述等のような書き換えは必要ですが、この例のようにwhile, for, if等の複雑なシーケンスを持つアルゴリズム部分をそのまま移植することが可能です。
特に、BSVで書いたコードをVerilogに変換可能なBSVコンパイラのbscが最近オープンソースとなったため、誰でも自由に利用可能です。
BSVをより深く知るためには
残念ながら日本語のサイトはほとんどありませんし、英語のサイトも情報がふんだんにあるとはいえません。これはユーザベースの少なさが原因でしょう。開発元のBluespecはこの言語環境を広めようと販売していましたが、思わしくなかったのかRISC-VのIPプロバイダに転向しました。その一方で我々にとっての福音は、ツールビジネスをやめたのでコンパイラがオープンソース化されたことです。
これは正しい戦略だと考えられます。現状のように、無償でさえユーザベースが広がりにくい言語障壁のため、ツールが有償であってはそれを乗り越えることは不可能だと思われます。
以下に参考となるポインタを示します。
- Bluespec⇒本家、ただしRISC-V情報のみ
- bsc⇒BSVコンパイラ
- BSVチュートリアル⇒Bluespec CTOによるチュートリアル
- Cybernet⇒BSVの特徴
- BSV (Bluespec SystemVerilog)によるスペースインベーダーの再設計
- BSVを用いたサウンドFSMのシーケンスベースによる再設計
- FS Microの記事
Cmod A7
FPGAボードは図2のCmod A7を選びました。これはDigilentから販売されているArtix 7シリーズのFPGAの評価ボードで、その特長は小さくてUSD 99と安価なことにあります。
CmodA7toPMODボードの設計
しかしながらArty A7ボードがPMODインタフェースを4個搭載しておりそのままPMOD-VGAやPMOD-Audioボードを接続できるのに対し、このボードはPMODが足りず画面が出ません。従って拡張PMODインタフェースボードを設計する必要があります。
拡張ボードはCmodA7toPMODと名付けました。ボード上に
- Cmod A7 FPGAボード
- PMODピンソケットコネクタ x 4
- ACアダプタコネクタ(MJ-179PH)
- 5V-3.3V電圧降下コンバータ(NJU7223F33)
- パドル用ピンソケット
等の部品を搭載します。
基本的にはFPGAの端子が多数出ているので、それに対してPMODインタフェースを接続するだけです。しかしながらソケット多段に信号を通すとノイズが大きくなるため、バッファICを入れました。
パドルコントロール
Pongの実装でパドルコントロールのためのツマミが必要となります。これはアナログ信号であり可変抵抗器で実装します。幸いCmodA7には2chのアナログ入力があるので、単純に可変抵抗器を接続すればOKです。
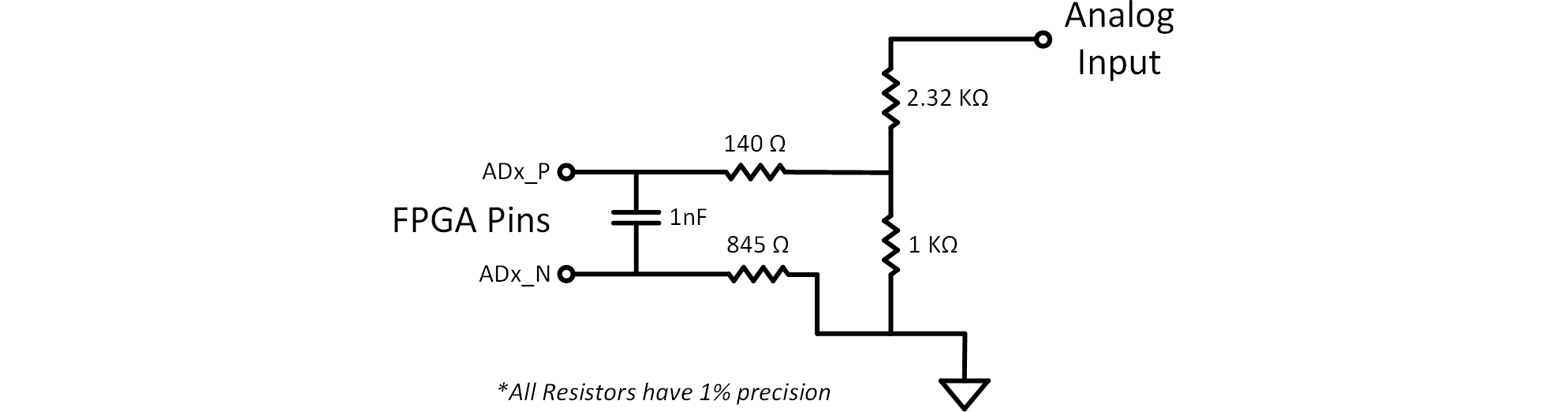
FPGAボード内のアナログ入力は図3のとおりです。外部の0~3.3Vの電圧を抵抗で分圧し、FPGAのADC入力を0~1Vの範囲に制限しています。
可変抵抗器及び直列の固定抵抗値を決定するため、アナログ回路シミュレータであるLTSpiceを使用しました。Spiceシミュレーションにより、固定抵抗10KΩを付けた場合の図3のADCへの入力電圧は0.20~0.94Vとなりました。
CmodA7toPMODボード回路
図4にCmodA7toPMODボード回路回路図を示します。
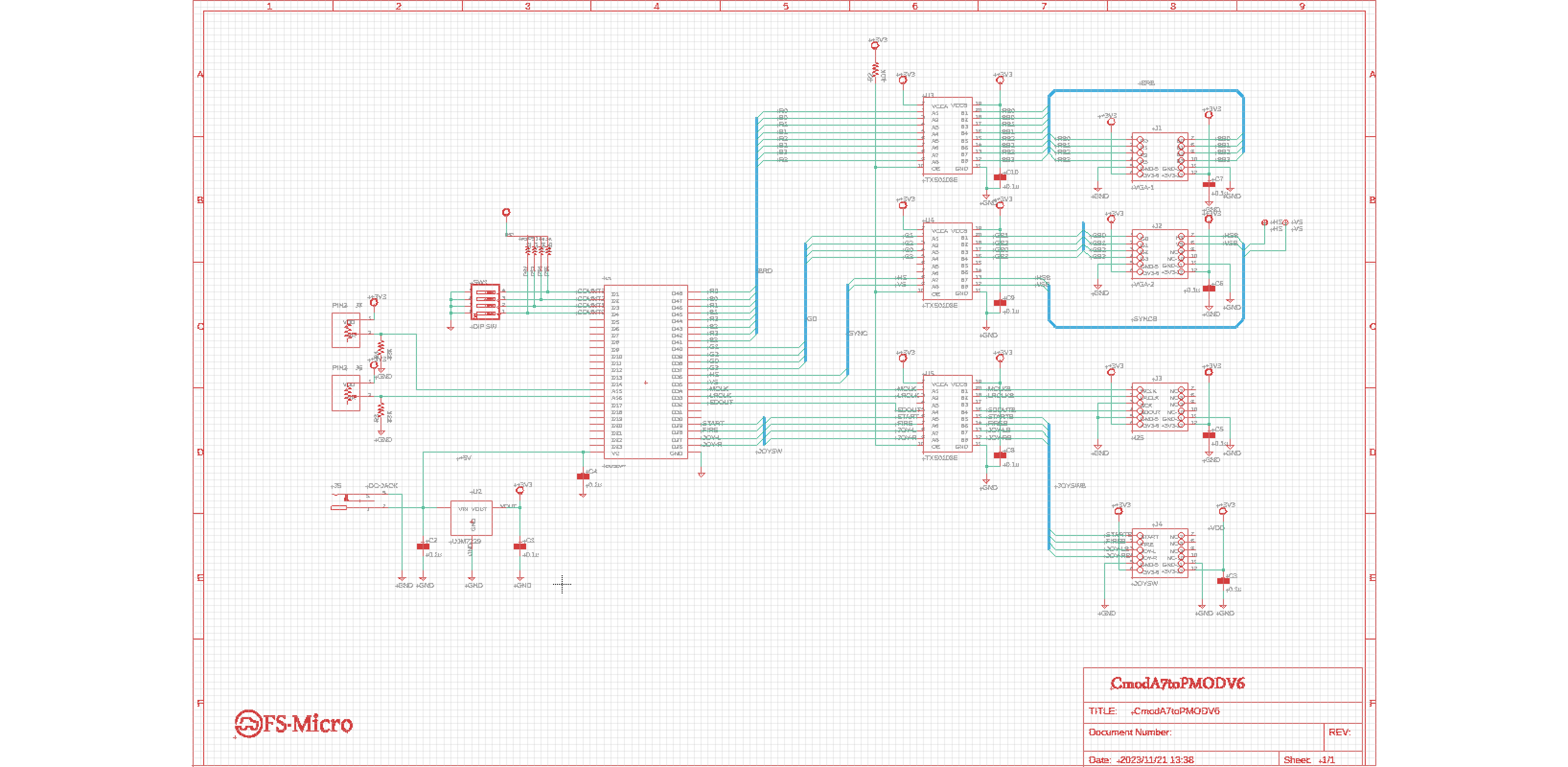
図4 CmodA7toPMODV6ボード回路図
PCBAは格安のJLCPCBに依頼しました。約20 USDで実装及び部品代込みです。

図5 Gerber図
図6に部品を実装したCmodA7toPMODボードを示します。
FPGA内部ブロック図
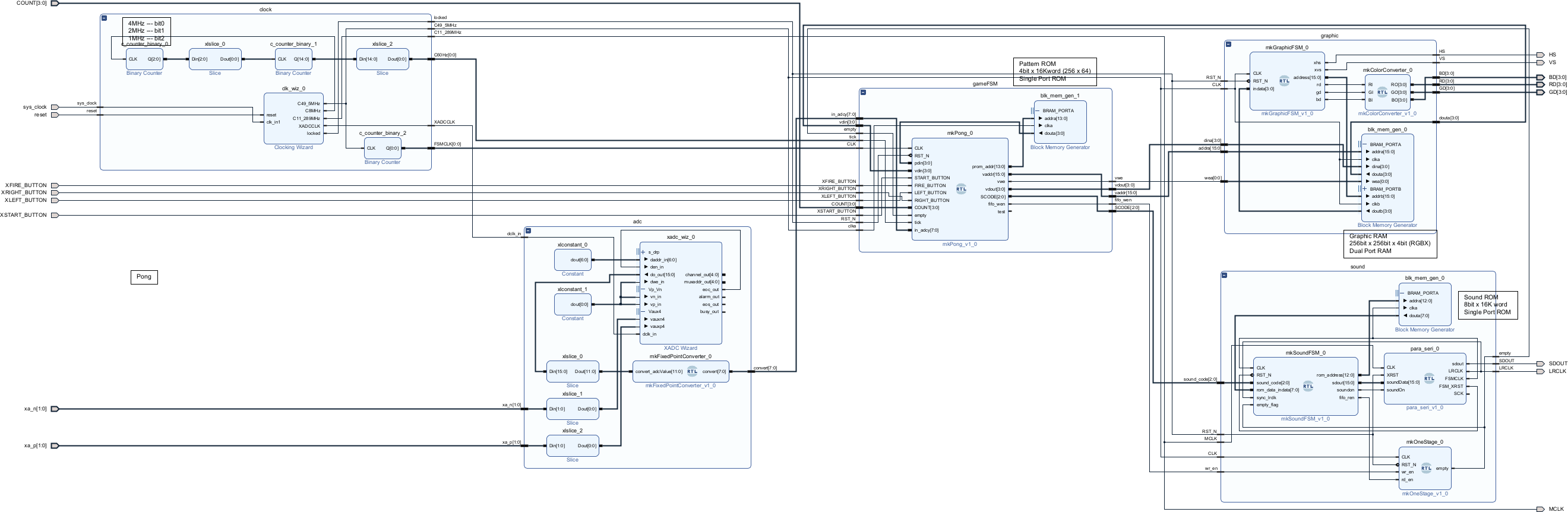
図7にPongのFPGA内部ブロック図を示します。左からクロックサブシステム、ADCサブシステム、ゲームサブシステム、上に行ってグラフィックサブシステム、下に行ってサウンドサブシステムから構成されます。
これらのモジュールのうち、クロックサブシステム、グラフィックサブシステム、サウンドサブシステムはほぼ過去部品の流用で、新規設計はゲームサブシステムとADCサブシステムのみです。以下に各サブシステムについて説明を記します。
グラフィックサブシステム
基本的には過去記事のとおりであり、SVGAのタイミング信号を発生します。他にはゲームサブシステムと共用するデュアルポートRAMがあります。さらに今回赤、緑、青のような原色ではなくレトロな中間色を出すための色変換回路を設けています。
ゲームサブシステム
新規設計の回路です。過去にインベーダーゲームを開発したようにFSMをBSVで書いていきます。BSVのFSMライブラリは非常に強力であり、whileやifが使えるので、ステート分解をせずにそのまま処理を書いていけば、bscがそれをステートマシンに変換してくれます。
メインループにおいて、
- ボールの動きと壁やパドルに対する衝突判定
- 左パドル:ボールに追従(たまにミス)
- 右パドル:ADC値による動き
- アウトの場合の得点の表示
を順に呼び出します。煩雑になるためボール制御のコードは示しませんが、基本的にif文の塊であり、壁の座標やボールが次に移動する先の空間の値の読み取りによる衝突判定等です。その他、跳ね返ったときのベクトルの反転等を扱います。ボールが右や左の端からこぼれた場合の処理も行います。
以下にメインループのコードを示します。
Stmt main = seq
initialize;
while (True) seq
ball_motion;
paddle_motion;
if (counter <= 4)
wait_timer(`TICK_WAIT4);
else if (counter <= 8)
wait_timer(`TICK_WAIT3);
else
wait_timer(`TICK_WAIT2);
endseq // while (True)
endseq;
mkAutoFSM(main);
ball_motionやpaddle_motionのように、BSVでは処理をまとめてシーケンスとして返す関数を持つことができます。このコードではcounter変数をボールがパドルで跳ね返るたびに+1しています。これによりボールはパドルで4回跳ね返る毎に速くなります。
最後の行のmkAutoFSM()はシーケンス定義を自動FSM合成関数に渡しているもので、合成結果はverilogのステートマシンとなります。関数は基本的にインライン化され、1stepを1 clockで実行します。もちろんハードウエアなので同時並行処理も書け、その場合はseq-endseqではなくaction-endactionで記述します。
BSVでは本来、ある論理が発火することを意味するrule文で書くことを基本としていますが、考え方を変える必要がある点は非常にハードルが高いと思われます。一方で私が気に入っているのはこの自動FSM合成で、実はruleはほとんど書いたことがありません。
ボール方向制御
コンピュータ側のパドルの縦位置はボールと同じにしてあるため、必ずボールを打ち返します。パドルでの跳ね返りは表1のとおり。
表1 2種類の乱数とボールの方向
| 乱数1 | bcount | 乱数2 | dy |
|---|---|---|---|
| 0 | 0 (45°) | 0 | (dx=1に対して)+1 |
| 1 | (dx=1に対して)-1 | ||
| 1 | 3 (18.4°) | 0 | (dx=3に対して)+1 |
| 1 | (dx=3に対して)-1 |
乱数1で傾きの逆数であるbcountを0または3とします。乱数2で方向がプラス+1かマイナスかを決定します。合わせると、bcount=0は右方向の場合速度ベクトルが(+1, +1)または(+1, -1)です。bcount=3の場合速度ベクトルが(+1, +1/3)または(+1, -1/3)です。
上下の壁にボールが衝突するとy方向の速度dyの符号を反転させます。一方、左右のパドルに衝突するとx方向の速度であるdxの符号を反転させ、かつ上記の表により方向をランダムに変化させます。
ボール動作
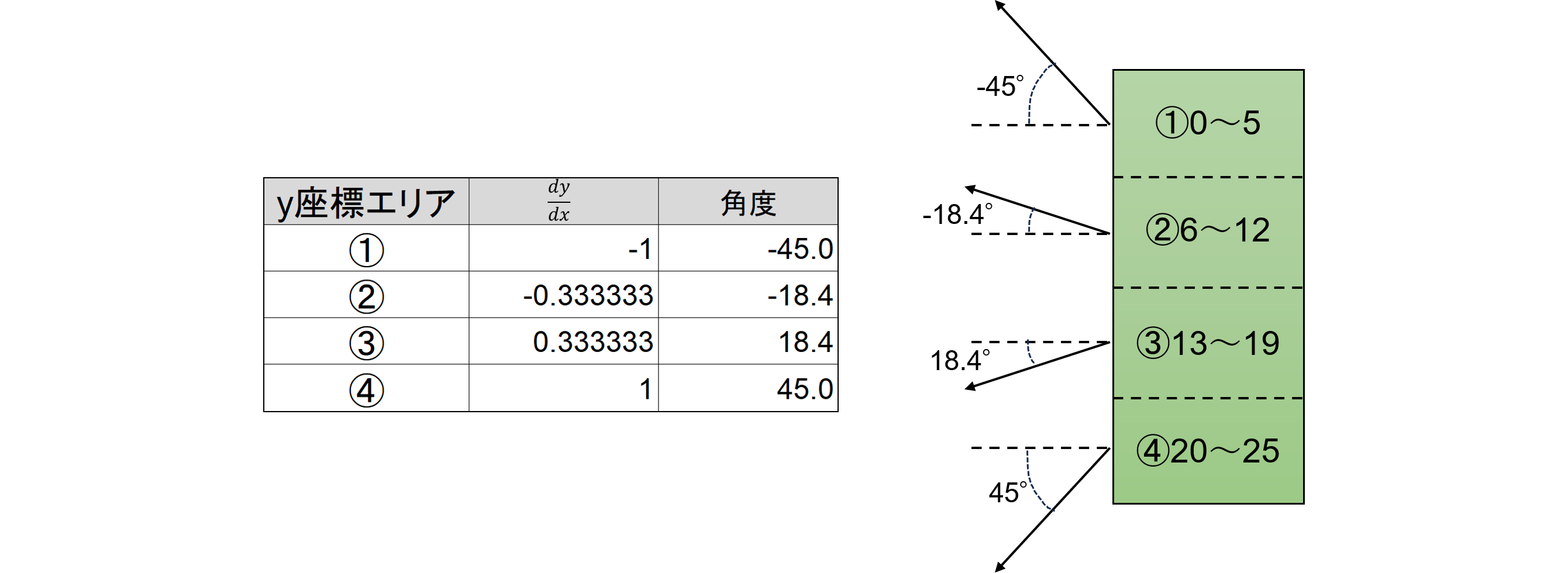
ボールが人間側パドルと衝突する判定は、ボール座標のVRAMデータを読み出して行います。右パドルのVRAMデータは3であるため、移動のたびにボール座標を読み出し3であれば衝突と判断します。
パドルのy相対座標範囲は+0~25であり、これを①0~5,②6~12、③13~19、④20~25の4領域に分割します。①に衝突した場合は-45°の角度で跳ね返り、②は約-18.4°の角度で跳ね返ります。これをxとyの増分であるdx, dyに変換すれば、-45度の場合はdx=1, dy=-1であり、-18.4度の場合はdx=3, dy=-1です。
ボール制御BSVコード
アルゴリズムとしては上記のようにボールの情報と対象物の情報を比較してある時点での動作を決めます。BSVはCのように構造体を持つことができます。様々なボールのプロパティを固めて保持することができます。例えば以下のコードに示すように、ボールスピード(x成分、y成分)、x座標、y座標等です。また、情報を取り出すにはCと同じようにドット.で連結して取得するところも同じです。
typedef struct {
Int#(8) dx;
Int#(8) dy;
} SpeedVector_t deriving(Bits, Eq);
typedef struct {
SpeedVector_t speedV;
UInt#(8) bcount;
UInt#(8) x;
UInt#(8) y;
} BallStatus_t deriving(Bits, Eq);
このようにstructやunion等の複雑なデータ構造が使用できるところもBSVの利点です。
サウンドサブシステム
強化学習本来の目的ではサウンドは不要ですが、ゲームとしても使用するためにサウンド機能を実装します。過去記事においてサウンドコントローラサブシステムは開発済みなので、サウンドの収集を行います。
Windows+Gによりゲームバーを呼び出し上記動画の動画をキャプチャします。次にffmpegによりwaveに変換します。これをaudacityによりカットして以下の4つのサウンドを取得します。
表2 4種のサウンド
| コード | 種類 |
|---|---|
| 1 | 発射音 |
| 2 | パドル |
| 3 | 壁 |
| 4 | アウト |
切り出した音声ファイルのサイズからROMの構成表を作成すると、表3のようなエントリポイントが得られます。
表3 ROM構成表
| Code | Sound | Start | Size [bytes] | Entry=Start+16 |
|---|---|---|---|---|
| 1 | 発射音 | 0 | 1,610 | 0+16 |
| 2 | パドル | 1,610 | 900 | 1,610+16 |
| 3 | 壁 | 1,610+900 | 872 | (1,610+900)+16 |
| 4 | アウト | 1,610+900+872 | 4,388 | (1,610+900+872)+16 |
| 合計 [bytes] (16KB ROM使用率) | 7,770 (95%) | |||
サウンドステートマシン
サウンドステートマシンは基本的に、ゲームを司るFSMから表2に示すコードを受け取り、それに従った音を鳴らします。音はwave形式でROMに格納されているので、そのデータ構造を解析するFSMを設計します。
以下にBSVのソースコードを示します。
// 波形ファイルを読み込み、オーディオDACにサウンドデータを出力するFSMの定義
import StmtFSM.*; // FSMを生成するためのユーティリティモジュールのインポート
// サウンドイベントと無音を表すマクロ定義
`define SOUND1 1 // 発射音
`define SOUND2 2 // パドルとの衝突音
`define SOUND3 3 // 壁との衝突音
`define SOUND4 4 // アウトの際の音
`define NULL 'h80 // 無音を表す値(8ビットPCMで中間値)
// 必要な型定義
typedef UInt#(13) Addr_t; // メモリアドレス用の13ビット符号なし整数
typedef UInt#(8) Data_t; // 8ビットデータ用の符号なし整数
typedef Bit#(16) Sound_t; // 16ビット符号付PCMサウンドデータ
typedef Bit#(3) Code_t; // サウンドコード
// FSMのインターフェース定義。外部からアクセスするためのメソッドが定義されています。
interface FSM_ifc;
method Action sound(Code_t code); // 音声コードを示す入力メソッド
method Action rom_data(Data_t indata); // ROMからのデータ入力メソッド
method Action sync(Bool lrclk); // 同期信号を処理するための入力メソッド
method Action empty(Bool flag); // FIFOが空を表す入力メソッド
method Addr_t rom_address(); // 現在のROMアドレスの出力メソッド
method Sound_t sdout(); // 音声出力データの出力メソッド
method Bool soundon(); // 音声が再生中かどうかを示す出力メソッド
method Bool fifo_ren(); // FIFOの読み出し要求の出力メソッド
endinterface
(* synthesize,always_ready,always_enabled *)
module mkSoundFSM(FSM_ifc);
// 内部ワイヤとレジスタの定義
Wire#(Code_t) code <- mkWire, // コードを格納するワイヤと現在のコードを保持するレジスタ
current <- mkRegU;
Wire#(Bool) lrclk <- mkWire; // 左右のクロック同期用のワイヤ
Reg#(Data_t) romdata <- mkRegU; // ROMから読み込まれたデータを保持するレジスタ
Reg#(Data_t) dout <- mkReg(`NULL); // データ出力用のレジスタ(初期値は無音)
Reg#(UInt#(32)) workd <- mkRegU; // 32ビット作業用データレジスタ
Reg#(UInt#(13)) dcount <- mkRegU; // 再生カウント用の13ビットレジスタ
Reg#(Addr_t) worka <- mkRegU, // アドレス計算用の作業用アドレスレジスタ
romaddr <- mkRegU, // ROMのアドレスレジスタ
addr <- mkRegU; // 出力用アドレスレジスタ
Reg#(UInt#(8)) ii <- mkReg(0); // ループカウンタ用の8ビットレジスタ
Reg#(Bool) son <- mkReg(False), // サウンド再生中フラグ用のレジスタ
sonEarly <- mkReg(False), // 早期サウンド開始フラグ用のレジスタ
ren <- mkReg(False), // FIFO読み込み要求フラグ用のレジスタ
emptyf <- mkReg(True); // FIFOが空かどうかを示すフラグ用のレジスタ
// subfunctions
// READ MEM サブ関数:メモリからの読み出し
// input: worka
// output: romdata;
//
function Stmt readmem;
return (seq
addr <= worka;
delay(2);
endseq);
endfunction
// READ COUNT サブ関数:カウント読み出し
// input: romaddr
// output: (romaddr,...,romaddr+3) => dcount;
// romaddr + 4 => romaddr;
//
function Stmt readcount;
return (seq
workd <= 0;
for (ii <= 0; ii <= 3; ii <= ii + 1) seq
worka <= romaddr + extend(3-ii);
readmem;
if (ii == 3) dcount <= truncate(workd<<8) | extend(romdata);
else workd <= workd<<8 | extend(romdata);
endseq
romaddr <= romaddr + 4;
endseq);
endfunction
// Mainloop メインループの定義
//
Stmt main = seq
while(True) seq
action
dout <= `NULL;
sonEarly <= False;
son <= False;
ren <= False;
endaction
await(!emptyf);
action
ren <= True; // consume 1 entry of Q
current <= code;
endaction
await(emptyf);
ren <= False;
// Sync to LRCLK
//
await(lrclk);
await(!lrclk);
delay(4);
// Format decoding
//
action
case (current)
`SOUND1: romaddr <= 0 + 16;
`SOUND2: romaddr <= 1610 + 16;
`SOUND3: romaddr <= (1610 + 900) + 16;
`SOUND4: romaddr <= (1610 + 900 + 872) +16;
endcase
endaction
readcount;
romaddr <= romaddr + extend(dcount) + 4;
readcount;
romaddr <= romaddr - 1;
// play loop
while (dcount != 0) seq
// Play 0
if (sonEarly == False) seq
// 1cycle目
readmem;
action
sonEarly <= True;
son <= False;
dout <= `NULL;
endaction
endseq else seq
// 2cycle目以降
readmem;
action
son <= True;
dout <= romdata;
endaction
endseq // if
delay(11);
action
romaddr <= romaddr + 1;
worka <= romaddr + 1;
dcount <= dcount - 1;
endaction
endseq // while(!終了条件)
endseq // while(True)
endseq; // Stmt
mkAutoFSM(main); // FSMを生成し実行
method Action sound(Code_t incode);
code <= incode;
endmethod
method Action rom_data(Data_t indata);
romdata <= indata;
endmethod
method Addr_t rom_address();
return addr;
endmethod
method Sound_t sdout();
let bdout = pack(dout); // 現在のオーディオデータ(dout)をパックし、16ビットのデータ(bdout)に変換します。
let s = ~bdout[7]; // 8ビット目(MSB)を反転させてサインビット(s)を生成します。
return {{s,s},bdout[6:0],{7'h0}}; // オーディオデータをsignedに変換します。
endmethod
method Bool soundon();
return son;
endmethod
method Action sync(Bool inlrclk);
lrclk <= inlrclk;
endmethod
method Bool fifo_ren();
return ren;
endmethod
method Action empty(Bool flag);
emptyf <= flag;
endmethod
endmdule: mkSoundFSM
ADC
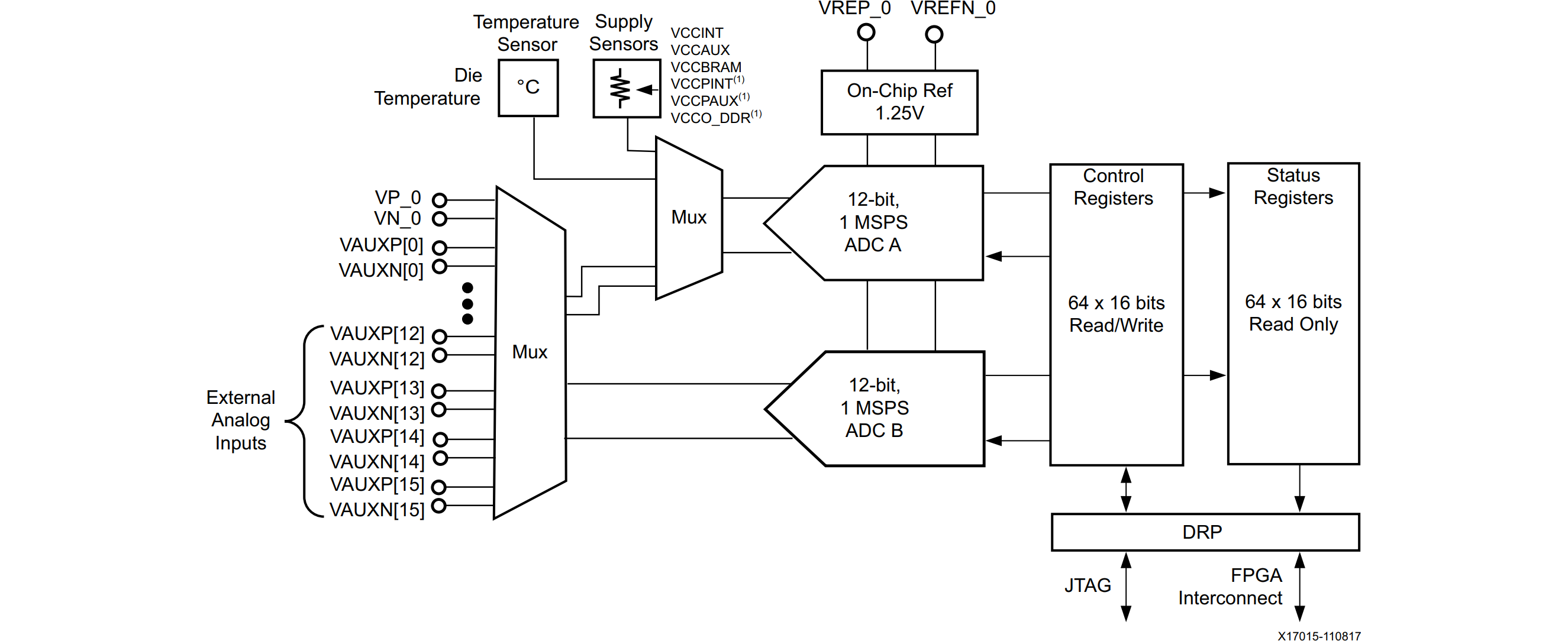
Artix 7シリーズFPGAのADCを利用するには様々な制約があります。ADCのユーザーズガイド(UG480)に書かれていますが、DRP(Dynamic Reconfigure Register)経由で読み出します。
図9にADCのブロック図を示しますが右下にDRPブロックがあります。
設計計算例
ADCから読みだした可変抵抗電圧の値をパドル座標に変換するためにはデータ変換が必要であり、その設計計算を行います。
ADC入力電圧は開始角$a$の値を$V_\text{a}$、終了角$a+b$の値を$V_\text{a+b}$として、$
\require{color}
\definecolor{pink}{rgb}{1.0,1.0,1.0}
$
- VRの全角度は300°
- VRの使用角はパラメータ化し、開始角a[°]、範囲b[°]
- VRの全角度の際のADC入力電圧はLTSpiceの結果より、0.2~0.94[V]
これらより、使用電圧は開始角の値を$V_\text{a}$、終了角の値を$V_\text{a+b}$として、
- $V_\text{L}=0.2$, $V_\text{H}=0.94$
- $V_\text{range}=V_\text{H}-V_\text{L}=0.74$
- $V_\text{a}=\frac{V_\text{range}}{300}a+V_\text{L}$
- $V_\text{a+b}=\frac{V_\text{range}}{300}(a+b)+V_\text{L}$
次にAD変換後のデータDは入力全範囲0~1[V]を4096分割する。開始角の値を$D_\text{a}$、終了角の値を$D_\text{a+b}$として
- $D_\text{a}=4096V_\text{a}=\frac{4096V_\text{range}}{300}a+4096V_\text{L}=10.1a+819.2$
- $D_\text{a+b}=4096V_\text{a+b}=10.1(a+b)+819.2$
- $D_\text{range}=10.1b$
一方、y座標の制約は以下のとおりであり、上限$y_\text{top}$と下限$y_\text{bottom}$の値でクリッピングが必要。
- $y_\text{bottom}=44$, $y_\text{top}=186$
- $y_\text{range}=y_\text{top}-y_\text{bottom}=142$
これらからy座標を求めると、ADCのデータを$D$とすれば、
- $y=\frac{y_\text{range}}{D_\text{range}}(D-D_\text{a})+y_\text{bottom}=\frac{142}{10.1b}D-\frac{142}{b}a-\frac{142\cdot 819.2}{10.1b}+44\
=\frac{224.9}{b\ll4}D-\frac{142}{b}a-\frac{11514}{b}+44=\frac{225D-2272a-184216}{b\ll4}+44$
y式中のシフトは固定小数点演算を行うために分母分子を16倍しているものです。さらに最小値$D_\text{a}$、最大値$D_\text{a+b}$で入力ADCデータのクリッピングを行います。
- $D_\text{a}=10.1a+819.2=(162a+13107)\gg4$
- $D_\text{a+b}=10.1(a+b)+819.2=(162(a+b)+13107)\gg4$
以上より、完成したBSVコードは以下のとおりです。
package FixedPointConverter;
import Vector::*; // ベクター操作のためのモジュール
interface ConverterIfc;
method Bit#(12) convert(Bit#(12) adcValue);
endinterface
// ADCの値から座標に変換する演算器(固定小数点演算を使用)
(* synthesize, always_ready, always_enabled, no_default_clock, fault_reset *)
module mkFixedPointConverter #(
parameter Bit#(12) a, // 角度の最小値
parameter Bit#(12) b // 角度範囲
) (ConverterIfc);
method Bit#(12) convert(Bit#(12) adcValue);
// パラメータの拡張
Bit#(20) extendedA = zeroExtend(a);
Bit#(20) extendedB = zeroExtend(b);
// 座標の下限と上限に対応するADC値の計算
Bit#(20) adcMinValue = (162 * extendedA + 13107) >>4; // Min = 10.1A + 819.2
Bit#(20) adcMaxValue = (162 * (extendedA + extendedB) + 13107) >> 4; // Max = 10.1(A+B) + 819.2
// クリッピング処理
Bit#(12) clippedAdcValue = (adcValue < truncate(adcMinValue)) ? truncate(adcMinValue) :
(adcValue > truncate(adcMaxValue)) ? truncate(adcMaxValue) :
adcValue;
Bit#(24) coordinate = ((zeroExtend(clippedAdcValue) * 225
- zeroExtend(extendedA) * 2272 - 184216)
/ zeroExtend(extendedB) >> 4) + 44;
return truncate(coordinate);
endmethod
endmodule
endpackage: FixedPointConverter
これは単なる組み合わせ回路なのでC/C++でも同様にできるかもしれませんが、設計計算の実例としてコードを示しました。
完成画面
システムが動作している画面を図10に示します。右パドルは人間が操作しています。
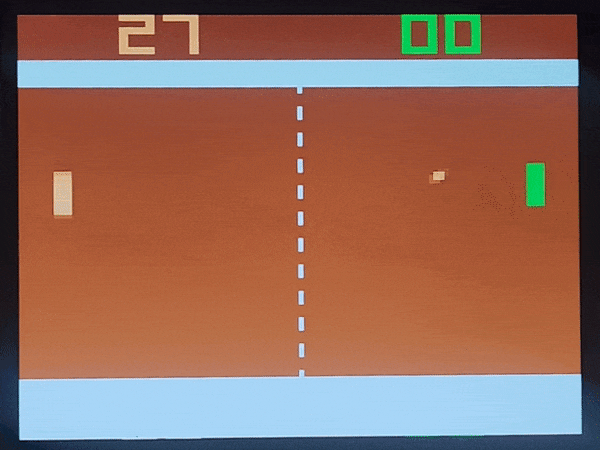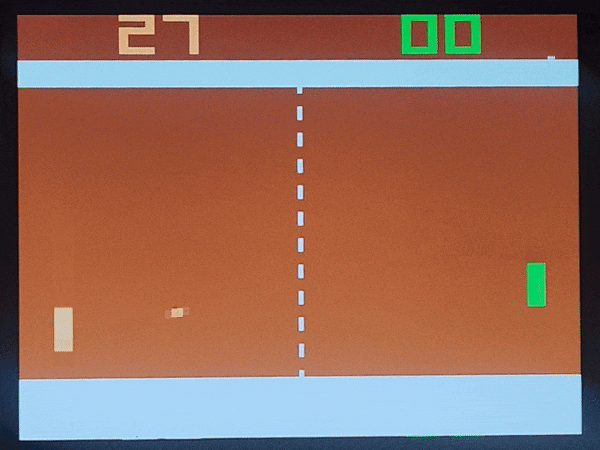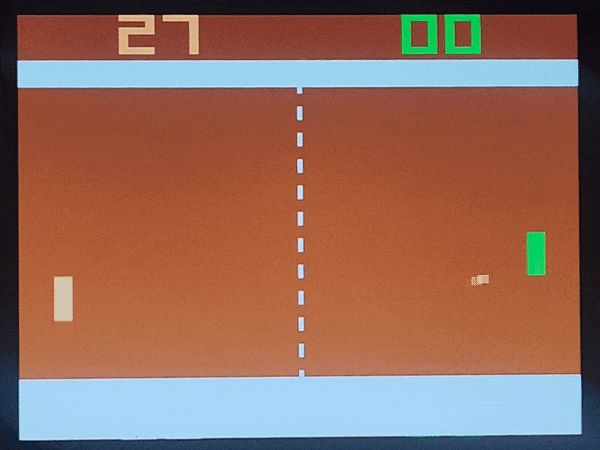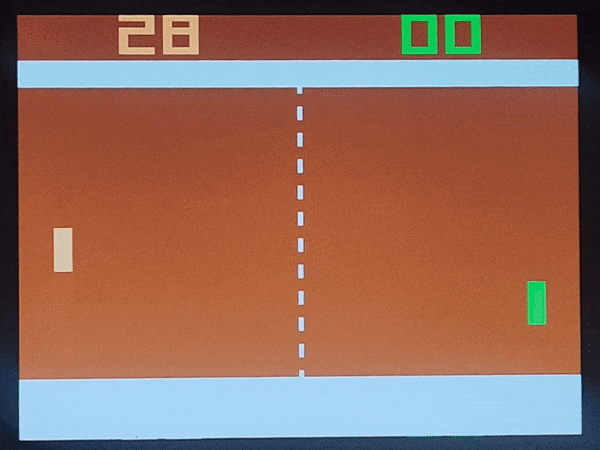
図10 Pong動作画面
今後の予定や感想
最初に書いたようにPongゲームの開発は、第2ステップとして、これを用いた強化学習を実装したいと思っています。
今回過去の資産を流用しながらBSVを用いて短期間で新規ゲームを開発しました。「巨人の肩に乗る」という英語由来のフレーズがありますが、まさにBSVは巨人であり新規開発がとても楽にできます。巨人の肩の高さまで登る苦労はあるものの、一旦登ってしまえばそこからは楽な道筋となります。もうverilogでステートマシンを苦労して書く必要はありません。
verilogで苦労するテストベンチはシーケンスを組みDUTに様々なデータを供給しますが、BSVではFSM生成ライブラリにより簡単に書くことができます。
BSVを大学教育に採用すれば日本の設計力が上がるのではないかと思いますが、海外の一部の大学でしか採用されていないようであり、日本の国力を考えると大変残念です。今後の国内でのBSVの普及が期待されます。