pytorchを使った線形回帰

初めに

pytorchは、自動微分で求まる傾きを使って誤差を最小化することで、ニューラルネットワークの重み(パラメタ)を最適化しているが、この動作を理解するために単純な例でやってみる。

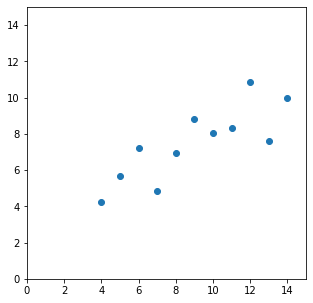
今回は、以下のようなデータに対して、$y=ax+b$の$a$と$b$を求める。

xi = np.array([10.0,  8.0, 13.0, 9.0 , 11.0, 14.0, 6.0 , 4.0, 12.0, 7.0, 5.0])
yi = np.array([8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68])

最小二乗法を使った場合

答え合わせのため、sklearnを使って、傾きと切片を求めておく

線形回帰

from sklearn import linear_model
clf = linear_model.LinearRegression()
clf.fit( xi.reshape(len(xi),1),yi )
print( f'傾き(a):{clf.coef_[0]:.5f} \n切片(b):{clf.intercept_:.5f}') 

実行結果

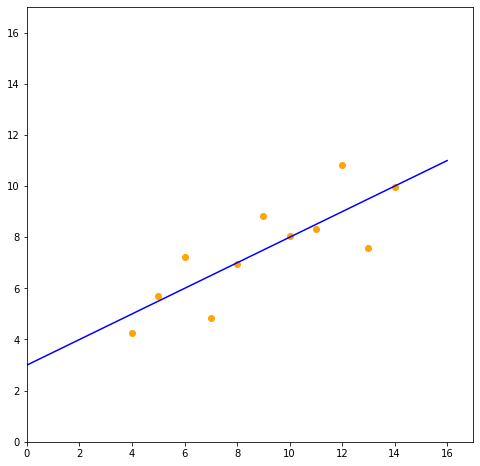
傾き(a):0.50009 
切片(b):3.00009

これを、pytorchで求められるかやってみる。

pytorchをつかった線形回帰

まず、今回使う変数を作る
求めるパラメータは(a,b)。初期値は乱数で初期化する

# 説明変数
xi = np.array([10.0,  8.0, 13.0, 9.0 , 11.0, 14.0, 6.0 , 4.0, 12.0, 7.0, 5.0])
# ラベル
yi = np.array([8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68])
a = np.random.rand()     # 傾き
b = np.random.rand()     # y切片

# pytorchで扱えるようにテンソルにする。
# 求めるパラメタ(A,B)は、後から微分計算するのでrequires_grad=Trueとする
Xi = torch.tensor( xi )  # 説明変数のテンソル
Yi = torch.tensor( yi )  # 目的変数
A = torch.tensor( a , requires_grad=True )
B = torch.tensor( b , requires_grad=True )

パラメタA,Bを使って、予測値:$Y=A*Xi+B$と、正解(教師データ):$Yi$との誤差(平均二乗誤差)を計算する。

# 予測値を計算
Y = A*Xi + B

# 正解ラベルとの誤差を計算(差を二乗したものの平均)
loss = torch.sum((Y-Yi)**2) / len(Y-Yi) 

# pytorchの関数を使って、以下としても同じ
mseloss  = torch.nn.MSELoss()
loss = mseloss( Y, Yi )

これ(loss)を最小とするA,Bを求めればよいことになる。

具体的には、lossをA,Bの関数として、A,Bそれぞれで偏微分したうえで、Xiでの傾きを計算する。(これにより、A,Bを微小変化させた際のlossがどう変化するか(増えるのか/減るのか)がわかる。)

pytorchでは、出力値:lossのbackward()を呼ぶと、計算グラフを使った自動微分で傾きが計算され、結果がA,Bのgradプロパティに格納される。
あとは、optimizer.step()を実行すると、この傾きを使ってA/Bが更新される。

optim = torch.optim.RMSprop([A,B], lr=0.001)

for i in range(6000):
    # A,Bの傾きがある場合はクリアしておく
    # (loss.backward()の傾き計算に、前の計算結果が影響してしまうので)
    if A.grad != None:
        A.grad.zero_()
    if B.grad != None:
        B.grad.zero_()

    Y = A*Xi + B

    # 誤差を計算(平均二乗誤差)    
    loss = torch.sum( (Y-Yi)**2 ) / len(Y-Yi)
    
    # 微分計算(A.grad、B.gradに傾きが設定される)
    loss.backward()

    # 計算された傾きを使って、A,Bを更新
    optim.step()

print( f'loss:{loss.detach().tolist():.5f}' )
print( f'A:{A.detach().tolist():.5f} \nB:{B.detach().tolist():.5f}' )

以下のコードでも同じ

optim = torch.optim.RMSprop([A,B], lr=0.001)
mseloss  = torch.nn.MSELoss()

for i in range(6000):
    optim.zero_grad()
    Y = A*Xi + B
    loss = mseloss( Y, Yi )
    loss.backward()
    optim.step()

print( f'loss:{loss.detach().tolist():.5f}' )
print( f'A:{A.detach().tolist():.5f} \nB:{B.detach().tolist():.5f}' )

実行結果

loss:1.25118
A:0.49959 
B:2.99959

skleanを使って求めた係数(傾き:0.5、y切片:3)と近い値が求まっていることがわかる。