Pythonでプログラミングを学習中に,ビュフォン(Buffon)の針のシミュレータを実装したのですが,そのときのアルゴリズムについてメモ。
ビュフォン(Buffon)の針とは
等間隔に並んだ直線の上に針をたくさん落とし,直線と交わっている針の割合をもとに円周率$\pi$を推定しようというものです。
今,直線の間隔$d$,針の長さを$l$とします。
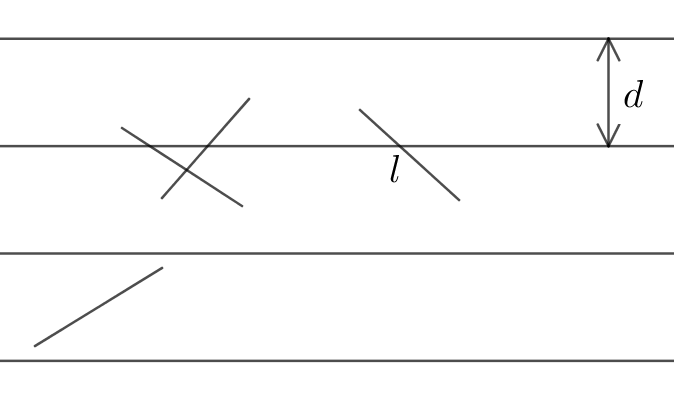
一般に$l \le d$のとき,針を落とした時に直線と交わる確率は$\frac{2l}{\pi d}$になることが知られています。よって針を$n$本落としたとき,直線と$m$本が交わったとすると,
$$\frac{m}{n} = \frac{2l}{\pi d}$$
と近似でき,このことから
$$ \pi = \frac{2nl}{md}$$と円周率が計算できます。
詳しくはWikipedia等を参照してください。
準備
さて,ビュフォンの針を実装していきます。BuffonCalというクラスにまとめます。
初期設定
import numpy as np
class BuffonCal:
def __init__(self, length, interval, width_x=1000, width_y=1000):
self.length = length
self.interval = interval
self.width_x = width_x
self.width_y = width_y
lengthが針の長さ$l$,intervalで直線の間隔$d$を表すことにします。
width_xとwidth_yは針を落とすキャンパスを記しています。
直線のy座標を返すメソッド
def base_lines(self):
self.lines = (i * self.interval
for i in range(self.width_y//self.interval + 1))
return self.lines
直線のy座標をイテレータの形で返します。
針を落とすメソッド
def drop(self, number):
self.number = number
self.drops_x1 = self.width_x * np.random.rand(self.number)
self.drops_y1 = self.width_y * np.random.rand(self.number)
theta = np.pi * np.random.rand(self.number)
self.drops_x2 = self.drops_x1 + self.length * np.cos(theta)
self.drops_y2 = self.drops_y1 + self.length * np.sin(theta)
針の端点の座標を$(x_1,y_1)$,$(x_2, y_2)$として,まず$(x_1,y_1)$を乱数で生成し,さらに偏角$\theta$を乱数で生成して$(x_2, y_2)$を決定しています。必ず$y_1 \le y_2 $になるようにしてあります。
各座標ごとにnumpy.ndarray型として格納しています。
落とした針のうち,直線と交わっている本数を数える
さて,落とした針のうち,直線と交わっている針の本数を数えていきましょう。最も素直なのは以下のプログラムでしょうか。
def count(self):
self.counts = 0
for y1, y2 in zip(self.drops_y1, self.drops_y2):
for line_y in self.base_lines():
if y1 <= line_y <= y2 :
count += 1
break
return self.counts
いわゆる総当たりプログラムで,針が線をまたいでいるとき,$y_1 \le (線のy座標) \le y_2$となる(線のy座標)が存在するので,そのようなものがあるかをfor文を用いて全探索しています(このプログラムを採用する場合はNumpyではなくリストを使ってください)。
それに対し,今回使ったプログラムは以下になります。
def count(self):
drops_y1_int = self.drops_y1 // self.interval
drops_y2_int = self.drops_y2 // self.interval
self.counts = len(np.where(drops_y1_int != drops_y2_int)[0])
return self.counts
2~3行目で,各$y1,y2$を直線の間隔$d$で割った商を求めています。
もし,針が直線と交差している場合,商は異なるはずだし,交差していない場合は同じ商になるはずなので,4行目で商が異なるものの数を計算しています。for文を回すより速いと思います。
ちなみに,Pythonの「//」は,割る数が小数であっても計算可能です。以下に例を挙げます。
>>> 5 // 2
2
>>> 5 // 2.1
2.0
>>> 7.4 // 0.9
8.0
残りの処理
$\pi$の推定値を返すコードも記載しておきます。
def pi_cal(self):
if self.counts > 0:
self.pi = (2*self.length*self.number) / (self.counts*self.interval)
else:
self.pi = float("inf")
return self.pi
def difference(self):
return '{:+}'.format(self.pi - np.pi)
終わりに
このプログラムは最終的にtkinterを使って,簡単なGUIアプリケーションにまとめました。コードはこちら。