測度論の「お気持ち」を最短で理解する

数学における「測度論(measure theory)・ルベーグ積分(Lebesgue integral)」の"お気持ち"の部分を，「名前は知ってるけど何なのかまでは知らない」という非数学科の方に向けて書いてみたいと思います．

インターネット上にある測度論の記事は，厳密な理論に踏み込んでいるものが多いように思います．本記事は出来るだけ平易で直感的な解説を目指します。厳密な定義を一切しませんので気をつけてください¹．

適宜，注釈に詳しい解説を載せます．

測度論によって積分の概念が広がる

測度論のメリットは主に積分の概念が広がり，より簡単・統一的に物事を扱えることにあります．まずは高校でも習う「いつもの積分」を考え，それをもとに積分の概念を広げていきましょう．

復習 いつもの積分(リーマン積分)

高校で習う積分は「リーマン積分(Riemann integral)」といいます．簡単に復習していきます．

長方形による面積近似

リーマン積分は，縦に分割した長方形によって面積を近似するのが基本です(区分求積法)。下の図を見るのが一番手っ取り早いでしょう．

区間 $[0, 1]$² を $n$ 等分し， $n$ 個の長方形の面積を求めることで，積分を近似しています。式で書くと，以下のようになります．
$$\int_0^1 f(x) , dx ; \approx ; \frac{1}{n} \sum_{k=0}^{n-1} f\left(\frac{k}{n}\right).$$

上の図では長方形の左端で近似しましたが，もちろん右端でも構いません．

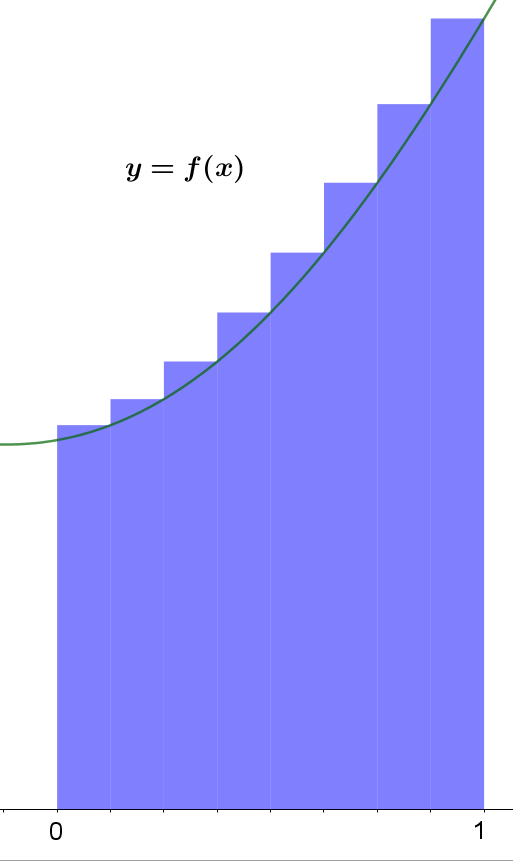
$$\int_0^1 f(x) , dx ; \approx ; \frac{1}{n} \sum_{k=1}^{n} f\left(\frac{k}{n}\right).$$

もっと言えば，面積の近似は長方形の左端や右端でなくても構いません．

ガタガタに見えますが，長方形の上の辺と $y=f(x)$ のグラフが交わっていればどこでも良いです．この近似を式にすると以下のようになります．

$$\int_0^1 f(x) , dx ; \approx ; \frac{1}{n} \sum_{k=1}^{n} f\left(a_k\right) \quad \left(\text{但し，}a_k\text{は}\quad\frac{k-1}{n}\le a_k \le \frac{k}{n}\text{を満たす数}\right).$$

余談 素朴なコード

プログラマであれば，一度は積分を求める(近似する)コードを書いたことがあるかもしれません．ここはQiitaなので，例を一つ載せておきましょう．一番最初に書いた，左側近似のコードを書いてみることにします^3．

integral.py

# python

f = lambda x: ###
n = ###

S = 0
for k in range(n):
    S += f(k/n) / n

print(S)

簡単ですね．

長方形近似の極限としてのリーマン積分

リーマン積分は，こうした長方形近似の極限として求められます(厳密な定義ではありません³)．
$$\int_0^1 f(x) , dx ; = ; \lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^{n} f\left(a_k\right) ;;\left(\frac{k-1}{n}\le a_k \le \frac{k}{n}\right) .$$
この式はすぐ後に使います．

リーマン積分できない関数

さて，リーマン積分を考えましたが，この考え方を用いて，区間 $[0,1]$ 上で定義される以下の関数 $1_\mathbb{Q}$⁴ の積分を考えることにしましょう．

1_\mathbb{Q}(x) = \left\{
\begin{array}{ll}
1 & (x \text{は有理数}) \\
0 & (x \text{は無理数})
\end{array}
\right.

区間 $[0,1]$ の中に有理数は無数に敷き詰められている(稠密といいます)ため，厳密な絵は描けませんが，大体イメージは上のような感じです．
「こんな関数，現実にはありえないでしょ」と思うかもしれませんが，数学の世界では放っておくわけにはいきません．

では，この関数をリーマン積分することを考えていきましょう．

リーマン積分できないことの確認

上で解説した通り，長方形近似を考えます．

区間 $[0,1]$ 上には有理数と無理数が稠密に敷き詰められている⁵ため，以下のような2つの近似が考えられることになります．
$$\lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^{n} 1_\mathbb{Q}\left(a_k\right) ;;\left(\frac{k-1}{n}\le a_k \le \frac{k}{n}, ; a_k\text{は有理数}\right) ,$$
$$\lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^{n} 1_\mathbb{Q}\left(a_k\right) ;;\left(\frac{k-1}{n}\le a_k \le \frac{k}{n}, ; a_k\text{は無理数}\right) .$$

ところが，$1_\mathbb{Q}$ の定義より，2式を計算すると上が $1$，下が $0$ になります．これは
$$\lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^{n} 1_\mathbb{Q}\left(a_k\right) ;;\left(\frac{k-1}{n}\le a_k \le \frac{k}{n}\right) $$
が一意に定まらず，収束しないことを意味しています．すなわち，この関数はリーマン積分できないのです．

積分の概念を広げよう~測度論の導入~

上で， $[0,1]$ 上で定義された $1_\mathbb{Q}$ という関数は，リーマン積分できないことを確認しました．しかし，この関数は後で定義する「ルベーグ積分」はできます．それでは，いよいよ測度を導入し，積分の概念を広げましょう．

測度とは"長さや面積の重みづけ"である

測度とは，簡単にいえば，長さや面積の「重み/尺度」を厳密に議論するための概念です⁶．

「面積の重み」とは，例えば以下のようなイメージです(重み付き和といえば多くの方が分かるかもしれません)．

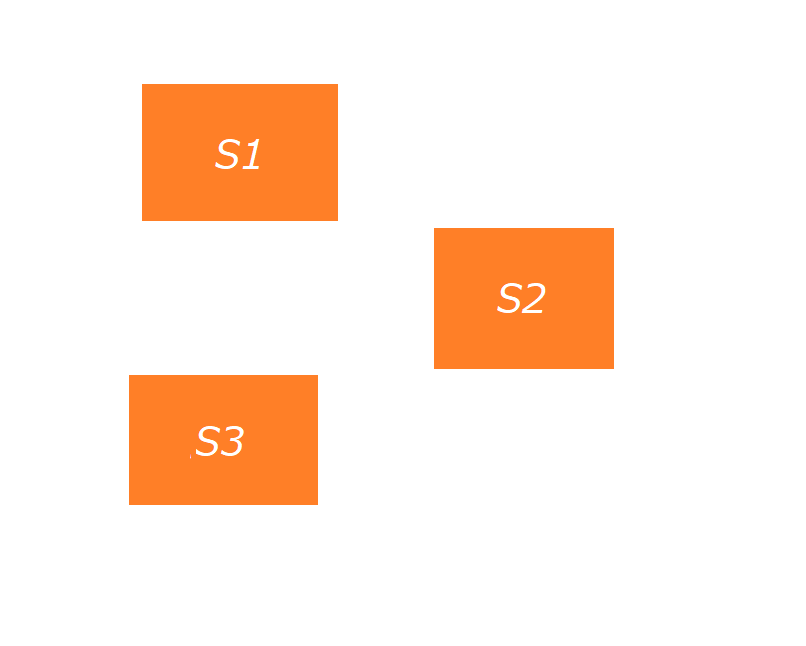
上の3つの長方形の面積和 $S$ を考えましょう．
まずは普通に面積の重み $1$ だと思うと，
$$ S ; = ; S_1 + S_2 + S_3 $$
ですね．一方，3つの面積の重みをそれぞれ $w_1, w_2, w_3 $ と思うと，
$$ S ; = ; w_1 S_1 + w_2 S_2 + w_3 S_3 $$
となります．
測度とは，ここでいう $w_i ; (i = 1, 2, 3)$ のことです⁷．

そして測度は，ちゃんと積分の概念が広がるような"性質の良いもの"であるとします．どのように性質が良いのかは本質的で重要ですが，少し難しいので注釈に書くことにします⁸．

追記：測度は集合自体の大きさを測るものといった方が正しいです．「長さや面積の重みづけ」と思って問題ありませんが，気になる方，逆につまづいた方は脚注8を参照してください．

議論を進めていきましょう．

ルベーグ測度

さて，測度とは「面積の重みづけ」だと言いました．ここからは，そんな測度の一種「ルベーグ測度」を考えていきましょう．ルベーグ測度とは，リーマン積分の概念を拡張するための測度で，リーマン積分の値そのままに，積分可能な関数を広げることができます．
さて以下では， $\int f(x) , dx$で， $f$ のルベーグ積分(ルベーグ測度を用いた積分)を表すことにします．本当はリーマン積分と記号を変えるべきですが，リーマン積分可能な関数は，ルベーグ積分しても同じ値になる⁹ので，慣習で同じ記号が使われます．

almost everywhere という考え方

面積の重みを定式化することで，「重みゼロ」という概念についても考えることができるようになります．重みゼロの部分はテキトーにいじっても全体の面積に影響を及ぼしません．

次の $ y = f(x) $ のグラフを見てください．

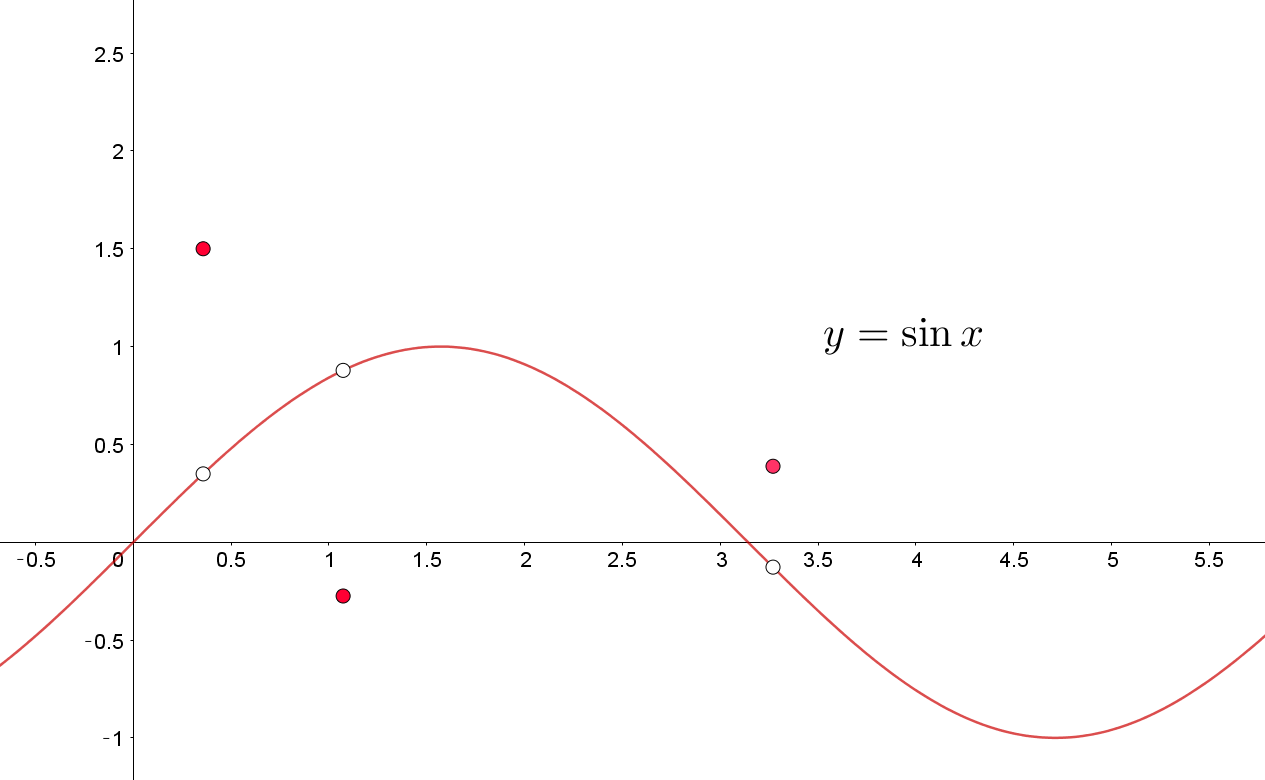
大体は $ y = \sin x$ のグラフですが，ちょっとだけ変な点があるのが分かります．

ただ，この点は面積の重みを持たず，積分に影響を及ぼさないことは容易に想像できるでしょう．このことを数学では，

• ほとんど至るところで $f(x) = \sin x .$
• $ f(x) = \sin x \quad almost ; everywhere. $
• $ f(x) = \sin x \quad a.e.$

などと記述します．重みゼロの点を変えても積分値に影響を及ぼしませんから，以下の事柄が成立します．

区間 $[a, b]$ 上で定義された関数 $f, g$ が $f = g ;; a.e.$ なら$$ \int_a^b f(x); dx = \int_a^b g(x) ; dx.$$

almost everywhere は，測度論の根幹をなす概念の一つです．

リーマン積分不可能だがルベーグ積分可能な関数

では，$1_\mathbb{Q}$ についてのルベーグ積分を考えてみましょう．

実は，無理数の数は有理数の数より圧倒的に多いことが知られています¹⁰．ルベーグ測度で測ると，有理数の集合には面積の重みが無いことがいえます¹¹．
すなわち，
$$ 1_\mathbb{Q} = 0 ;; almost ; everywhere $$
がいえるのです．
このことを用いて，$1_\mathbb{Q}$ はルベーグ積分することができます．
$$\int_0^1 1_\mathbb{Q}(x) , dx = \int_0^1 0 , dx = 0. $$
リーマン積分不可能だった関数が積分できました．積分の概念が広がりましたね．
一連の作業は，**"面積の重みをちゃんと考えることで，「変な関数」を「積分しやすい関数」に変形し，積分した"**といえます．必ずしも「変な関数」を「積分しやすい関数」にできる訳ではないですが，それでも，次節で紹介する積分の構成を用いて，積分値を考えます．

この拡張により，「積分できない関数は基本的にはなくなった」と考えてもらってもおおよそ構いません(無いとは言っていない¹²)．測度論の導入により，積分できる関数が大きく広がったのです．

以下，$|f|$ の積分を考えることができる関数 $f$ を可測関数，特に $\int |f| , dx < \infty$ となる関数を可積分関数と呼ぶことにします．

発展 ルベーグ積分は"横に切る"とよくいわれる

※ この節は飛ばしても問題ありません(重要だけど)

ルベーグ積分は，しばしば「横に切る」といわれることがあります．リーマン積分が縦に長方形分割するのに比較してのことでしょう．

確かに，ルベーグ積分は横に切る形で定義されるのですが，これは必ずしもルベーグ積分を上手く表しているとは思いません．例えば，初心者の方が以下のようなイメージを持たれることは，あまり意味がないと思います．

ここでは，"横に切る"，すなわちルベーグ積分の構成を，これまでの議論を踏まえて簡単に解説しておきます．

測度を用いたルベーグ積分の構成

以下のような関数 $f(x)$ を例に，ルベーグ積分の定義を考えていくことにします．

Step1 横に切る

図のように適当に横に切ります($n$ 個に切ったとします)．

Step2 切った各区間において，関数の逆像を考える

各区間 $[t_i, t_{i+1})$ において，$ \{ , x \mid t_i \le f(x) < t_{i+1} ,\}$ となる $x$ の集合を考えます(この集合を $A_i$ と書くことにします)．

Step3 A_i の長さを測る

これまで測度は「面積の重みづけ」だといってきましたが，これは簡単にイメージしやすくするための嘘です．ごめんなさい．
ルベーグ測度の場合，長さの重みづけといった方が正しいです(脚注7,8辺りも参照)．$x$ 軸上の「長さ」に重みをつけます．

$\mu$ をルベーグ測度とし，$\mu(A_i)$ で $A_i$ の(重み付き)長さを表すことにしましょう．

Step4 各区間で面積計算する

$t_i \times \mu(A_i) $ で，$A_i$ 上の $f$ の積分を近似します．

同様にして，各 $1 \le i \le n$ に対して積分を近似し，足し合わせたものがルベーグ積分の近似になります．

\int _a^b f(x) \, dx \; \approx \; \sum _{i=1}^n t_i \mu(A_i)

この近似において，$y$ 軸の分割を細かくしていくことで，ルベーグ積分を構成することができるのです¹³．

積分の概念を広げたことによるメリット

ここまで積分の概念を広げてきましたが，そもそもどうして積分の概念を広げる必要があるのか，数学的メリットについて記述していきます．

limと積分の交換が容易

積分の概念自体を広げてしまうことで，無駄な可積分性の議論を減らし，limと積分の交換を容易にしています．

これがメリットとしては非常に大きいです．数学では極限(limit)の議論は頻繁に出てくるため，両者の交換も頻繁に行うことになります．少し難しいですが，「お気持ち」だけ捉えるつもりで，そのような定理の内容を見ていきましょう．

単調収束定理(MCT)
$ \{f_n\}$ が非負可測関数列で，各点で単調増加に $f_n(x) \to f(x)$ となるとき，$$ \lim_{n\to \infty} \int f_n , dx ; = ; \int f , dx.$$

---

優収束定理/ルベーグの収束定理(DCT)
$\{f_n\}$ が可測関数列で，各点で $f_n(x) \to f(x)$ であり，さらにある可積分関数 $\varphi$ が存在して，任意の $n$ や $x$ に対し $|f_n(x)| \le \varphi (x)$ を満たすと仮定する．このとき，$$ \lim_{n\to \infty} \int f_n , dx ; = ; \int f , dx.$$

$ f = \lim_{n\to \infty} f_n $なので，これはlimと積分が交換できたことになります．

"重み"をいじることもできる

重みを定式化することで，重みを変えることもできます．

Dirac測度

$$f(0) = \int_{-\infty}^{\infty} f , d\delta_0.$$
但し，$f$は適当な関数，$\delta_0$はDirac測度，$\int \cdots , d\delta_0 $ で $\delta_0$ による積分を表す．

Dirac測度は，$x = 0$ の点だけに重みがあり，残りの部分の重みは $0$ である測度です．これを用いることで，ただの1つの値を積分の形に書くことが出来ました．

同じようにして， $n$ 個の値の和を取り出したり， $\sum_{n=0}^{\infty} f(n)$ を(適当な測度を使って)積分の形で表すこともできます．

確率測度

$$ \int_\Omega 1 , dP = 1.$$
但し，$P$ は確率測度，$\Omega$ は確率空間．

全体の重みの合計が $1$ となる測度のことです．これにより，連続的な確率が扱いやすくなり，また離散的な確率についても，(上のDirac測度の類似で離散化して，)高校で習った「同様に確からしい」という概念をちゃんと定式化することができます．

発展 L^pノルムと関数解析

※ この節は飛ばしても問題ありません(重要だけど)

情報系の方なら，行列の $L^p$ノルム等を考えたことがあるかもしれません．同じような原理で，関数にもノルムを定めることができ，関数解析の基礎となります．以下，関数解析における重要な言葉を記述しておきます．
測度論はそれ自身よりも，このように活用されて有用性を発揮します．

ルベーグ可測関数 $ f: \mathbb{R} \to \mathbb{C} $ に対し，$f$ の $L^p$ノルム$(1\le p < \infty)$を
$$ || f ||_p ; = ; \left( \int _{-\infty}^\infty |f(x)|^p , dx \right)^{ \frac{1}{p} } ,$$

$L^\infty$ノルムを
$$ ||f||_\infty ; = ; \inf _{a.e.} , \sup _{x} |f(x)| $$

で定めることにする¹⁴．
ここで，$||f||_p < \infty $ となるもの全体の集合 $L^p(\mathbb{R})$ を考えると，これは($a.e.$同一視の下で)ノルム空間(normed space)(ノルムが定義されたベクトル空間(vector space))となる．
特に，$p=2$ のときは，内積を
$$ (f, g) ; = ; \int _{-\infty}^\infty f(x) \overline{g(x)} , dx $$

と定めることで内積空間(inner product space)となる．
完備なノルム空間，内積空間をそれぞれバナッハ空間(Banach space)，ヒルベルト空間(Hilbert space)という($L^p(\mathbb{R})$ は完備である．これは測度を導入したからこその性質で，非常に重要である¹⁵)．

また，積分の概念を広げたのを用いて，今度は微分の概念を広げ，微分可能な関数の集合を考えることができる．
そのような空間をソボレフ空間(Sobolev space)という．

さらに，関数解析の基本的な定理を一つ紹介しておきます．

$$ C_C(\mathbb{R}) = \big\{f: \mathbb{R} \to \mathbb{C} \mid f ,\text{は連続}, \{, x \mid f(x) \neq 0 \} \text{は有界} \big\} $$

と定義する¹⁶と，以下の定理がいえる．

---

定理
任意の $f \in L^p(\mathbb{R}); (1 \le p < \infty)$ に対し，ある関数列 $ \{f_n\} \subset C_C(\mathbb{R}) $ が存在して，
$$ || f - f_n ||_p \longrightarrow 0 \quad( n \to \infty)$$
が成立する．

この定理はすなわち，変な関数を，連続関数という非常に性質の良い関数を用いて近似できることをいっています．関数解析の主たる目標の一つは，このような近似にあります．

測度論を本格的に学ぶためには

最後に，測度論を本格的に学ぶために必要な前提知識などを挙げておきます．

必要な前提知識

• 大学初級レベルの微積分

計算はもちろん，例えば「非負数列の無限和は和を取る順序によらない」等の事実は知っておいた方が良いでしょう．

• 可算無限と非可算無限の違い(脚注11なども参照)

これが分からないと「σ加法族」などの基本的な定義を理解したとはいえないでしょう．

• 位相空間論の初歩

「Borel加法族」を考える際に使用します．測度論を本格的にやろうと思わなければ，知らなくても良いでしょう．

下2つに関しては，本格的な「集合と位相」の本であれば両方載っているので，前提知識は実質2つかもしれません．

また，簡単な測度論の本なら，全て説明があるので前提知識はなくても良いでしょう．

参考になるページ

本来はちゃんとした本を紹介したほうが良いかもしれません．しかし，数学科向けの本と工学向けの本では違うだろうし，自分に合った本を探してもらう方が良いと思うので，そのような紹介はしません．代わりに，参考になりそうなウェブサイトを貼っておきます．

• よくわかる測度論とルベーグ積分(ベック日記)
• 測度論(Wikipedia)
• ルベーグ積分(Wikipedia)

余談 測度論は機械学習に必要か？

前提として，私は機械学習の数理的アプローチを専攻にしているわけではありません．なので，この質問に正しい回答はできません．
ただ，一つ言えることは，本気で測度論をやろうと思えば，それなりに時間がかかるということです．また，測度論はあくまで解析学の基礎であり，関数解析や確率論などに進まないとあまり意味がありません．そこまでちゃんと勉強しようと思うと，多くの時間を必要とするでしょう．

一方で，機械学習を数理的に研究しようと思うと，関数解析/確率論/情報幾何/代数幾何などが必要だといいます．自分にとってこれらが必要かどうかを見極めることが大事だと思います．

おわりに

SNS上で，「機械学習に測度論は必要か」などの議論をよく見かけるのですが，初心者にもわかりやすい測度論の記事が少ないなと思ったので，書いてみました．

いくつか難しい単語も出てきましたが，なんとなく測度論のイメージを掴めたら幸いです．ありがとうございました．

1. 他の数学科の方々に怒られそうだ…….なお，よく測度は「長さを測る」とも説明されますが，距離位相と違った測度を考えることだってできるので，ここでは「重みづけ」という表現を使うことにします． ↩

2. すなわち，集合 $ \{, x \mid 0 \le x \le 1 , \} $ 上． ↩

3. 分割が実際には等間隔でなくても良いからです．リーマン積分(Wikipedia)等を参照． ↩

4. ディリクレの関数という．記法は定義関数による． ↩

5. 2つの任意の実数 $a < b $ に対して，その間に必ず有理数や無理数があることが知られています．すなわち，$ a < c < b $ をみたす有理数 $c$ ，無理数 $c$ があることが知られています．ちなみに，「稠密」という言葉の厳密な定義には「位相空間論」の概念を使用します． ↩

6. 面積に限らず，$n$ 次元体積の「重み/尺度」を議論することもできるし，もっと一般化することもできます．また，今回の文脈では，本当は「長さの重みづけ」と言った方が正しいです．重みをつけるのは $[0,1]$ 区間や実数上だからです． ↩

7. もう少しだけ踏み込むと，集合 $X$ 上の 測度 $\mu$ とは， $X$ の「性質の良い」部分集合を投げると，$0$ 以上 $\infty$ 以下の値を返す集合関数です(未満でなく以下であることに注意)．「性質の良い」集合を可測集合(measurable set)，可測集合の集まりをσ加法族(σ-field)といいます．本文中はイメージとして，「長さや面積の重みづけ」といいましたが，集合の「長さや面積」というものがあってそこに重みをつけるというよりも，そもそも「集合の長さや面積自体を測る尺度」すなわち集合関数として測度は存在するといった方が正確かもしれません． ↩

8. 測度論の画期的なところは，議論できるクラスを有限から可算無限(可算集合, cf.注11)へと拡張したことにあります．これにより，sequence がかなり扱いやすくなり，その例が単調収束定理やルベーグの収束定理です． ↩

9. 広義積分は除きます．例えば，$ \int_{-\infty}^\infty $ となる積分のことです． ↩

10. 有理数は可算集合，無理数は非可算集合．可算集合とは，順番を適当に並び替えることで正の整数で順番付けできる集合のことを言います．言い換えれば，正の整数との全単射が存在する集合を指します．詳しくは濃度(数学)(Wikipedia)などを参照． ↩

11. 1点の「面積の重み」が0で，測度は可算無限に広げたものなので，可算集合も重み0となります(cf.注9,11)． ↩

12. ルベーグ積分不可能な関数は次の2種類． 1. $\int_a^b |f| , dx = \infty $ となるもの， 2. ルベーグ可測でないもの．2の構成には選択公理を考える必要があり，この公理が正しいかどうか，現実世界ではわからない(数学上は，多くの場合で認める重要な公理である)． ↩

13. 同様にして，$1_\mathbb{Q}$ に関して，$\mu([0,1] \cap \mathbb{Q}) = 0, ; \mu([0,1] \cap \mathbb{Q}^c) = 1$ なので，積分が $0$ になります． ↩

14. $L^\infty$ノルムは，測度を $\mu$ として $||f||_\infty = \inf , \{ , a \mid \mu(\{ x\mid | f(x) | > a \} ) = 0 \} $ と定義することが多いです． ↩

15. リーマン積分でも，似たようにして $L^p$ ノルム $(1 \le p < \infty)$ を導入し，$||f||_p < \infty$ となるものの集まりを考えることはできますが，これは完備にならず，性質が良くないです．(ルベーグ積分が sequence に強いことがこのことからも分かります) ↩

16. 記法について，$C(X)$ で， $X$ 上連続な複素数値(or実数値)関数の集合を表し，$C_C(X)$ で，$\text{supp}, f = \overline{ \{ , x \mid f(x) \neq 0 \} }$ がコンパクトな連続関数の集合を表します(上付き線やコンパクトは位相空間の概念)． ↩