人生プラスマイナスゼロの法則は嘘なのか!? ～arcsin則の確率論的理論とシミュレーション～

確率論には，逆正弦法則 (arc-sine law, arcsin則) という，おおよそ一般的な感覚に反する定理があります．この定理を身近なテーマに当てはめて紹介していきたいと思います。

注意・おことわり
今回は数学的な話を面白く，そしてより身近に感じてもらうために，少々極端なモデル化を行っているかもしれません．気になる方は適宜「コイントスのギャンブルモデル」など，より確率論が適用できるモデルに置き換えて考えてください．
意見があればコメント欄にお願いします．

考えてみてほしい

自分がどのくらいの時間「幸運」かを考えましょう．自分の「運の良さ」は時々刻々と変化し，偶然に支配されているものとします．

さて，上のグラフにおいて，「幸運な時間」を上半分にいる時間，「不運な時間」を下半分にいる時間として，自分が人生のうちどのくらいの時間が幸運/不運なのかを考えてみたいと思います．

ここで，「人生プラスマイナスゼロの法則」とも呼ばれる，一般に受け入れられている通説を紹介します¹．

人生プラスマイナスゼロの法則 (人生バランスの法則)
人生には幸せなことと不幸なことが同じくらい起こる．

この法則にしたがうと，
「運が良い時間と悪い時間は半々くらいになるだろう」
と推測がつきます．
あるいは，確率的含みを持たせて，以下のような確率密度関数 $f(x)$ になるのではないかと想像されます．

(累積)分布関数 $F(x) = \int_{-\infty}^x f(y) , dy$ も書いてみるとこんな感じでしょうか．

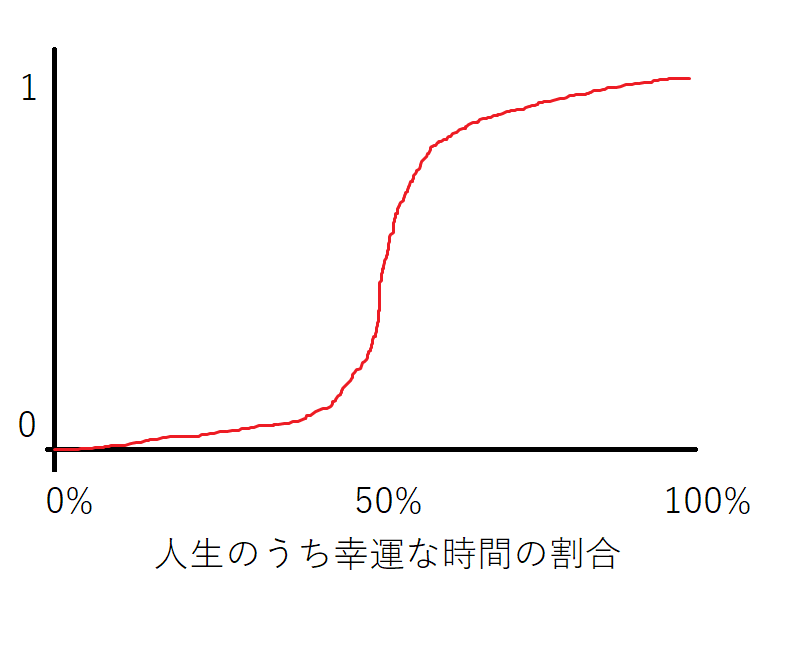
しかし，以下に示す通り，この予想は見事に裏切られることになります．

なお，ここでは「幸運/不運な時間」を考えていますが，例えば**「幸福な時間/不幸な時間」**などと言い換えても良いでしょう．

他にも，**「コイントスで表が出たら $+1$ 点，そうでなかったら $-1$ 点を加算するギャンブルゲーム」**と思ってもいいです．

以上3つの問題について，モデルを仮定し，確率論的に考えてみましょう．

考える数学的モデル ～ブラウン運動～

ブラウン運動を考えます．

定義：ブラウン運動 (Brownian motion)²

ブラウン運動 $B(t)$ とは，以下をみたす確率過程のことである．( $t$ は時間パラメータ)

• $B(0) = 0.$
• $B(t)$ は連続．
• $B(t) - B(s) \sim N(0, t-s) ;; s < t.$
• $B(t_1) - B(t_2),, B(t_2) - B(t_3) , \dots , B(t_{n-1}) - B(t_n) ;; t_1 < \dots < t_n$ は独立(独立増分性)．

但し，$N(0, t-s)$ は平均 $0$，分散 $t-s$ の正規分布を表す．

今回は，上で挙げた「幸運/不運」，あるいは「幸福/不幸」の推移をブラウン運動と思うことにしましょう．

モデル化に関する補足 (スキップ可)

この先，運や幸せ度合いの指標を「ブラウン運動」と思って議論していきますが，そもそもブラウン運動とみなすのはいかがなものかと思うのが自然だと思います．本格的な議論の前にいくつか補足しておきます．

• 実際の「幸運/不運」「幸福/不幸」かどうかは偶然ではない，人の意思によるものも大きいのではないか．(特に後者)
  → 確かにその通りです．今回ブラウン運動を考えるのは，現実世界における指標というよりも，むしろ**人の意思等が介入しない，100%偶然が支配する「完全平等な世界」**と思ってもらった方がいいかもしれません．幸福かどうかも，偶然が支配する外的要因のみに依存します(実際，外的要因ナシで自分の幸福度が変わることはないでしょう)．あるいは無難に「コイントスゲーム」と思ってください．

• 実際の「幸運/不運」「幸福/不幸」の推移は，連続なものではなく，途中にジャンプがあるモデルを考えた方が適切ではないか．
  → その通りです．しかし，その場合でも，ブラウン運動の代わりに適切な条件を課した レヴィ過程 (Lévy process) を考えることで，以下と同様の結論を得ることができます³．しかし，レヴィ過程は一般的過ぎて，議論と実装が複雑になるので，今回はブラウン運動で考えます．

上図はレヴィ過程の例．実際はこれに微小なジャンプを可算個加えたような，もっと一般的なモデルまで含意する．[Kyprianou] より引用．

• 「幸運/不運」「幸福/不幸」はまだしも，「コイントスゲーム」はブラウン運動ではないのではないか．
  → 単純ランダムウォークは試行回数を増やすとブラウン運動に近似できることが知られている⁴ので，基本的に問題ありません．単純ランダムウォークから試行回数を増やすことで，直接arcsin則を証明することもできます(というか多分こっちの方が先です)．[Erdös, Kac]

ブラウン運動のシミュレーション

中心的議論に入る前に，まずはブラウン運動をシミュレーションしてみましょう．Python を使えば以下のように簡単に書けます．

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
matplotlib.rcParams['font.family'] = 'IPAexGothic'
sns.set(font='IPAexGothic')
# 以上は今後省略する

# 0 <= t <= 1 をstep等分して，ブラウン運動を近似することにする
step = 1000
diffs = np.random.randn(step+1).astype(np.float32) * np.sqrt(1 / step)
diffs[0] = 0.
x = np.linspace(0, 1, step+1)
bm = np.cumsum(diffs)

# 以下描画
plt.plot(x, bm)
plt.xlabel("時間 t")
plt.ylabel("値 B(t)")
plt.title("ブラウン運動の例")
plt.show()

もちろんブラウン運動はランダムなものなので，何回もやると異なるサンプルパスが得られます．

step = 1000
num = 5

diffs = np.random.randn(num, step+1).astype(np.float32) * np.sqrt(1 / step)
diffs[:, 0] = 0.
x = np.linspace(0, 1, step+1)
bms = np.cumsum(diffs, axis=1)
for bm in bms:
    plt.plot(x, bm)
# 以下略

本題に戻ります．

問題の定式化

今回考える問題は，"人生のうち「幸運/不運」(あるいは「幸福/不幸」)の時間はどのくらいあるか"でした．これは以下のように定式化されます．

$$ L(t) := [0,t] \text{における幸運な時間} = \int_0^t 1_{\{B(s) > 0\}} , ds.$$
但し，$1_{\{ . \}}$ は定義関数．

このとき，$L(t)$ の分布がどうなるかが今回のテーマです．

レヴィの逆正弦法則 (Arc-sine law of Lévy)

さて，いきなり結論を述べましょう．今回の問題は，逆正弦法則 (arcsin則) として知られています．

レヴィの逆正弦法則 (Arc-sine law of Lévy) [Lévy]

$L(t) = \int_0^t 1_{\{B(s) > 0\}} , ds$ の(累積)分布関数は以下のようになる．

$$ P(L(t) \le x), = , \frac{2}{\pi}\arcsin \sqrt{\frac{x}{t}}, ,,, 0 \le x \le t.$$

但し，$y = \arcsin x$ は $y = \sin x$ の逆関数である．

(累積)分布関数から，逆関数の微分により確率密度関数 $f(x)$ を求めると以下のようになります．

$$f(x), = , \frac{1}{\pi\sqrt{x(t-x)}}.$$

上で，今回は $t = 1$ と思うことにしましょう．
これを図示してみましょう．以下を見てください．

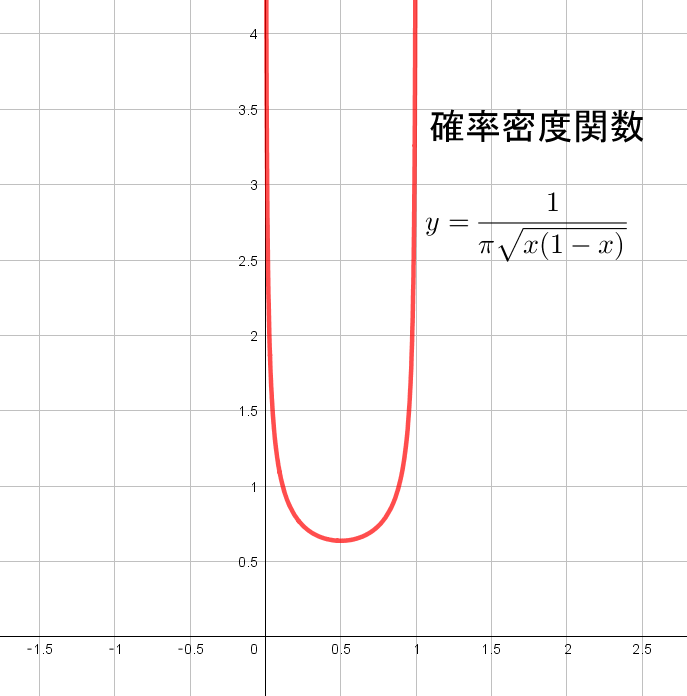
えええ，確率密度関数をみれば分かると思いますが，冒頭の予想と全然違います． 確率密度関数は山型になると思ったのに，むしろ谷型で驚きです．まだにわかに信じられませんが，とりあえずシミュレーションしてみましょう．

シミュレーション

各ブラウン運動のステップ数を 1000 とし，10000 個のサンプルパスを生成して理論値と照らし合わせてみましょう．

step = 1000
num = 10000

diffs = np.random.randn(num, step+1).astype(np.float32) * np.sqrt(1 / step)
diffs[:, 0] = 0.
bms = np.cumsum(diffs, axis=1)
# 正の滞在時間を各ステップが正かで近似
cal_positive = np.mean(bms[:, 1:] > 0, axis=1)
# 理論値
x = np.linspace(0.005, 0.995, 990+1)
thm_positive = 1 / np.pi * 1 / np.sqrt(x * (1 - x))
xd = np.linspace(0, 1, 1000+1)
thm_dist = (2 / np.pi) * np.arcsin(np.sqrt(xd))

# 以下描画
plt.figure(figsize=(15, 6))
plt.subplot(1, 2, 1)
plt.hist(cal_positive, bins=50, density=True, label="シミュレーション")
plt.plot(x, thm_positive, linewidth=3, color='r', label="理論値")
plt.xlabel("B(t) (0<=t<=1)の正の滞在時間")
plt.xticks(np.linspace(0, 1, 10+1))
plt.yticks(np.linspace(0, 5, 10+1))
plt.title("L(1)の確率密度関数")
plt.legend()
plt.subplot(1, 2, 2)
plt.hist(cal_positive, bins=50, density=True, cumulative=True, label="シミュレーション")
plt.plot(xd, thm_dist, linewidth=3, color='r', label="理論値")
plt.xlabel("B(t) (0<=t<=1)の正の滞在時間")
plt.xticks(np.linspace(0, 1, 10+1))
plt.yticks(np.linspace(0, 1, 10+1))
plt.title("L(1)の分布関数")
plt.legend()
plt.show()

理論値と同じような結果になりました．

これから何が分かるのか

今回，人の「幸運/不運」を考えたモデルは，現実世界というよりも「完全に平等な世界」であるし，そうであればみんな同じくらい幸せを感じると思うのは自然でしょう．でも実際はそうではありません．完全平等な世界においても，幸運(幸福)を感じる時間が長い人と，不運(不幸)を感じるのが長い人とが完全に両極端に分かれるのです．
「自分の人生は不幸ばかり感じている」という思っている方も，確率論的に少数派ではないのです．

今回のモデル化は少し極端だったかもしれませんが，平等とはそういうものであり得るということは心に留めておくと良いかもしれません.

別の視点から「幸運度」を測る

arcsin則を紹介する，という観点からは，この記事はここで終わっても良いのですが，上だけ読んで「人生プラスマイナスゼロの法則は嘘である」と結論付けられるのもあれなので，「幸運度」あるいは「幸福度」を別の評価指標で測ってみましょう．

積分で定量的に評価

上では「幸運/不運な時間」のように，時間のみで評価しました．しかし，実際は幸運の程度もちゃんと考慮した方が良いでしょう．

次は，以下の積分値で「幸運度/不運度」を測ってみることにします．

$$I(t) , := , \int_0^t B(s) , ds.$$

このとき，以下の定理が知られています．

定理
ブラウン運動の積分 $I(t) = \int_0^t B(s) , ds$ について，
$$ I(t) \sim N \big{(}0, \frac{1}{3}t^3 \big{)}$$
が成立する．

考察を挟まずシミュレーションしてみましょう．再び $t=1$ とします．

step = 1000
num = 10000

diffs = np.random.randn(num, step+1).astype(np.float32) * np.sqrt(1 / step)
diffs[:, 0] = 0.
bms = np.cumsum(diffs, axis=1)
cal_inte = np.mean(bms[:, 1:], axis=1)
x = np.linspace(-3, 3, 1000+1)
thm_inte = 1 / (np.sqrt(2 * np.pi * (1 / 3))) * np.exp(- x**2  / (2 * 1/3))
thm_cum = np.cumsum(thm_inte) / len(x) * 6


plt.figure(figsize=(15, 6))
plt.subplot(1, 2, 1)
plt.hist(cal_inte, bins=50, density=True, range=(-3, 3), label="シミュレーション")
plt.plot(x, thm_inte, linewidth=3, color='r', label="理論値")
plt.xlabel("B(t) (0<=t<=1)の積分値")
plt.title("I (1)の確率密度関数")
plt.legend()
plt.subplot(1, 2, 2)
plt.hist(cal_inte, bins=50, density=True, cumulative=True, range=(-3, 3), label="シミュレーション")
plt.plot(x, thm_cum, linewidth=3, color='r', label="理論値")
plt.xlabel("B(t) (0<=t<=1)の積分値")
plt.title("I (1)の分布関数")
plt.legend()
plt.show()

こちらはちゃんと山型の密度関数を持つようで，偶然が支配する完全平等な世界における定量的な「幸運度/幸福度」は，みんなおおよそプラスマイナスゼロである，という結果になりました．

話がややこしくなってきました．幸運/幸福な時間は人によって大きく偏りが出るのに，度合いはみんな大体同じという，一見矛盾した2つの結論が得られたわけです．
そこで，同時確率密度関数を描いてみることにします．
(同時分布の理論はよく分からないのですが，詳しい方がいたら教えてください．)

同時密度関数の図示

step = 1000
num = 300000   # 大分増やした

diffs = np.random.randn(num, step+1).astype(np.float32) * np.sqrt(1 / step)
diffs[:, 0] = 0.
bms = np.cumsum(diffs, axis=1)
cal_inte = np.mean(bms[:, 1:], axis=1)
cal_positive = np.mean(bms[:, 1:] > 0, axis=1)

# 以下描画
sns.jointplot(x=cal_positive, y=cal_inte, xlim=(0, 1), ylim=(-2, 2), color="g", kind='hex').set_axis_labels('正の滞在時間 L(1)', '積分 I(1)')
plt.show()

同時分布の解釈

この解釈は難しいところでしょうが，簡単にまとめると，

人生の「幸運度/幸福度」を定量的に評価すれば，大体みんな同じくらいになるという点で「人生プラスマイナスゼロの法則」は正しい．しかし，それは「幸運/幸福を感じている時間」がそうでない時間と同じになるというわけではなく，どのくらい長い時間幸せを感じているのかは人によって大きく異なるし，偏る．

くらいでしょうか．
かなり大雑把なことを言ったような気がしますが，この辺の解釈は難しいところだと思うので，正確な解釈は読者の演習問題としましょう．

まとめ

今回は，arcsin則の理論とそれに関連したテーマを，面白おかしく取り上げました．「人生プラスマイナスゼロの法則」に対する結論は少々あいまいなままですが，「平等」という言葉に対する考え方が変わったかもしれません．

今回のコードは ココ(Google Colaboratory) に置いておきますので，気になった方は追試してみてください．

みなさんの今日という日が幸せでありますように．

参考

1. A. E. Kyprianou, Fluctuations of Lévy Processes with Applications, Springer, 2006.
2. H. Kuo, Introduction to Stochastic Integration, Springer, 2006.
3. L. Breiman, Probability, Society for Industrial and Applied Mathematics, 1992.
4. P. Erdös, M. Kac, On The Number of Positive Sums of Independent Random Variables, Bulletin of the American Mathematical Society, 1947.
5. P. Lévy, Sur certains processus stochastiques homogines, Compositio Math 7 1939, 283–339.
6. R. K. Getoor and M. J., Sharpe On the Arc-Sine Laws for Lévy Processes, Journal of Applied Probability Vol. 31, No. 1, Mar. 1994, 76-89.

1. ここでは，通説の解釈の是非は問題にしないことにします(笑) ↩

2. ウィーナー過程 (Wiener Process) ともいう． ↩

3. 例えば，$P(X(t) > 0) = 1/2, ;; t \ge 0$ とすると，$\lim_{t \to \infty} \frac{1}{t} \int_0^t X(s) , ds$ (分布収束) の意味で成立する．[Getoor, Sharpe] ↩

4. 単純ランダムウォークはブラウン運動に「ある意味」分布収束する． ↩