確率有限要素法なる分野に興味をもったので、学んだことをまとめてみたいと思います。
はじめに
実世界における構造物の振る舞いを考えると、様々な不確定な因子があることに気づきます。
これらの不確定性は大きく分けて次の2つに分類されます。
- 入力の不確実性
- 構造物そのものの不確定性
地震や流体による加振入力のような非再現的な入力が、1つ目の「入力の不確実性」に分類されます。入力の不確実性においては、その想定されうる上限入力値に対する応答を求めるなど、比較的容易に対応することができます。
確率有限要素法で主に取り扱われるのは、2つ目の「構造物そのものの不確実性」です。
実在の構造物は、公差の範囲で図面形状に対して不確実性を含んでいます。また、理想的な部品においては、全体にわたって材料特性が均一なのに対し、実世界の部品における材料特性は不均一な分布をもっています。確率有限要素法においては、こうした「形状」「材料特性」といった"モデルのゆらぎ”に対する"応答のゆらぎ"を数理的に関連付け、数値的に求めることを試みています。
今回は手計算レベルの二自由度系を題材に、摂動法に基づく確率有限要素法の計算を追ってみます。
摂動法に基づく確率有限要素法の基本アイデア
有限要素法について
簡単のため、今回は線形弾性体の微小変形静解析(以下、線形解析)に絞る。
有限要素法による線形解析は、一般に下記のような線形方程式に帰着する。
[K]\{u\}=\{f\}\tag{1}
ただし、$[K]$は剛性マトリクス、${u}$節点変位ベクトル、$f$は外力ベクトルである。冒頭で述べた、「入力の不確実性」は外力ベクトルの不確実性としてモデル化されるため、$[K]$が定まりさえすれば上式を${u}$について解くことでその影響を見積もることができる。
一方で、二つ目の「構造物そのものの不確実性」方程式そのものが定まらないため、扱いには工夫を要する。
2自由度系の静解析
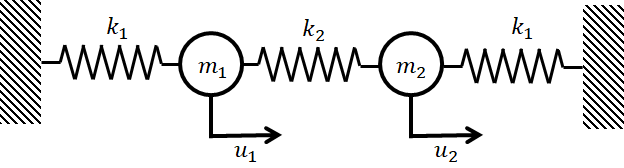
上図のような2自由度のバネマス系について考える。
この系におけるつり合い方程式は下記のように表せる。
\begin{bmatrix}
k_1+k_2 & -k_2 \\
-k_2 & k_1+k_2
\end{bmatrix}
\left\{
\begin{matrix}
u_1 \\
u_2
\end{matrix}
\right\}=
\left\{
\begin{matrix}
f_1 \\
f_2
\end{matrix}
\right\}\tag{2}
変位について解くと、下記のようになる。
\left\{
\begin{matrix}
u_1 \\
u_2
\end{matrix}
\right\}=\frac{1}{k_1\left(k_1+2k_2\right)}
\left\{
\begin{matrix}
f_1(k_1+k_2) + f_2k_1\\
f_1k_1 + f_2(k_1+k_2)
\end{matrix}
\right\}\tag{3}
確率変数$\{\varepsilon_1, \varepsilon_2\}$と応答$\{u_1, u_2\}$を紐づけるもっとも単純なアイデアとしては、変位の確率密度関数$f_U(u_1, u_2)$を、不確実性を含むパラメータ$\{\varepsilon_1,\varepsilon_2\}^{T}$の確率密度関数$f_{\varepsilon}(\varepsilon_1, \varepsilon_2)$を用い表すことである。
これらの二つの確率密度関数は下記の式で関係づけられる。
f_U(u_1, u_2) = \frac{f_{\varepsilon}(\varepsilon_1, \varepsilon_2)}{\left|J\left(\frac{u_1, u_2}{\varepsilon_1, \varepsilon_2}\right)\right|}
ただし、$\left|J\left(\frac{u_1, u_2}{\varepsilon_1, \varepsilon_2}\right)\right|$はヤコビアンの絶対値を表す。式(3)のように確率変数$\{\varepsilon_1, \varepsilon_2\}$を用いて応答$\{u_1, u_2\}$を陽に表すことができる場合はこの取り扱いで問題ない。
しかし、実問題においてこれらを構築することは困難であり、$\left|J\left(\frac{u_1, u_2}{\varepsilon_1, \varepsilon_2}\right)\right|$を計算するのに非常に多くの時間を要してしまうことが想像できる。
そこで別の取り扱いを考える。
摂動法に基づく変動率の計算
下記のように、$\{\varepsilon_1, \varepsilon_2\}^{T} = \{0, 0\}^{T}$のまわりで剛性マトリクスをTaylor展開し、1次の項までで近似する。
\begin{align}
[K]
&= [\bar{K}] + [K_{,i}]\varepsilon_i + \frac{1}{2}[K_{,ij}]\varepsilon_i\varepsilon_j+...\\
&\approx [\bar{K}] + [K_{,i}]\varepsilon_i\\
\end{align}
ただし、$[\bar{K}]$は$\{\varepsilon_1, \varepsilon_2\}^{T} = \{0, 0\}^{T}$における剛性マトリクス(すなわち期待剛性)、添え字の$\square_{,i}$および$\square_{,ij}$はそれぞれ$\frac{\partial \square}{\partial \varepsilon_i}$および$\frac{\partial^2 \square}{\partial \varepsilon_i\varepsilon_j}$のような確率変数での偏微分を$\{\varepsilon_1, \varepsilon_2\}^{T} = \{0, 0\}^{T}$で評価した値を表す。また、アインシュタインの縮約規約で表現しているため、項の中で2つ以上現れる添え字については、その総和を取る。
応答についても、同様に$\{\varepsilon_1, \varepsilon_2\}^{T} = \{0, 0\}^{T}$のまわりでTaylor展開する。
\begin{align}
\{u\} &= \{\bar{u}\} + \{u_{,i}\}\varepsilon_i + \frac{1}{2}\{u_{,ij}\}\varepsilon_i\varepsilon_j+...
\end{align}
$\{u_{,i}\}$, $\{u_{,ij}\}$のような微分項を、その階数$n$に応じて$n$次変動率と呼ぶ。
これらの変動率を求めることで、確率変数$\varepsilon$の変動による応答$u$の変動を近似的に求めることができる。
また、$f_{\varepsilon}(\varepsilon_1, \varepsilon_2)$に乗じて積分することで期待値や分散といった情報も算出できる。
級数展開された2つの式を式(1)に代入すると下記のようになる。
\left([\bar{K}] + [K_{,i}]\varepsilon_i\right)\left(\{\bar{u}\} + \{u_{,i}\}\varepsilon_i + \frac{1}{2}\{u_{,ij}\}\varepsilon_i\varepsilon_j+...\right)=\{f\}\\
\left([\bar{K}]\{\bar{u}\} - \{f\}\right)
+ \left([K_{,i}]\{\bar{u}\} + [\bar{K}]\{u_{,i}\}\right)\varepsilon_i
+ \left([K_{,i}]\{u_{,j}\} + [K_{,j}]\{u_{,i}\} + \frac{1}{2}[\bar{K}]\{u_{,ij}\}\right)\varepsilon_i\varepsilon_j + ... = \{0\}
$\varepsilon$の次数毎に整理し、左右で等値すると下記のように変動率を求めることができる。
\begin{align}
0次:& \{\bar{u}\}=[\bar{K}^{-1}] \{f\}&\\
1次:& \{u_{,i}\} = - [\bar{K}^{-1}][K_{,i}]\{\bar{u}\}&\\
2次:& \{u_{,ij}\}= -[\bar{K}^{-1}]\left([K_{,i}]\{u_{,j}\} + [K_{,j}]\{u_{,i}\}\right)&\\
\end{align}
ただし、$\{u_{ij}\}=\{u_{ji}\}$であることを用いている。
上式から、低次の変動率から順に求めていくことで変動率を順次決定することができる。
逆行列は$[\bar{K}^{-1}]$のみ表れるため、一度求めた値を記憶することで高速に計算することができる。
具体例
先ほど取り上げた2自由度系を用いて変動率を求めてみる。ここではバネ定数$k_1$および$k_2$が、確率変数$\varepsilon_1$および$\varepsilon_2$に従って下記のように変動すると仮定する。
k_1 = \bar{k}_1(1+\varepsilon_1)\\
k_2 = \bar{k}_2(1+\varepsilon_2)
すると剛性マトリクス$[K]$の導関数や逆行列は、次のように計算される。
\begin{align}
[K^{-1}]&=\frac{1}{k_1\left(k_1+2k_2\right)}
\left[
\begin{matrix}
k_1+k_2 & k_2\\
k_2 & k_1+k_2
\end{matrix}
\right]\\
[K_{,1}]&=
\left[
\begin{matrix}
\bar{k}_1 & 0\\
0 & \bar{k}_1
\end{matrix}
\right]\\
[K_{,2}]&=
\left[
\begin{matrix}
\bar{k}_2 & -\bar{k}_2\\
-\bar{k}_2 & \bar{k}_2
\end{matrix}
\right]
\end{align}
各値を下表のように設定した場合の数値計算例を示す。
今回は2次までの変動率を用いて、$\{k_1, k_2\}$の変動に対する$\{u\}$の変化の様子を式(3)と比較する。
| 変数名 | 値 |
|---|---|
| $\bar{k}_1$ | 3.0 |
| $\bar{k}_2$ | 2.0 |
| $\bar{f}_1$ | 1.0 |
| $\bar{f}_2$ | -2.0 |
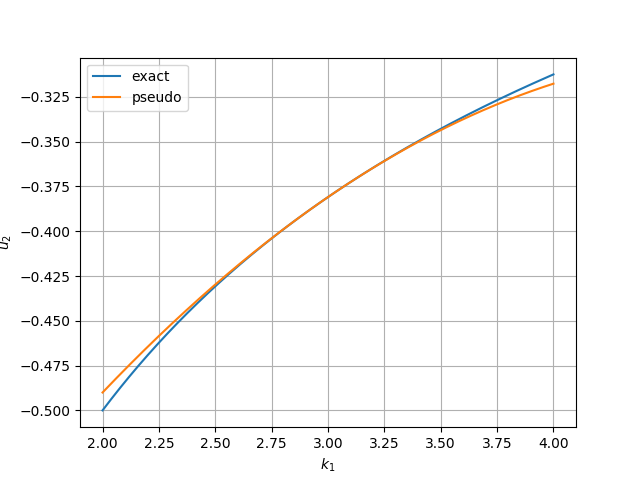
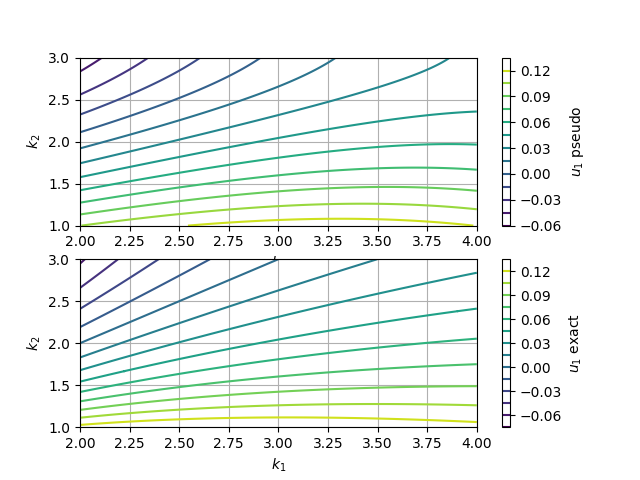
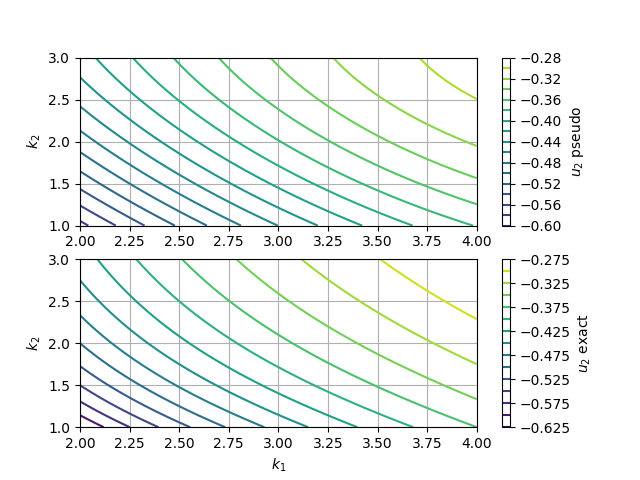
$\varepsilon_1$と$\varepsilon_2$の変動に対する$u_1$および$u_2$の変化の様子を下記に示す。
$k_2=2.0$に固定したとき、$\varepsilon_1$の変動に対する$u_1$および$u_2$の変化の様子を下記に示す。
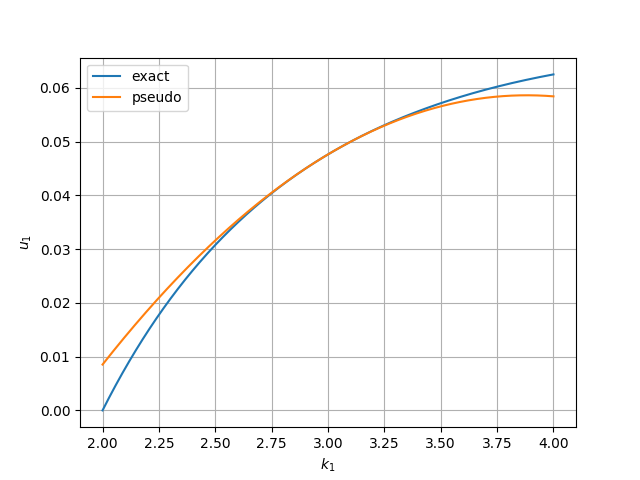
基本的にはTaylor展開なので、いずれのグラフを見ても展開の中心$\{k_1, k_2\}^{T} = \{3.0, 2.0\}$から離れるほど厳密な値との誤差が大きくなることが分かる。
ちなみに今回のケースでいうと、$[K_{,ij}]$は厳密に零行列になるため、計算される変動率は式(3)をTaylor展開したときの各項と厳密に一致する(はず)。
所感
不確実性を数理的に表現する方法および、剛性マトリクスの導関数の数値的な取り扱いがかなり難しいと感じた。特に商用ソフトウェアで$[K_{,i}]$を求めるのには工夫を要しそう。(数値微分が一番手っ取り早い?)
そのあたりについても今後調べてまとめていけたらなと思います。
参考
下記の記事と書籍の導入部分を参考にしました。
いずれも中桐滋先生の文献になります。
https://www.jstage.jst.go.jp/article/bjsiam/2/2/2_KJ00005767624/_pdf
Amazon: 確率有限要素法