More than 5 years have passed since last update.

スパースモデリング (3) MATLABで簡単スパースモデリング

Posted at 2017-10-28

カーブフィッティング

手軽にスパースモデリングを体験できる題材として，今回はカーブフィッティングを取り上げます．書籍「スパースモデリング」に掲載されている例題を詳しく解説します．

多項式補間の基本

カーブフィッティングで使われる最も単純なテクニックは多項式補間です．点と点の間を結ぶ曲線を求めるときに使います．

多項式補間では以下の性質が重要です．
2点が与えられれば，それらの点を通る直線（1次式）がただ一つ決まる．

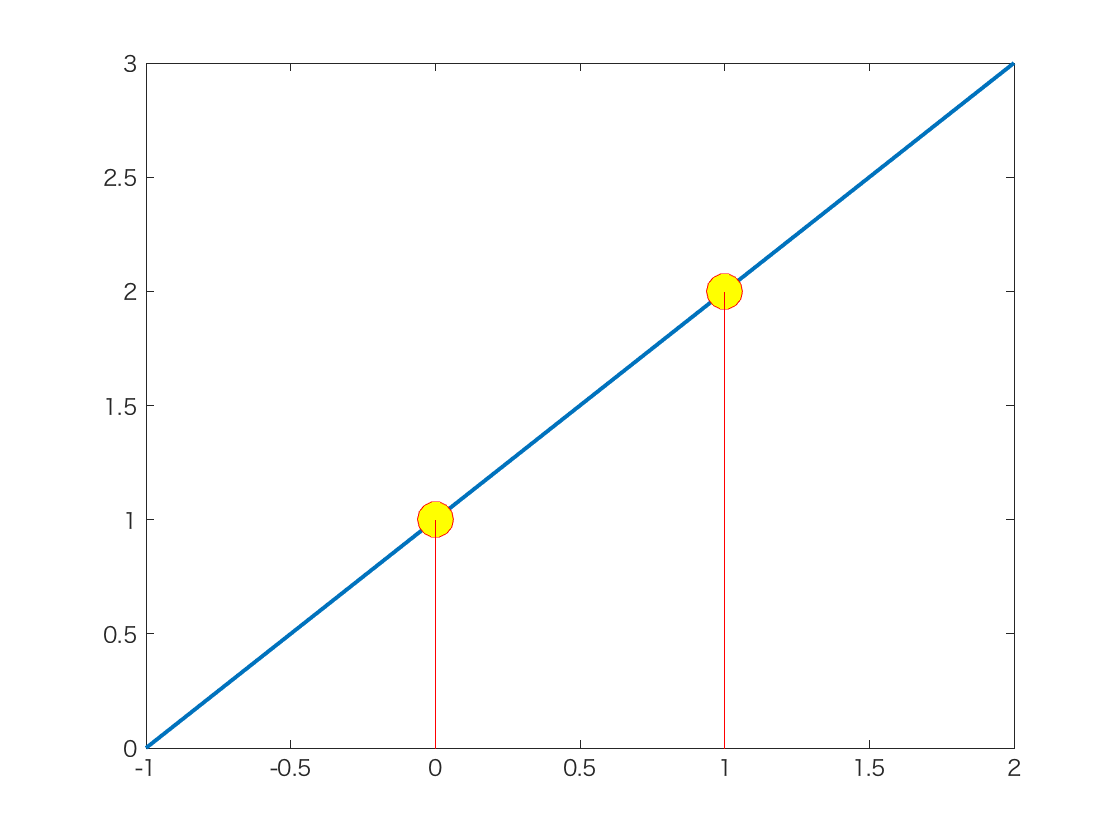
3点が与えられれば，それらの点を通る曲線（2次曲線）がただ一つ決まる．

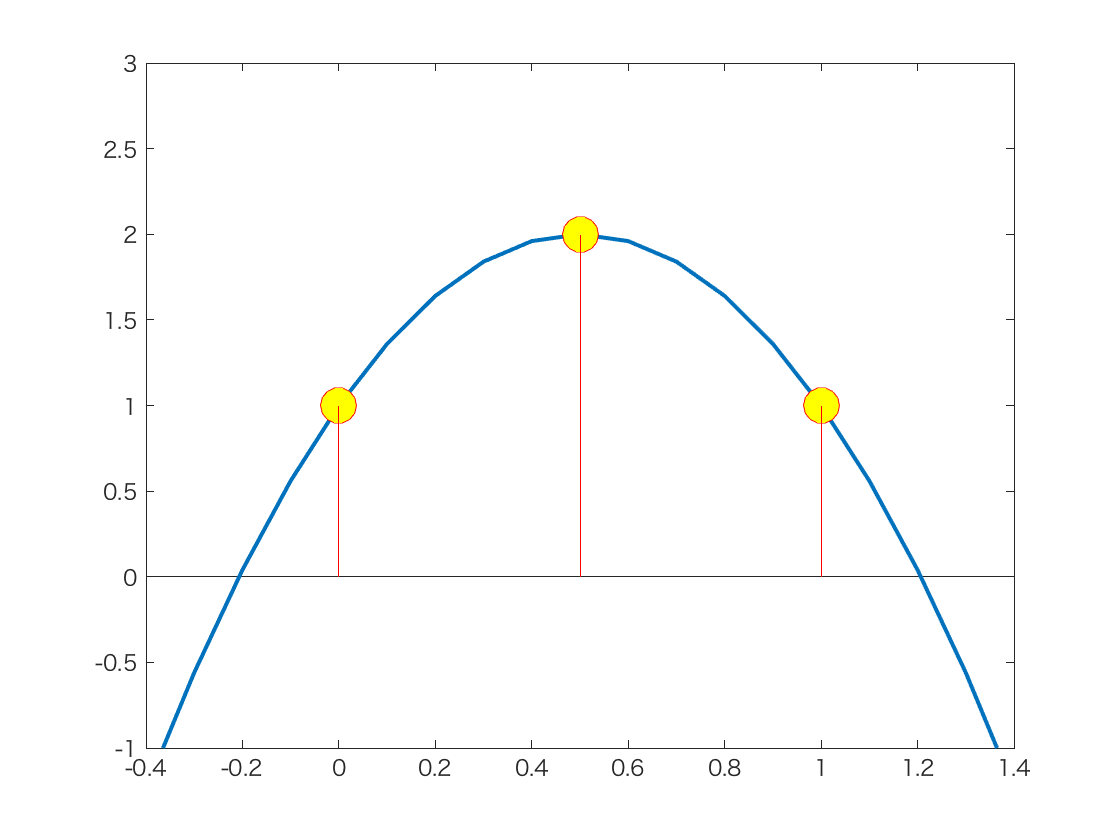
4点が与えられれば，それらの点を通る曲線（3次曲線）がただ一つ決まる．

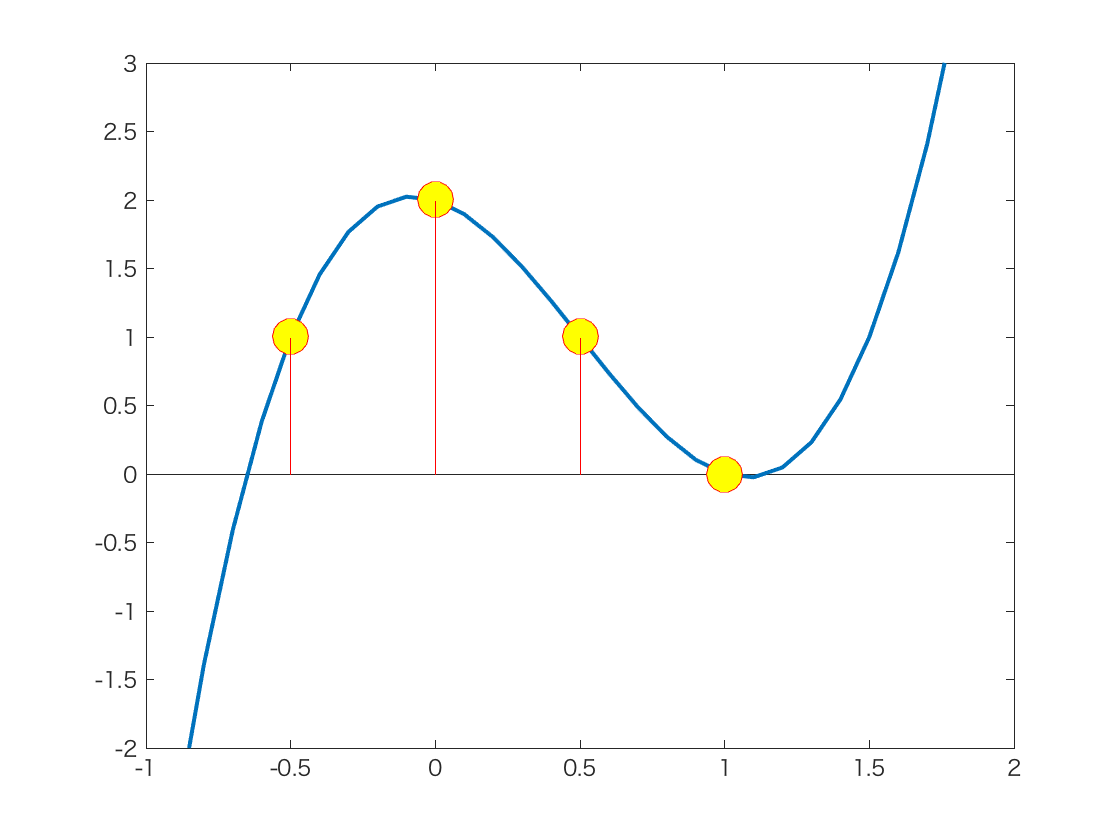
以上から，次の一般化が可能です．

N個の点が与えられれば，それらの点を通る曲線（N-1次曲線）がただ一つ決まる．

ここで，N-1次曲線というのは，N-1次の多項式で表される曲線のことです．

**問題：**80次曲線（80次の多項式で表される曲線）を決めるのに，何個の点が必要でしょうか？

上の原則から言えば，81個の点が必要ですよね．これをたった11点から求められますよ，というのがスパースモデリングです．ビッグデータならぬ，スモールデータ（足りないデータ）から予測しようというわけです．

スパースモデリングの問題

次の多項式
$$
y(t) = -t^{80}+t
$$
を考えます．この多項式に
$$
t = 0,~ 0.1,~ 0.2,\ldots,~ 0.9,~ 1
$$
の11点を代入して11組のデータを求めます．これは，以下のような値になります．

0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	0

$t$の値が1未満のとき，$t^{80}$は極めて小さい値になりますので， $-t^{80}+t\approx t$となり，表のような結果になります．

図示すると，以下のようなデータとなります．

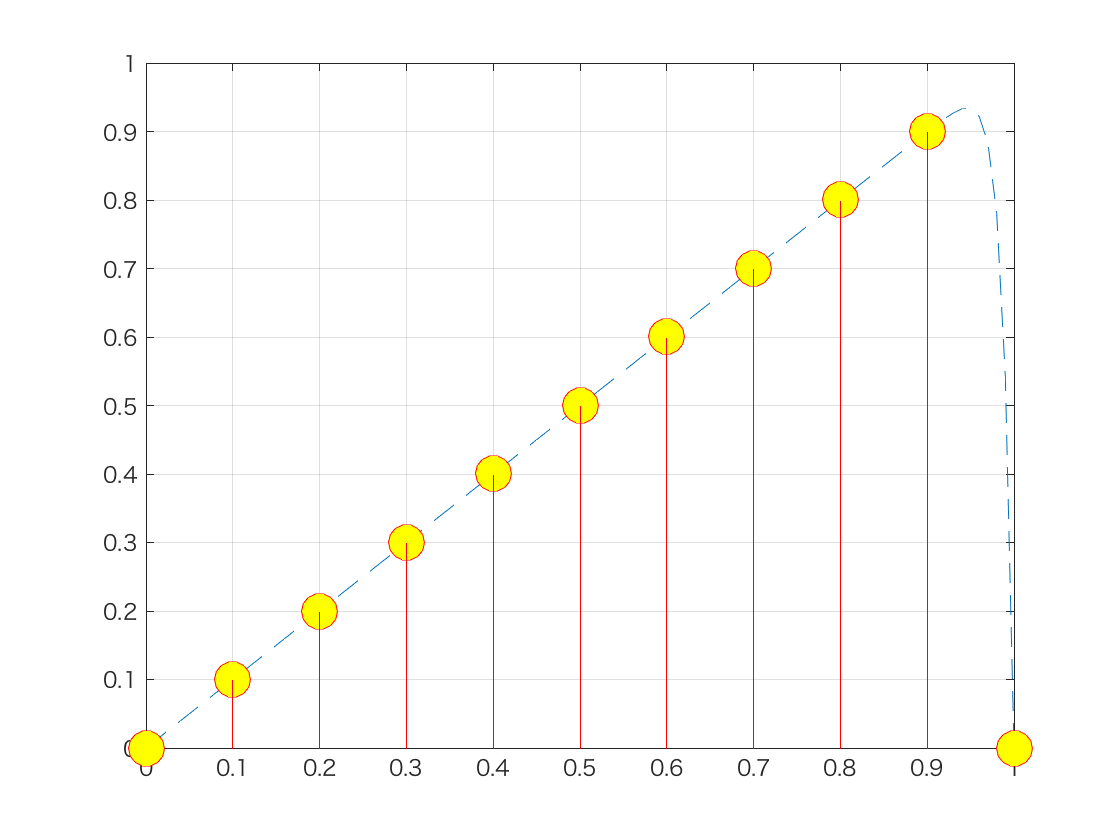
なお点線はもとの80次多項式曲線を表しています．

この11点のデータだけから，もとの80次多項式（点線）を推定しなさい，というのがここでの問題です．

MATLAB で解いてみよう

上の問題をMATLABで解いてみましょう．

まずは，多項式の定義から．多項式の係数からなるベクトルを定義します．

%% polynomial coefficients
x_orig = [-1,zeros(1,78),1,0]';

ここで，zeros(1,78)は1行78列（横ベクトル）のゼロだけのベクトルです．$-t^{80}$と$t$の間の係数はすべて0であることに注意してください．

この多項式から，11点のデータを生成します．

%% sampling
t = 0:0.1:1;
y = polyval(x_orig,t);

polyvalはMATLAB関数で，多項式の係数ベクトルから，多項式の値を計算する関数です．

10次多項式によるカーブフィッティング

まずは，11点を通る10次多項式を求めてみましょう．

%% Vandermonde matrix
Phi_v = vander(t);
%% Interpolation polynomial with order 10
x_i = inv(Phi_v)*y';

ここで，vander(t)というのは，ヴァンデルモンド行列と呼ばれる行列で，これの逆行列を観測データに掛ければ，補間多項式の係数が出てきます．

詳しくは，書籍「スパースモデリング」の第2.1.2節をご参照ください．

グラフを表示してみましょう．

%% Plot
tt = 0:0.01:1;
figure;
plot(tt,polyval(x_i,tt),'-');
hold on
plot(tt,polyval(x_orig,tt),'--');
stem(t,y);

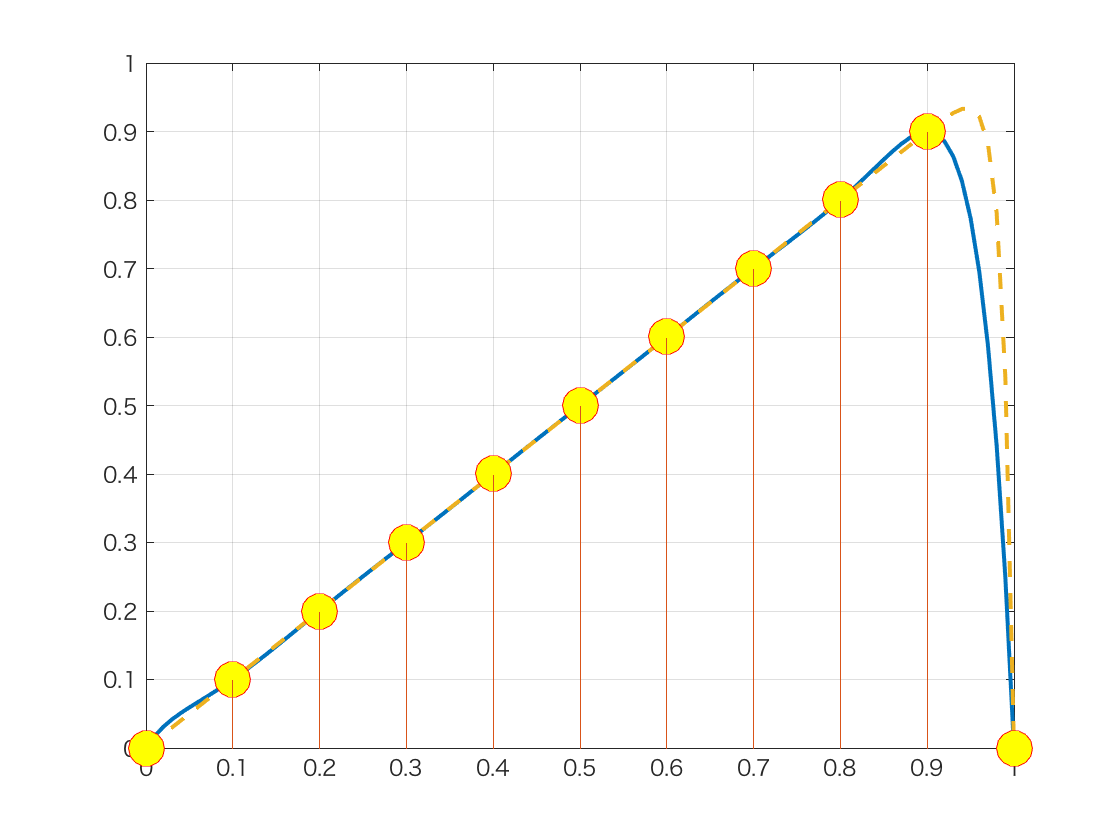
特に，t=0.9〜1.0の間で，もとの80次曲線とずれてしまっています．

スパースモデリングによる方法

では，スパースモデリングのテクニックを使って，80次曲線を求めてみましょう．

まず補間条件（求める曲線が与えられた点の上を通るための条件）を求めます．

% Order of polynomial
M_l = 80;
% Vandermonde matrix
Phi_l=[];
for m=0:M_l
 Phi_l = [t'.^m,Phi_l];
end

11点から80次多項式を求めるために，ヴァンデルモンド行列は$11\times 81$の横長の行列になっていることに注意してください．横長の行列なので，当然，逆行列は存在しません．より詳しく言うと，連立方程式

\Phi_l x = y

には無数の解が存在します．（$\Phi_l$は$11\times 81$のヴァンデルモンド行列です）．

スパースモデリングは，上の等式を満たす無数の解の中から最もスパースなものを選びます．すなわち，非ゼロの係数が最も少ない多項式を見つけます．

CVXで解いてみましょう．

% CVX
cvx_begin
 variable x(M_l+1)
 minimize norm(x,1)
 subject to 
   Phi_l*x == y'
cvx_end

簡単に答えが得られて，

となります．１番目の係数（$t^{80}$の係数）が$-1$，８０番目の係数（$t$の係数）が$1$となりました．正確にもとの多項式を復元しています．

グラフを描いてみましょう．

%% Plot
tt = 0:0.01:1;
figure;
plot(tt,polyval(x,tt),'-');
hold on
plot(tt,polyval(x_orig,tt),'--');
stem(t,y);

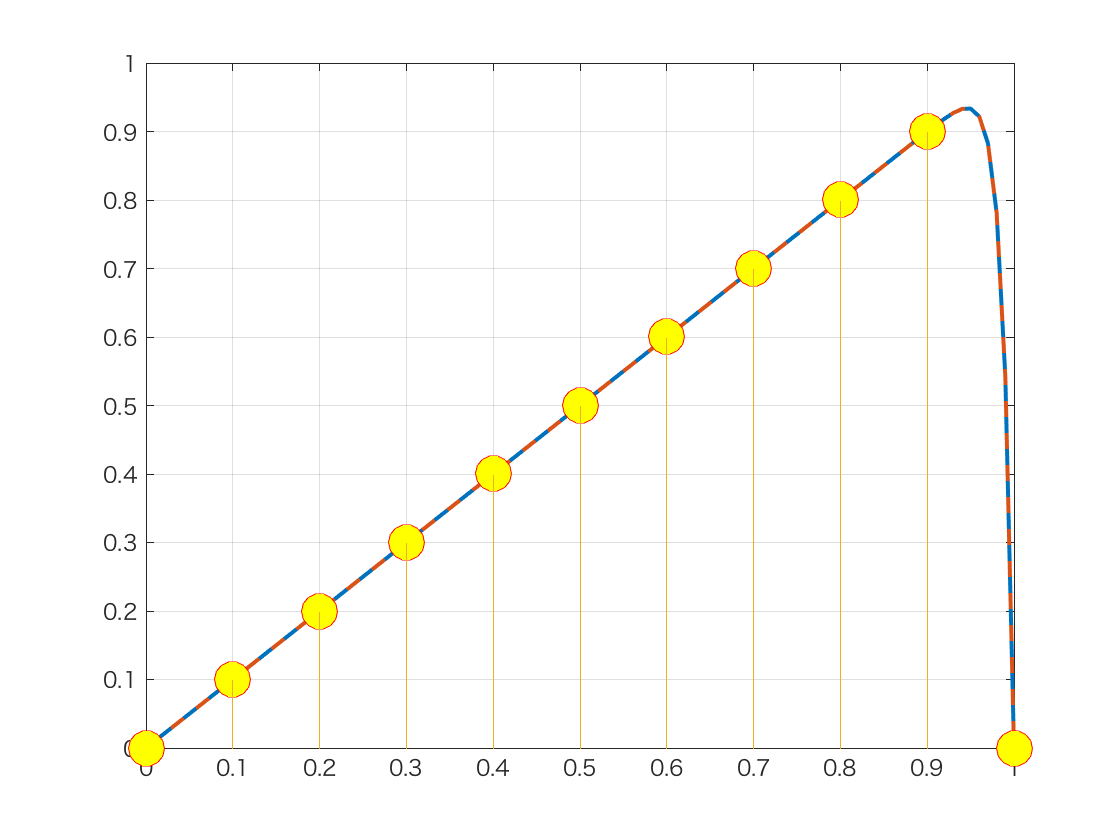
完全に一致しています．

スパースモデリングに興味を持った方は，ぜひ，書籍「スパースモデリング- 基礎から動的システムへの応用 -」でその仕組みを学んでください．

[出版社ページ](http://www.coronasha.co.jp/np/isbn/9784339032222/) [Amazonページ](https://www.amazon.co.jp/gp/product/4339032220/)

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up