はじめに
コロナ社から発行された本「スパースモデリング- 基礎から動的システムへの応用 -」の内容に関連することがらやMATLABコードについて，著者（永原正章）がわかりやすく解説します．
[出版社ページ](http://www.coronasha.co.jp/np/isbn/9784339032222/)
[Amazonページ](https://www.amazon.co.jp/gp/product/4339032220/)
スパースモデリングとは
最近，ディープラーニングがとても注目されています．データが大量にある場合（ビッグデータ），自動的に特徴量が抽出されるというのが，ディープラーニングの最も大きな利点でしょう．
しかし，それほど大量にデータが無い場合（スモールデータまたはミドルデータの場合）はどうすれば良いのでしょうか？本書で詳しく述べていますが，データが少ない場合，ディープラーニングのように学習パラメータが多いと，過学習（または過剰適合）が起き，学習がうまくいきません．
過学習を避けるためには，データの生成メカニズムを調べて，その性質を学習に組み込む必要があります．例えば，ある物体に電気を流して電圧と電流の関係を調べたいとしましょう．電圧と電流のデータが10組取れたとします．
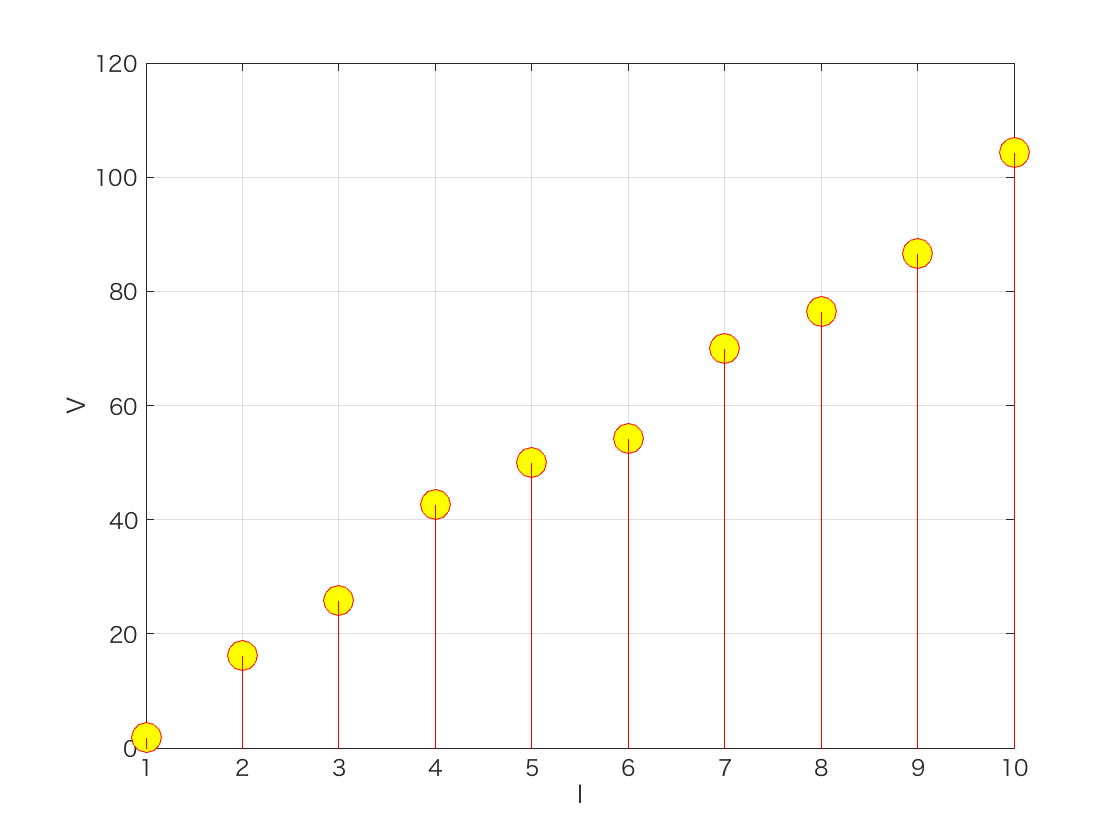
抵抗値は10Ωですが，少しノイズが乗っています．
これを何も考えずに学習（カーブフィッティング）してしまうと，９次補間多項式が出てきてしまいます．
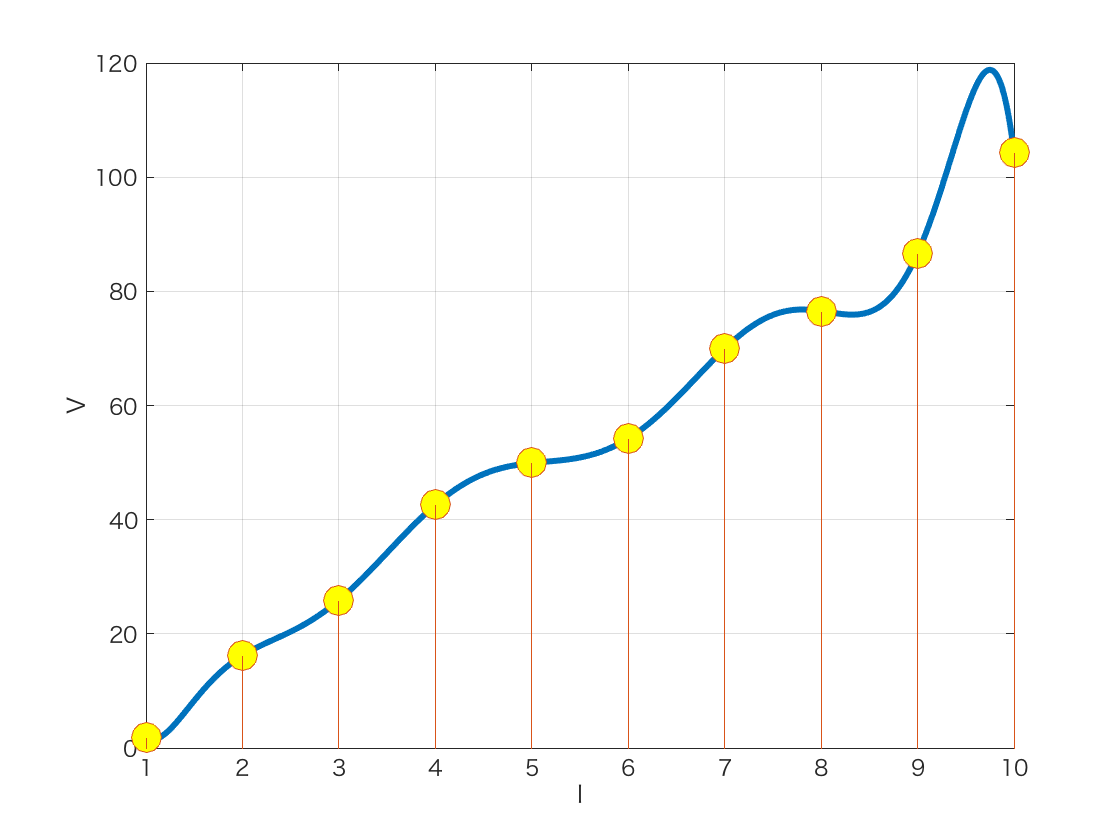
しかし，我々はオームの法則を知っています．データが電流と電圧の関係なら，はじめから１次式と仮定して，パラメータを傾きと切片の２つに限定して学習（最小二乗法というものを使います）すればうまくいきます．
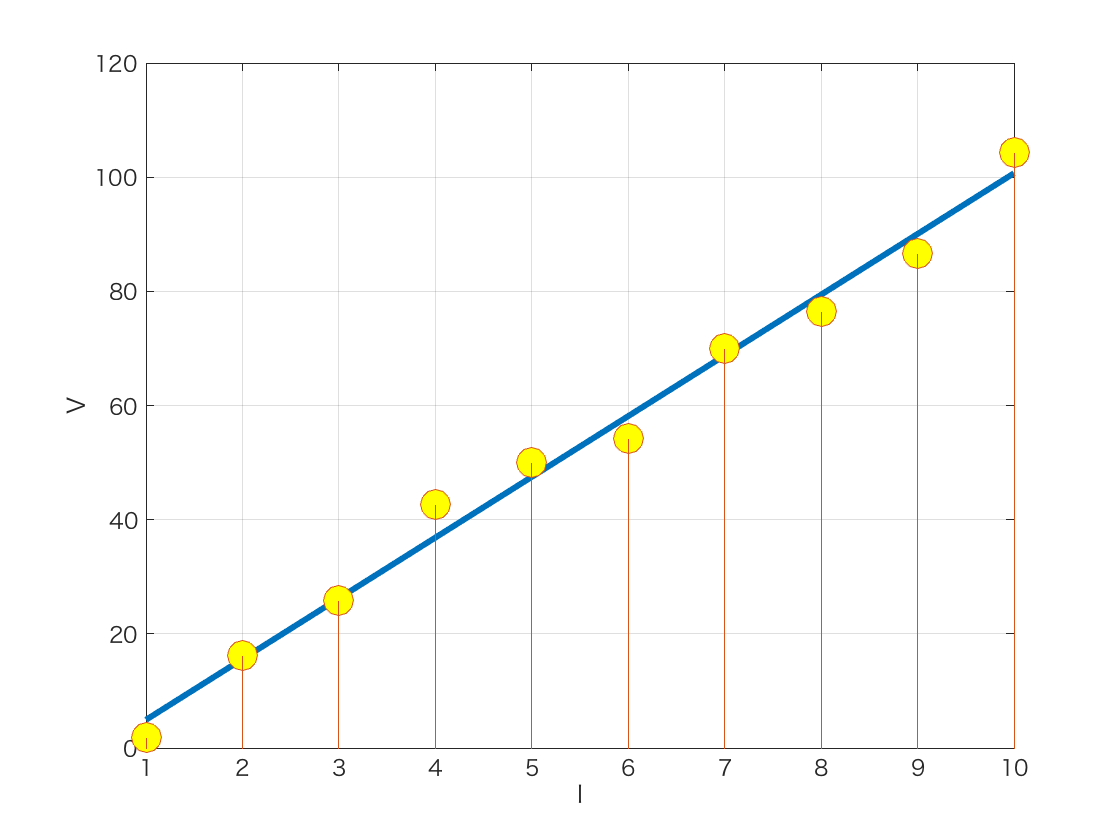
さて，世の中にはデータの生成メカニズムがよくわからない場合のほうが多いと思います．メカニズムがわからないから，データ分析をしたいということがほとんどだと思います．生成のメカニズム（およびノイズの性質）について何も情報がなければ，できることはデータ数と同じだけのパラメータを用意してフィッティングするしかありません．しかし，それでは過学習が起きてしまいます．
そこで，オッカムのカミソリという考え方があります．
同様のデータを説明する仮説が二つある場合、より単純な方の仮説を選択せよ．
というものです．「より単純な」というのは「よりパラメータが少ない」と解釈して良いでしょう．**スパースモデリングはこれを自動的に行います．**データから，自動的に重要なパラメータを選択してくれます．ですので，スパースモデリングでは，データ数に比べて大量の学習パラメータをあえて用意して，パラメータの自動抽出を行うことによって，単純で過学習を起こさないモデルを得ます．魔法のような方法ですね．
ディープラーニングとスパースモデリングの違いをまとめてみましょう．
- ディープラーニングは自動的に特徴量を抽出する
- スパースモデリングは自動的に学習パラメータを選択する
注：特徴量は基底または辞書とも言います．特徴量の抽出と学習パラメータの選択を
同時に行う方法もあり，スパース辞書学習 (sparse dictionary learning) と呼ばれています．
上の抵抗値のシミュレーションを行うMATLABコードです．
%%%% 電流と電圧の関係
%% 初期化
clear
%% データ生成
I = 1:10; % 電流
V = 10*I; % 電圧（抵抗値=10）
%% ノイズ
n = randn(1,length(I))*5; % 平均0, 標準偏差5のガウスノイズ
Vn = V + n; % 電圧データにノイズを付加
%% 補間多項式
A = vander(I); % ヴァンデルモンド行列
p = inv(A)*Vn'; % 補間多項式の係数
%% 最小二乗法
Al = A(:,end-1:end);
p2 = inv(Al'*Al)*Al'*Vn';
%% グラフ表示
II = I(1):0.01:I(end);
VV = polyval(p,II);
VV2 = polyval(p2,II);
figure;plot(II,VV); %補間多項式
hold on
stem(I,Vn);
figure;plot(II,VV2); %最小二乗法
hold on
stem(I,Vn);
#ディープラーニングとスパースモデリング
ディープラーニングとスパースモデリングの違いは
- ディープラーニングは自動的に特徴量を抽出する
- スパースモデリングは自動的に学習パラメータを選択する
でした．これをもう少し詳しく解説しましょう．
ディープラーニングは大量のデータから特徴量を自動的に抽出します．スパースモデリングでは，それほど多くないデータから学習パラメータを自動的に選択します．より少ないデータから学習できるのなら，スパースモデリングのほうが良いのでは？と思うかもしれません．
スパースモデリングでは，代わりに多数の特徴量（基底ベクトル）の候補を準備する必要があります．特徴量をあらかじめ決めておく必要のないディープラーニングとは正反対ですね．特徴量がたくさん準備できる場合，スパースモデリングは有利です．
また，ディープラーニングとスパースモデリングの間には，もう一つ，大きな違いがあります．スパースモデリングは線形モデル（パラメータが線形に依存する）なのに対して，ディープラーニングは活性化関数により非線形となることです．この非線形関数は以下の形をしています．
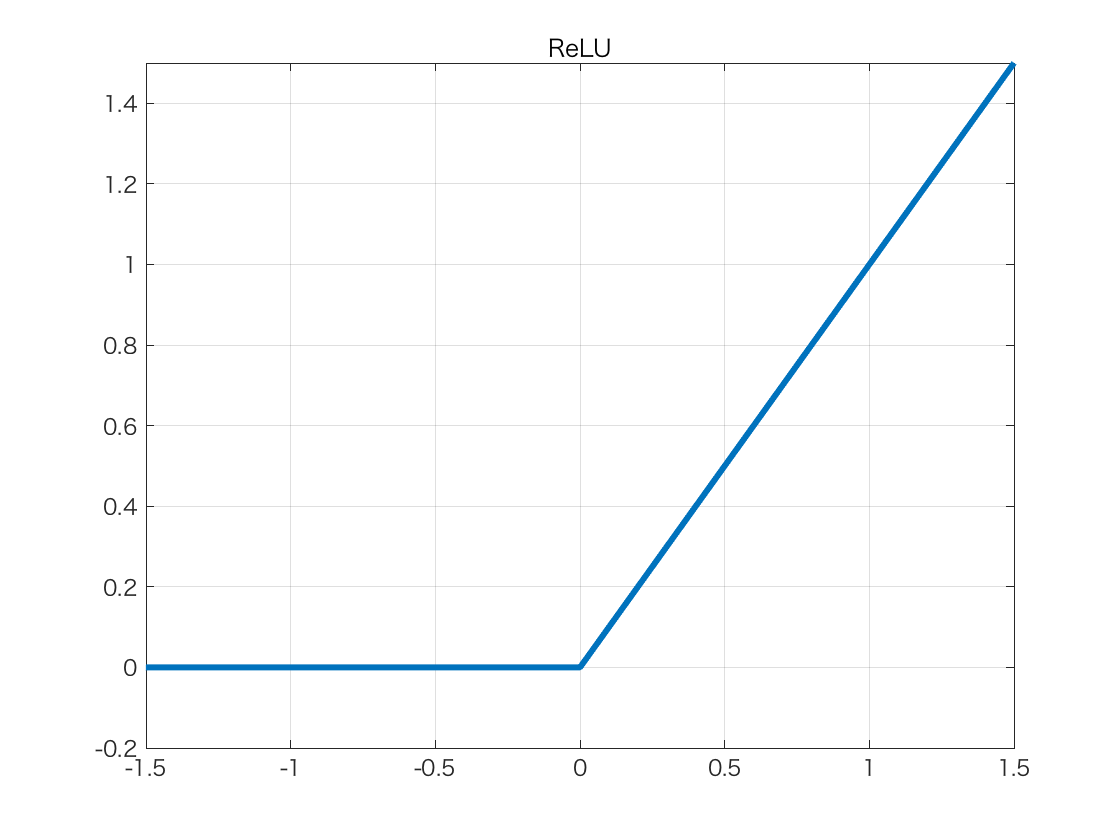
明らかに，この非線形性がディープラーニングの不思議な学習能力の源です（そして，ディープラーニングの数理的解析を難しくしている原因でもあります）．
まとめましょう．
- ディープラーニングでは大量のデータが必要
- スパースモデリングでは多数の特徴量（基底ベクトル）の候補が必要
- スパースモデリングは線形，ディープラーニングは非線形
#基底ベクトルと辞書
特徴量と基底ベクトルの話が出てきましたので，スパースモデリングで最も重要な概念である**冗長な辞書**のお話をしましょう．冗長な辞書とは，多数の特徴量の候補からなる集合のことです．
まず，基底ベクトルから．
線形代数で習ったことを思い出してください．N次元空間にはN本の互いに独立なベクトルが必ず存在します．
例えば，3次元空間では
$$
e_1 = (1,0,0),
e_2 = (0,1,0),
e_3 = (0,0,1)
$$
という3本の独立なベクトルがとれます．3本はこれに限らず，例えば
$$
f_1 = (1,1,0), f_2 = (1,0,1), f_3 = (0,1,1)
$$
も独立なベクトルです．
このように次元ど同じ数の独立なベクトルのセットを**基底**と呼びます．すなわち，{$e_1$,$e_2$,$e_3$} や {$f_1$,$f_2$,$f_3$} は3次元空間 $R^3$ の基底となります．
さて，つぎのベクトルの集合を考えてみましょう．
$$
{e_1,e_2,e_3,f_1,f_2,f_3}
$$
6本のベクトルからなるこの集合は$R^3$のベクトルを表現するのには冗長です．このようなベクトルの集合を**冗長な辞書**と呼びます．
「冗長な辞書」とは，たいへんうまいネーミングだと思います．
英語は2000語あれば話せるといいます．ですので，2000語の辞書で十分です．しかし，2000語の辞書に掲載されている単語だけから文章を作るとなると，かなり長くなってしまうでしょう．いっぽう，100万語の辞書から単語を自由に使って良いとなると，表現はかなり簡潔になります．これが，まさに**冗長な辞書からのスパース表現**なのです．
スパースモデリングとは，冗長な辞書から適切な単語（ベクトル）を自動的に選んできて，短い文章を組み立てる，そのような仕組みだといえます．「自動的に選んでくる」のは，辞書が膨大になればなかなか大変ですが，それを即座に計算する方法が近年開発され，コンピュータの高速化とあいまって，情報分野のホットトピックとなっているのです．
書籍「スパースモデリング- 基礎から動的システムへの応用 -」には，その詳細が記述されています．ぜひ手にとって確認してみてください．
[出版社ページ](http://www.coronasha.co.jp/np/isbn/9784339032222/)
[Amazonページ](https://www.amazon.co.jp/gp/product/4339032220/)