random rotation decision tree, simulated annealing decision tree

　今回はOblique DTの派生である、random rotation decision treeとsimulated annealing decision treeを紹介します。今回は非常に短いです。

random rotation decision tree

　これまた非常に簡単で、通常のDTへの入力をそのまま使うのではなく、Random Rotationを施してから分割するだけです。完

random rotation matrix

　これだけで終わるのももったいないので、random rotation matrix の生成について解説します。参考にした論文は下記のものです。
http://article.sapub.org/10.5923.j.ajcam.20170702.04.html
　アルゴリズムは非常に簡単なもので、

N次元のそれぞれ異なるランダムベクトルを2つ、XとYを作成する
それぞれのベクトルをいずれかの軸（論文中では第１軸）に平行に変換する行列、MxとMyを求める
Myの逆行列とMxをかけたものを求める
以上です。

2次元の場合

　解説が必要なのは上記の２の部分のみのため、こちらの詳細を解説します。最も簡単な２次元のベクトルを考えます。

X = 
\begin{pmatrix}
a  \\
b  \\
\end{pmatrix}, 
Y = 
\begin{pmatrix}
c  \\
d  \\
\end{pmatrix},

このベクトルを以下のように変換する変換行列$M_X, M_Y$を定義します。

\widetilde{X} = 
\begin{pmatrix}
\sqrt{a^2+b^2}  \\
0  \\
\end{pmatrix}
= M_X
\begin{pmatrix}
a  \\
b  \\
\end{pmatrix} \rm{with} ~~
M_X = 
\begin{pmatrix}
c_\theta & -s_\theta  \\
s_\theta & c_\theta  \\
\end{pmatrix}, ~~~
c_\theta = a / \sqrt{a^2+b^2}
\\

\widetilde{Y} = 
\begin{pmatrix}
\sqrt{c^2+d^2}  \\
0  \\
\end{pmatrix}
= M_Y
\begin{pmatrix}
c  \\
d  \\
\end{pmatrix} \rm{with} ~~
M_Y = 
\begin{pmatrix}
c_\phi & -s_\phi \\
s_\phi & c_\phi  \\
\end{pmatrix}, ~~~
c_\phi= c / \sqrt{c^2+d^2}

最終的に生成されるRandom Rotation Matrixは、以下で定義されます。

M = M_X^T M_Y

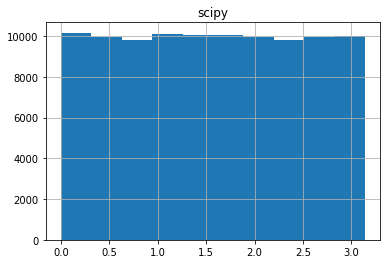
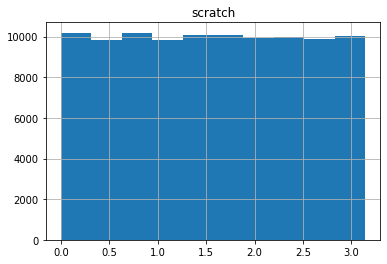
念のため、scipy.stats.special_ortho_group と、上記の計算方法で計算したものから計算された角度を比較してみます
（変換行列の(0,0)成分を$\arccos$で変換し、角度を求めました）。一様に分布していることがわかると思います。

3次元以上の場合

　基本的には３次元以上の場合においても手順は同様です。論文中では並列実行性にも言及していたため、簡単に触れておきます。

　最も単純には、N次元目とN-1次元目の間で処理を行い、次にN-1次元目とN-2次元目の間で処理を、という風に続きます。
並列実行は、例えば８次元のベクトルの場合には、

1次元目と2次元目, 3次元目と4次元目, 5次元目と6次元目, 7次元目と8次元目ごとに変換を行う
1次元目と3次元目, 5次元目と7次元目ごとに変換を行う
1次元目と5次元目で変換を行う
という風に進められます。段階の処理は完全に並列に進められるため、並列実行ができるという具合です。
ただ、論文中には実際の処理時間などについての記載はありませんでした。私も実装してみましたが、特にうまくいきませんでした。

simulated annealing decision tree（SADT）

　その名の通り、分割条件を決める際にsimulated annealing つまり焼きなまし法を用いるものです。こちらは広く一般的に知られているものかと思いますので、詳細な解説は割愛いたします。係数と切片をランダムに変化させ、既定の温度やIteration数などに達した場合に処理を停止します。

　文献を読んでいて面白いと思った点は、確か1997年ごろのものでRandom Forestが発表される前でした。文献中には単純にDecisionTreeを構築しても、ほぼ同じものしかできないため、アンサンブルの意味がないというような趣旨の記載がありました。今であればBagging、RandomSubsapceなどは簡単に思いつくものです。また、Oblique Splitなので当たりまえかもしれませんが、複数のSADTをいくつも作成し、最も小さい＝ノードの数が少ないSADTが最も精度が良かったという風な記載もあったと思います。どの文献か忘れてしまったため、現在捜索中です。

4. random rotation decision tree, simulated annealing decision tree