16. Nearest Neighbor Search

Nearest Neightbor Search：近傍探索

　次は近傍探索に関してです。近傍探索はその名前の通り、あるデータの集合の中から、クエリに近いデータを探し出す問題です。近いを定義するための距離の定義はいろいろありますが、ここでもユークリッド距離だけを扱います。近傍のサンプルの取得に関しては、近い順にN個とる方法と、クエリを中心とする半径R中の球に内部にあるサンプルをとる方法の二つがあります。
　近傍探索に対応して（？）、近似近傍探索という分類もあります。（おそらく）データ保存媒体が安価になってきたために、とりあえずデータを保存するようになってきて、近傍探索アルゴリズムでは対応しきれなくなってきた面があると思います。メモリーに載せきれなくなってきたり、特徴量数が多くなってしまいKDTreeやBallTreeでは対応できない領域が増えてきたのではないでしょうか。近似近傍探索はデータの圧縮や距離計算の簡略化などを行い、より大きいデータでも高速に近傍抽出できるようになることを目指しています。

基本的なアルゴリズム: Brute-Force, KDTree, BallTree

　最も基本的な3つの近傍探索アルゴリズムを紹介します。

BruteForceSearch

　最も単純な総当たり探索アルゴリズムです。データを事前に入力しておき、クエリが投入された際に、データとクエリの全組み合わせの距離を計算することで近傍を抽出することができます。Kmeansの記事でのように距離計算はGEMMを使って高速化しましょう。

KDTree

　BallTreeに並んで単純なアルゴリズムだと思います。Treeと名前がついている通り、空間を分割し階層構造を作成します。決定木の可視化と似たようなイメージです。したがって木の成長（＝学習）に関しては決定木と似たような感じで実装することができますが、いくつか変更しなければならない点があります。

• 親ノードから子ノードのつながり（ポインタ）だけでなく、子ノードにも親ノードのポインタを持たせる
• 分割点は中央値

決定木では上から下へ（根ノードから葉ノードへ）しか移動しませんでしたが、KDTreeではさかのぼる必要が出てきます。予測ではなく探索のためのアルゴリズムのため、木の成長が片方へ偏ることは探索時間が増加してしまうため好ましくありません。そのため、分割後の左右の子ノードのサンプル数が同じになるように中央値で分割をします。

　近傍抽出時も途中までは同じです。下記は近傍N個を抽出する場合で記載します。半径R中のサンプル抽出の場合は適宜読み替えてください。大体の関数は再帰関数で実装すれば簡単だと思います。

1. クエリを投入
2. アサインされる葉ノードを見つける（ここまで決定木と同じ）
3. 現在の葉ノード中にあるサンプルを近い順にN個、N個未満であればすべて保持する（同時に距離も保持する）

ここまでが第1段階です。残りは親ノードへさかのぼりつつ、その兄弟ノードとその子ノード（サブツリー）を調べていきます。まずは親ノードへさかのぼりつつ、兄弟ノードを調べるかどうかの判定部分についてです。

1. 自身の兄弟ノードを調べるために、親ノードへさかのぼる
2. クエリから親ノードの分割平面までの距離Aと、クエリが現在保持しているサンプルの中で最も遠いサンプルまでの距離Bを比較
   1. A>Bであれば兄弟ノードを調べる必要がないのでさらに親ノードへさかのぼる
   2. A<=Bであれば兄弟ノードを調べる。兄弟ノードに子ノードがあればそれもすべて調べる

ここで行っているのはクエリが保持するサンプルで形成される球と、分割平面が交わっているかどうかです。交わっていれば球の内部に兄弟ノード側のサンプルが含まれている可能性があるためです。本来は分割された直方体の頂点とクエリまでの距離を測ればよいと思うのですが、判定方法がわかりませんでした。分割平面までの距離と書いていますが、実際の実装は交わっているかどうかの判定はできていません。分割された直方体の面とは交わっていないため、スキャンする必要のないサブツリーをスキャンしている必要があります。

　つづいて兄弟ノードの調べ方についてです。

1. 兄弟ノード分割平面とクエリが形成する球が交わるかどうかの判定を葉ノードにたどり着くまで行う
   1. 交わっていれば子ノードはどちらも調べる。ただし、クエリが近い側のノードから調べる。
   2. 交わってなければクエリが近い側のノードのみ調べる
2. 葉ノード内のサンプルと距離計算を行い、保持しているサンプルとも合わせて近いものをN個保持する。

以上のような操作を行うことでKDTreeを実装することができます。探索部分のみ簡単な例でみてみましょう。右側の青い点がサンプルで、黒いQとなっている点がクエリとします。実際は各分割線上にもサンプルが配置されるのですが、ここでは無視しています。左側の木の四角のノードが葉ノードで、各色は右側の領域と対応しています。

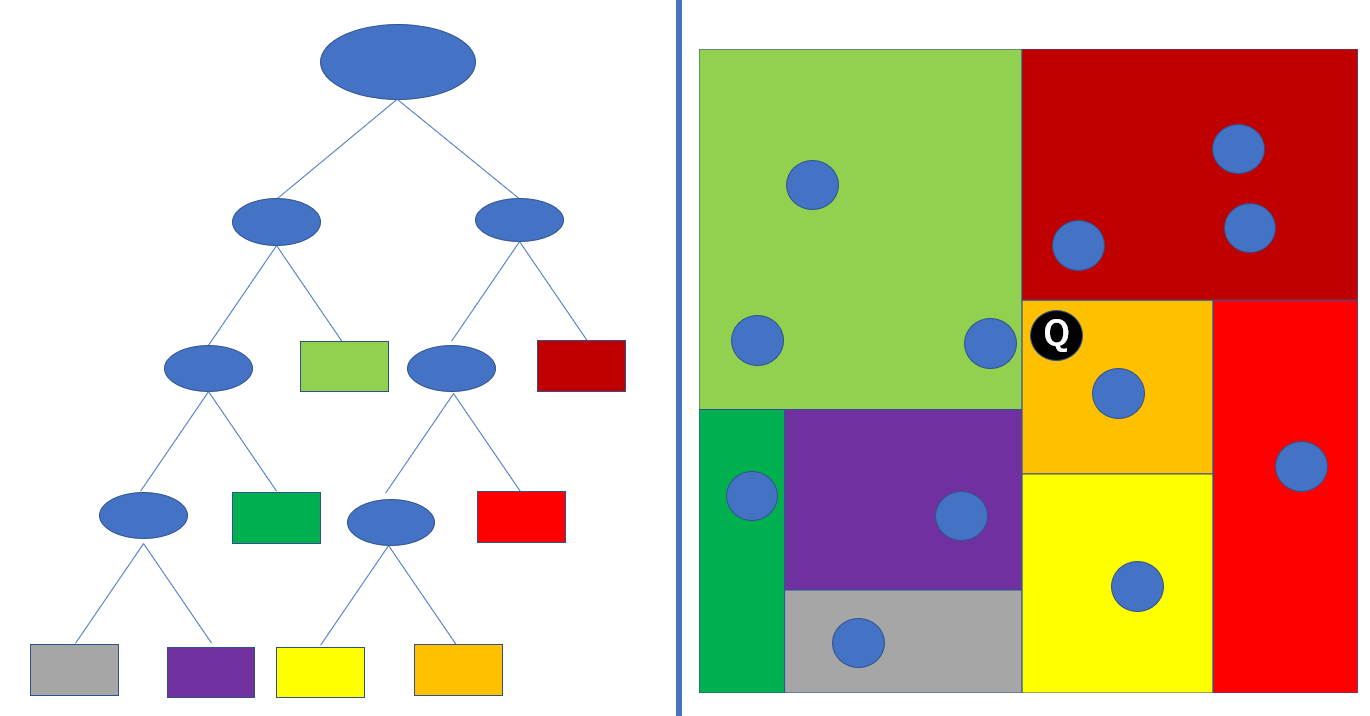
近傍3個のサンプルを取得する場合を考えます。2次元平面状では一目瞭然で選ぶことができますが、KDTreeの手順に従ってみていきましょう。

1. クエリが属するオレンジノード内のサンプルは1個のため、保持します
2. 次に兄弟ノード（黄色ノード）を見に行きます。この時保持しているのは1個のサンプルが形成する球と黄色ノードの分割平面は交わっていませんが、3個の近傍を取りにいかなければならないため、スキャンする必要があります。ここでも1個しかないので黄色ノードのサンプルを保持します。現在2個です。指定した近傍数を下回るか、ダミー近傍サンプル（距離無限大）で埋めておくのもよいかもしれません
3. さらに親ノード（オレンジ＋黄色＋赤）にさかのぼります。現在保持しているのは2個なので、赤ノード内のサンプルも保持します。現在3個保持しています。
4. さらに親ノード（オレンジ＋黄色＋赤＋濃赤）にさかのぼります。現在保持している3個のサンプルが形成する球は明らかに濃赤ノードとの分割平面と交わっているため、スキャンする必要があります。また、濃赤ノードは葉ノードであるため、サブツリースキャンは必要ありません。濃赤ノード内の全サンプルとクエリとの距離を計算し、近いものを3個保持します。微妙ですが、今保持しているサンプルはオレンジ1個、濃赤2個でしょうか。
5. さらに親ノードにさかのぼります。分割平面（右図の真ん中の直線）とクエリの形成する球は交わっているので、木の左側をスキャンする必要があります。
6. 最もクエリに近い薄緑ノードから見てみます。濃赤ノードと同じように距離計算を行い、保持するサンプルと合わせて3個近傍を保持します。オレンジ、濃赤、薄緑1個ずつです。
7. 続いて薄緑ノードの兄弟ノード（緑＋紫＋灰）のサブツリーを見ていきます。この兄弟ノードとクエリの形成する球は交わているので、スキャンの必要があります。兄弟ノード（緑＋紫＋灰）の分割平面（緑と紫＋灰を分けている平面）はクエリの形成する球と交わらないため、スキャンの必要がありません。
8. 残った紫＋灰に関しても同様に、紫と灰を分ける平面とは交わらないため、灰ノードはスキャンする必要がありません。紫ノードは一応スキャンしなければならないので、距離を計算しますが、現在保持する3個より遠方にあるため、保持は行いません。

非常に細かい点

　KDTreeでもKmeansで実装した距離計算の高速化が使えると思います。実際にFortLearnerではそのようにしています。ただしこれは葉ノードのサンプルがあまり小さいと意味がありません。比較的大きな値（32とか64）にしなければなりません。行列計算のオーバーヘッドが大きくなるからです。追加の恩恵としては少しですが、Treeの形成時間も速くなっているはずです。

KDTreeに関しては以上です。

BallTree

　次はBallTreeに関してです。個人的にはKDTreeより簡単に実装できた気がします。KDTreeとサンプルを階層的に分割して構造を形成する点は同じですが、平面で分割ではなく、各ノードのサンプルが含まれる球を再帰的に形成していきます。さらに簡単に感じた点としては、近傍探索時に再帰関数で途中の分岐から始めればよかったので、親ノードにさかのぼる必要がなかった点です。

構築

　データの2分割を繰り返すという点では、KDTreeと特に変わる点はありません（BallTreeのノードはボールと言い換えます）。少しだけ違う点でいうと、

• KDTreeのノードはデータの存在する領域をノード自体が保持しないが、BallTreeのボールはすべてのデータを含む領域を中心とデータすべてを含む半径として明確に保持する。

があるかと思います。KDTreeでは探索時に現状保持しているサンプルが本当にTop N個の最近傍であるかの判定が少し面倒でしたが、BallTreeは上記のような点があるため、若干その判定が簡単になったような気がしました。したがって、BallTreeの構築は、以下を行います。

1. データを投入
2. データの重心と重心から最も遠いサンプルまでの距離を計算、ボールを作成
3. データを２分割し、子ボールを作成
4. ２と３を繰り返す

ここで、データの分割はいくつかあります。性能はデータの分布に依存するので、適宜調整が必要です。

1. 深さごとに順番に特徴量を一つだけ選ぶ
2. 最大最小の差が最も大きい特徴量を一つだけ選ぶ（分散が大きいではない）
3. PCAを実行し、第１軸に沿って分割を行う

検索

　検索時は比較的簡単です。再帰関数を用いてDepth-First Searchを行うだけです。

1. クエリを投入
2. 根ボール（根ノード）の２つの子ボールの内、クエリに近いほうから先に探索
3. 葉ボール（葉ノード）まで行きついたら、KDTreeと同じ操作で現在のボール内の近傍サンプルをN個取得。

再帰関数の途中から探索再開します。

• こちらもKDTreeと同じくクエリが保持するサンプルが形成する球と未探索側の球が重なっていたら、子ボールを探索する

を条件として葉ノードまで行きついたらまた現在保持するサンプルと合わせてN個の近傍を再度選択することを繰り返すだけです。

以上