SVM
Support Vector Machineについての解説です。こちらもとりあえず実装したもので、突っ込んだ解説ができそうにありません。また、最適化も全くできていないため、非常に低速です。libsvmがsklearnでも用いられているようなので、これらのPDFを参考にしつつ最適化や機能の拡張(Regression、One-Class SVMなど)をしていこうと思っています。
個人的には面白くて好きなアルゴリズムですが(一度仕事で利用して想定外に良い結果が得られました)、比較的計算量が大きいので最近はあまり用いられていない印象です。リソースが限られている(~GPUがない)ならばRandomForest、GBDTなどを使い、十分にあるならばDeepLearningを使えばいいみたいな感じでしょうか。もちろんすべての問題に適用できる銀の弾丸は存在しないので、人間がうまく使うことができればきちんと成果を出すことができます。
ハードマージン、ソフトマージン
資料として機械学習のエッセンスを参考にさせていただきました。式変形をほぼ記載しているため、非常にわかりやすかったです。ただ、ここまでやりたい人にはPythonの基礎的な文法はいらないのでは?と思いました。個人的にはもう少しいろんなアルゴリズムが乗っている方がうれしかったです。
分類問題では分離超平面を学習します。このときすべて分離(=超平面のそれぞれの側でクラスが完全に分離できている状態。多クラス分類の場合は、ある一つのクラスとその他すべてのクラスに分離)できている状態になることは現実世界のデータセットでは非常にまれです。これは、そもそも特徴量が足りないか、問題がノイズを含んでいるような場合だと思います。
下図のような状態が考えられます。左は完全分離可能、右は分離不可能(困難)な状態です。それぞれハードマージン、ソフトマージンと呼ばれるものをマージンの最大化を行います。ここではとりあえず、LinearSVMを主に見ていきます。Kernelを考える場合でもほとんど同じようにできるはずです。
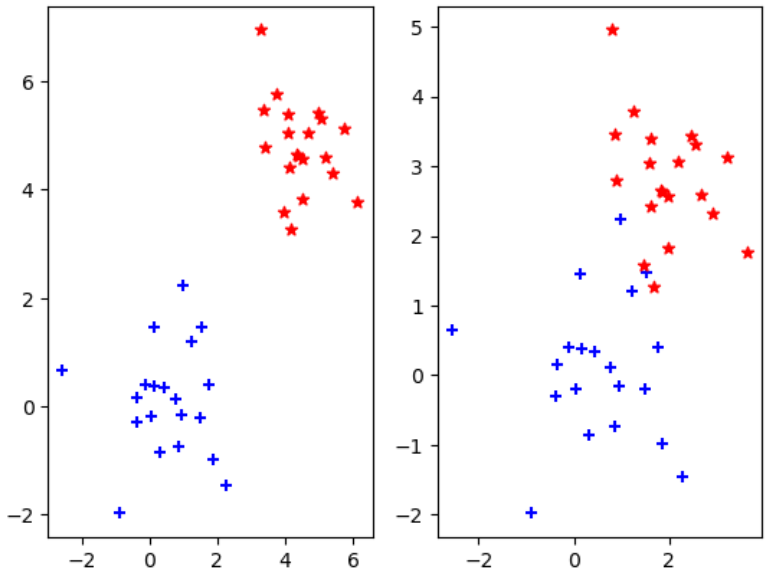
ハードマージン
まずはハードマージンから考えてみます。このような場合は空白部分を通るような直線を引けば完全に分離が可能です。しかし、その中で本当に欲しいものは、「新しいデータが来た際も正確に分類できる直線」です。今度は「新しいデータが来た際も正確に分類できる直線」とはどのような状態化が気になります。直感的には、二つのデータの真ん中らへんをうまく通るような直線を引けばよいような気がします。

この定式化を考えてみます。ラベルはそれぞれに+1とー1を割り振ります。どちらのラベルをどちらに割り振るかは気にしないでよいと思います。この時、最大化したい目的関数は、もっとも直線までの距離の近い$x_i$を選び、かつ式の値が最大になるような$w_0, \boldsymbol{w}$を選択します。
\text{Maximize}_{w_0, \boldsymbol{w}} \text{min}_i \frac{y_i (w_0 + \boldsymbol{w}^T \boldsymbol{x}_i)}{||\boldsymbol{w}||}
\rightarrow \text{Minimize} \frac{1}{2} ||\boldsymbol{w}||
式変形をすべて追う時間がないので、いくつかの参考URLを載せます。
カーネル学習法
ソフトマージンのサポートベクターマシン(SVM)の解説 理論編
目的関数を変形すると最終的に下記が導かれます(ラグランジュの未定乗数法)。
\begin{align}
\text{Maximize} & \hspace{10pt} f(\boldsymbol{a}) = \sum_{k=1}^N a_k - \frac{1}{2} \sum_{k=1}^N \sum_{l=1}^N a_k a_l y_k y_l \boldsymbol{x}_k^T \boldsymbol{x}_l \\
\text{Subject to } & \hspace{10pt}
\sum_{i=1}^N a_i y_i = 0 \\
& \hspace{20pt} a_i \geq 0 \\
& \hspace{20pt} a_i \left\{ y_i (w_0 + \boldsymbol{w}^T \boldsymbol{x}_i) - 1 \right\} = 0
\end{align}
下三つの制約条件を満たしつつ、$f(\boldsymbol{a})$を最大化します。通常の2次計画問題ソルバーでもとけるようですが、Platによるアルゴリズムが単純であるため、ここでは見てみます。ただLibSVMでは、Fanらによるアルゴリズムが用いられているようです。今後きちんと見てみたいと思います。
単純には、
- $\boldsymbol{a}$ の内から二つの $a_i$ と $a_j$ を選び、最適な$a_i$ と $a_j$を求める
ことを繰り返すのみです。これも式変形を飛ばして、最終的にどう$a_i$ と $a_j$を計算すればよいかを見てみると
a_i = \frac{1}{||\boldsymbol{x}_i - \boldsymbol{x}_j||^2}
\left\{
1 - y_i y_j + y_i (\boldsymbol{x}_i - \boldsymbol{x}_j)^T
\left(
\boldsymbol{x}_j \sum_{k \neq i,j}^N a_k y_k - \sum_{k \neq i,j}^N a_k y_k \boldsymbol{x}_k
\right)
\right\} \\
a_j = y_j \left( -a_i y_i - \sum_{k \neq i,j}^N a_k y_k \right)
ただし、$a \geq 0$ という条件があります。最後に語のように$i, j$を選択すればよいかについてです。再度変形した後の$f$とその制約条件に対してラグランジュの未定乗数法を用いて、ゴニョニョしていくと、下記の条件を得ることができます。
\text{min}_{y=-1 \text{ or } a>0} y_t \nabla f(a)_t \geq \text{max}_{y=+1 \text{ or } a>0} y_t \nabla f(a)_t \\
\text{where } \hspace{20pt} \nabla f(a)_t = 1 - \sum_{l=1}^N a_l y_t y_l \boldsymbol{x}_t^T \boldsymbol{x}_l
左辺と右辺それぞれの条件を満たす$i, j$を求めることができるようになりました。そして、パラメータとしては$w_0, w$を計算したかったので、最初にラグランジュの未定乗数法を用いたときに$w$での微分が0であることと$y_i (w_0 + \boldsymbol{w}^T \boldsymbol{x}_i) - 1=0$が$a_i\neq 0$で成立するので、
w_j = \sum_{i=1}^N a_i y_i x_{ij} \\
w_0 = \frac{1}{N_{a \neq 0}} \sum_{k \in a \neq 0}\left( y_k - \sum_{k \in a \neq 0} a_l y_l \boldsymbol{x}_k^T x_l \right)
で求めることができます。
ソフトマージン
次にソフトマージンを考えてみます。二つのクラスが入り混じっているため、そのまま線を引くことができません。そこで少しだけ、目的関数に修正を加えます。本来あってほしい分離平面の反対にあるデータに対して、$\xi$ というパラメータを割り振ります。当然これは小さくあってほしいので、以下の式を最小化します。
\text{Minimize} \hspace{20pt} \frac{1}{2} ||\boldsymbol{w}|| + C \sum_{i}^N \xi_i
Cはどれほどこの誤りを許容するかのパラメータで、大きいほど誤りが大きくなります。小さくしすぎると訓練データに対して過学習するので、一定程度割り振っておく必要があります。パラメータが多くなったため、ラグランジュの未定乗数法が少し複雑になりますが、手続きとしては特に変更がありません。いくつか追加された条件を確認すると、
- aはC以下でなければならない。
- $i,j$ の選択の条件も
- i: $y=-1 \text{ or } a>0 \rightarrow (y>0 \text{ and } a>0) \text{ or } (y<0 \text{ and } a<C)$
- j: $y=+1 \text{ or } a>0 \rightarrow (y<0 \text{ and } a>0) \text{ or } (y>0 \text{ and } a<C)$
となります。$w, w_0$の求め方はとくに変更ありません。
カーネル
今までは分離超平面を考えていました。しかし実データには平面で分割できないものも存在します。分離平面から、分離曲面への変更を考えます。
w_0 + w x \rightarrow w_0 + w \phi(x)
ここで、$\phi$は何らかの関数です。これを用いると$f$が次のように修正されます。($K(x_i, x_j) = \phi(x_i)^T \phi(x_j)$)
\text{Maximize} \hspace{10pt} f(\boldsymbol{a}) = \sum_{k=1}^N a_k - \frac{1}{2} \sum_{k=1}^N \sum_{l=1}^N a_k a_l y_k y_l K(\boldsymbol{x}_k, \boldsymbol{x}_l )
ここで、$K$をカーネル関数と呼びます。$\phi$自体の形はどこかに行ってしまって、その二つの$x$を入れたときにどのように計算するかを定義すればいろいろな形の超局面の場合が計算できます。いくつか有名なものを記載します(参考 )。
\begin{align}
\text{RBFカーネル} & \hspace{10pt} \exp \left( - \frac{|x_i-x_j|^2}{2\sigma^2}\right) \\
\text{線型カーネル} & \hspace{10pt} x_i^T x_j \\
\text{多項式カーネル} & \hspace{10pt} (1+x_i^T x_j)^d\\
\end{align}
データの保存
線型SVMでは$w_0, w$のみを保存していました。一方カーネルSVMでは、一部のデータを保存しなければなりません。これは分離超局面を構成するために必要となります。とはいえすべてではなく、マージン付近のデータのみでよいので、そこまでメモリなどを気にする必要はないと思います。
高速化
機械学習のエッセンスを参考として実装しましたが、あまりコードを深く理解できていないので、まだ本文中にも記載のものしか見つけられていません。数百サンプル程度でも1分ほどかかってしまっています。
- 一度計算したカーネルの再利用
Plattによる最適化アルゴリズムからFanらによるものに移った段階でもう少し深く読み込んでみようかと思います。現状では1万程度でも数日かかりそうな状態です。