自動微分
話題としては最後になります。自動微分についてです。自動微分は、その名前の通り解析的に関数を微分しなくとも、関数自体の構造からその微分を計算する手法です。複雑な関数それ自体だけでも関数として定義できれば、より複雑になるであろう微分でも簡単に計算することができます。感覚的なものですが、微分すると複雑になることが多いと思います。整理すれば簡単になるかもしれませんが、整理することで計算ミスが入ってしまう可能性もあります。整理しないことで無駄に項の数が多く、符号や係数を間違って実装してしまうかもしれません。
しかしながら、深層学習(ほかの適用範囲でも?)では毎回のように微分を求めるわけにはいきません。非線形関数を多用しますし、if文での分岐が入るかもしれません。ここら辺に対応するためには、自動微分の技術を応用する必要があります。
解析解を用いない理由は、実験の速度とバグが理由であるのであれば、数値微分はどうでしょうか。こちらも用いられない理由があるとおもいます。まず一つはここでも速度だと思います。1変数関数の差分法では微分の近似値を求めるために、2回関数を計算しなければなりません。2変数関数では4回です。これは入力数が増えることが加速度的に増加していしまいます。機械学習分野では特に大量の入力が一般的なので適しません。
二つ目の理由は数値の精度に関してです。数値微分は微分を求めたい点から微小な数値分だけずらし、その値を利用して微分値を求めます。私も学生の時に始めて調べた際にすぐに微小な数値を小さくしすぎるとむしろ誤差が拡大してしまうというのを見た覚えがあります。深層学習で求める目的関数の微分は2次関数のように滑らかでないことが多く(非常に高次元のため可視化が難しいですが)いはずです。単純な差分法を使って求めるにはおそらく非常に小さい値を設定しなければならないので、これまた適用が難しくなります。その点自動微分は「正確」にほしい値を計算することができます。
これらの理由で、自動微分が用いられているかと思います。間違い、ほかの理由をご存じの方いらっしゃいましたら、文献等ご教示下さい。
FortranCommunityでもLfortranに自動微分の機能を導入できないかというような議論があったかと思います(ページが見つけられませんでした)。ASTをPythonなどで解析するというような感じだったかと思います。Fortranでも二つほど自動微分の実装を見つけることができました。
https://github.com/yizhang-yiz/fazang
https://github.com/zoziha/Auto-Diff
ただどちらもすこしづつ使いにくそうだなと思う点があったので、すこし個人的に改良(になっているかは疑問ですが)を加えてみました。あとで少し理由を記述してみます。
分類
本題に入る前に少し分類についての話を書いてみたいと思います。これで尽きていないとは思うのですが、自動微分を実装していて見つけたものを記載します。
Forward vs Backward
一番重要となる分け方かと思います。名前の通り微分を順方向で計算するか、逆方向で計算するかです。下記の図はWikipediaからの引用です。
f(x_1, x_2) = \sin(x_1) + x_1 x_2
という関数の自動微分を表しています。
Forward
Forward-modeの自動微分では、入力の内の一つを固定(画像では$x_2$をseedとして固定)し、伝播させます。
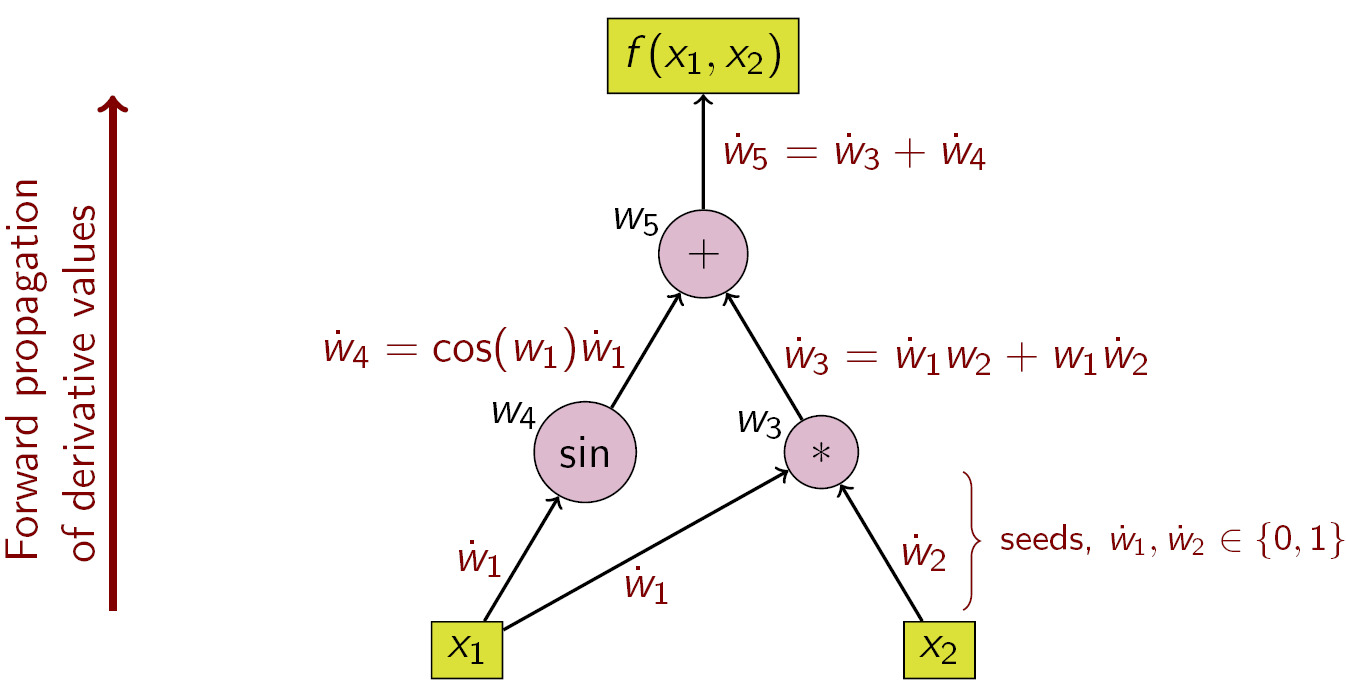
こちらの文献には別の関数の例とともに載っています。入力の$x_1$についても微分を求めたければ今度は$x_1$を固定して再度計算をしなければなりません。そのため、深層学習のように、Multi-Input→Single-Outputのような場合にはこちらは不適当です。例えば256x256x3の画像を入力すると約20万回計算する必要があります。もちろん画像の各ピクセルに対して微分を求める必要はなく、重みに対してのみのためここまでの回数はないかもしれません。しかし、VGGなどの古い(2014年、最近の深層学習の進歩を思えば十分に古いかと思います)モデルでは数千万パラメータはあるので、この分だけ計算をしなければならない、と思います。さすがにこれでは試す気が起きないので、もっと小さいモデルで試してみたいとは思います。
こちらのモードの適用範囲がよくわかっていないので、文献など教えていただけると嬉しいです。
Backward
Backward-modeの自動微分では、出力の内の一つを固定(画像では$f(x_1, x_2)$をseedとして固定)し、伝播させます。
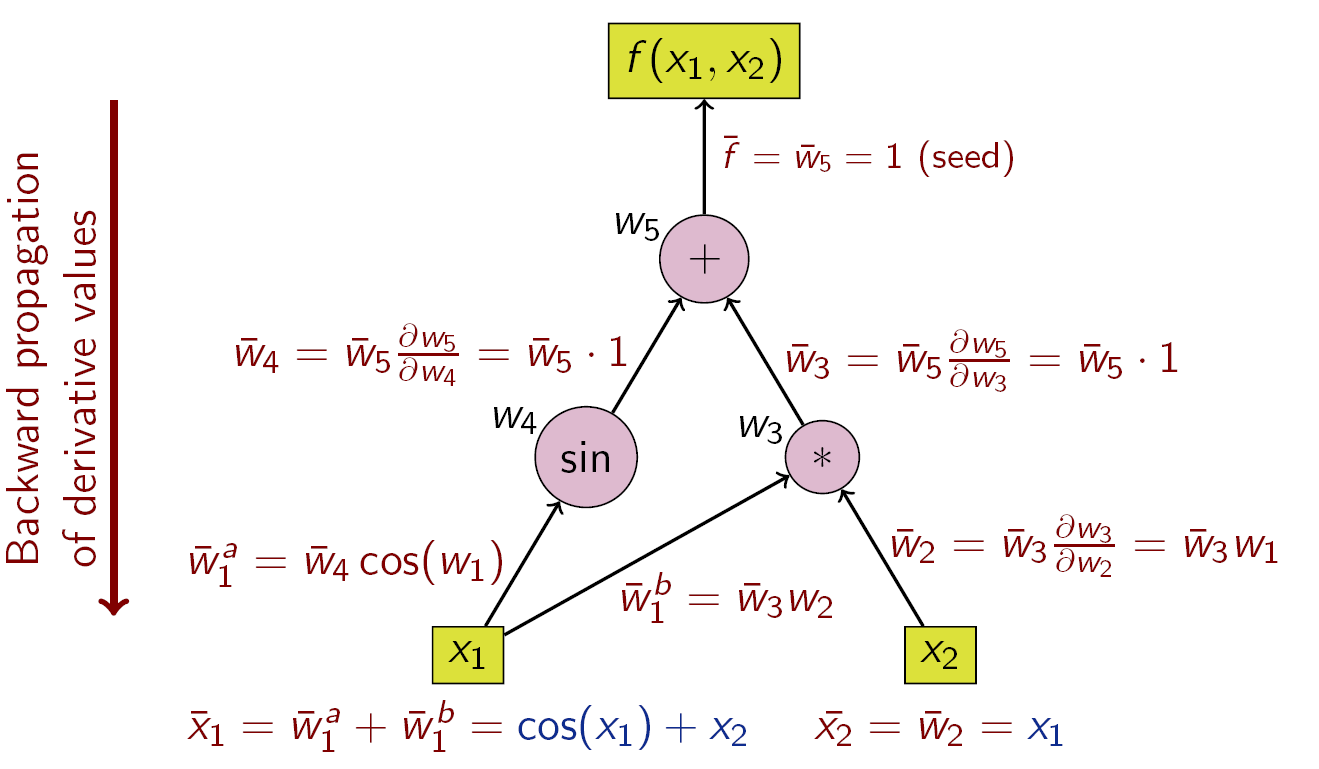
深層学習ではこちらが一般的(というかこれ以外に選択肢がない?)です。基本的に損失関数は何らかのスカラー値です。Multi-Task学習をするにしても。複数の損失関数を重みをつけてたしあわせます。当然FortLearnerでもこちらを採用しています。
ただ、実装としては圧倒的にForward-modeが簡単なように見えました。入力の内から一つを固定してループを回すのみで、複雑な関数を定義しても特に問題がなさそうに思えました。もしかしたら実装してみると意外な問題点があるかもしれません。
Graph vs Tape
前者はChainerやPytorch、新しい(といってももう新しいバージョンしかないと思いますが)Tensorflowです。後者はTensorflowでも用いられていたようです。
前者は、変数と関数自体がつながりを保持します。詳しくはゼロから作るDeep Learning ❸をご覧ください。細かいステップで記述されており、非常にわかりやすかったです。この本がなければ今でも実装できていなかったのではないかと思っています。
変数→関数→変数→関数
のようにそれぞれがつながりを持っており、Backwardの際にはこのつながりをさかのぼることでパラメータの更新が行われます。1巻が発売された直後くらいに、自分でも複雑な構造をもつネットワークを記述できるようなものを組んでみたいと思っていましたが、壁に当たってしまいました。個人的に最も実装がわからなかった点が、分岐がある場合の処理です。下記のように、途中から処理が分岐したときにどのように処理すればよいのかが全く思い浮かびませんでした。答えとしては各変数に「世代」を持たせることで、さかのぼり際に世代の大きい順に処理を実行すればよいことになります。
変数1 ---- 関数1 ----- 変数2 -----関数2
\ ----- 関数3 ----- 変数3
後者は変数自体ではなく、どこかべつの場所(Tape)にその順序を保存する手法です。Wengert-Listと呼ばれるものが有名かと思います。FortLearnerではこちらで実装しています。理由としては、GraphBaseで実装する方法が思いつかなかったからです。例えば、Pytorchでモデルを作成すると下記のように書けます(例なので、モデルとしては意味がありません)。
class MLP(nn.Module):
def __init__(self, in_dim, hid_dim, out_dim):
super(MLP, self).__init__()
self.linear1 = Dense(in_dim, hid_dim)
self.linear2 = Dense(hid_dim, out_dim)
def forward(self, x):
x = self.linear1(x)
x = relu(x)
x = self.linear2(x)
x = relu(x)
return x
一番問題としては、forwardの部分で、同じ関数名、同じ変数名の使いまわしができなかったという点です。もちろん毎回新しい変数を使用しても性能上は問題がないはずです。Backwardの際には結局Forwardでの計算結果も保持していなければならないからです。しかし、Fortranなので、新しい変数/関数は毎回定義しなければなりません。これは非常に面倒です。実験速度を速めるために自動微分を用いているのに台無しになってしまうくらいの気分でした(もちろん解析解を求めるよりはましかと思いますが、解析解はそもそも現実的ではありません)。xにreluのポインタを持たせることででつながりを保持するようにしたのですが、上書きが発生してしまい、失敗に終わりました。fazangはおそらくTape-Basedな実装になっていると思います。Auto-Diffは、Graph-Basedな実装になっていると思いますが、一つ問題があるかと考え実装しませんでした。それは、例えば行列積を計算する際に、行列全体を格納し積を計算するのではなく(=floatの要素を持つ行列)、行列の要素一つ一つが独立にライブラリ中で定義されたtypeを持つ変数に見えたからです。これが例えば行列積のBlasでの高速化、もっと単純にはコンパイラでの最適化が入る余地が少なくなるのでは?と思ったため実装を見送りました。多分うまいことやればFortranでもGraph-basedな実装ができるとは思います。
Tape-Basedで問題というほどではないですが、少し面倒な点がありました。それは二つ以上のネットワークを組み合わせる時です。Graph-Basedなら二つを単純につなげればよいはずです。しかしTape-Basedでは、二つのネットワークはそれぞれ別のテープに格納されています。一つに合わせたときに、どちらが主になったかがごちゃごちゃになってしまい少し苦労しました。
余談ですが、FortLearnerと名前をつけるはるか前にNeuralNetworkを実装しました。その時はみじんも誤差の逆伝播を理解していなかったので、逆伝播自体も自分で実装しなければならないものでした。Forward部分を変更すれば、Backwardで対応する部分はどこにあるのかを探す必要があって、毎回面倒でした。しかし、自動微分がどれだけ恩恵のあるものかわかったので、よかったかもしれません。
Dynnamic vs Static
Define-by-Run と Define-and-Runとも呼ばれます。それぞれを用いているフレームワークは上記と同じだったはずです。
Define-by-Run は実行時につながりが決まります。特に可変長の配列が入力される自然言語処理のようなケースを相性が良いです。しかしながら最適化が難しいようです。しかし、コンパイルができるようなフレームワークの機能が存在するようです。
Define-and-Run は実行前、コンパイル時?にすでにつながりが決まります。最適化はこちらの方が効きやすいようです。
FortLearnerでは前者の実装に多分なっているはずです。
Wengert Listでの実装
こちらで見つけた記述から実装しました。
FortLearnerで実装しているWengert-Listについてです。ただ、調べていると少し違う文献での記載と違うような気もしていますが、とりあえず私がやったものを書きます。
まず新しいtypeのvariable を用意します。これはGraph-Basedでも同様です。さらにこれらを格納するelementとさらにこれを格納するstack(おそらくこれがtapeに該当する)を用意しています。上記の論文でもあるように、例えば$z = x + y$という演算は、下記のように変換されます。
- z = x + y -> ["z", "add", ("x", "y")]
つまり、出力、処理内容、入力です。これらを適宜格納し、逆伝播ができるように情報(前のレイヤーのインデックスなど)を追加して、stack内に格納します。stackは複数用意されており、モデル定義時に自動で割り振られます。
最も美しくない点が、variableを用意する書きましたが、実装の都合上(~スキル、知識)、この中でした用いられないまた別の新しいvariableのtypeを定義してしまった点です。非常に見通しが悪く、拡張もしづらく感じています。最も修正したいと思っている点です。
Backward時には前のレイヤーの情報を取得することを再帰的に繰り返すだけがほとんどです。
Broadcast
これは常日頃からnumpyで楽をしていたなと感じたですが、Broadcastが非常に面倒でした。現在は自動的に(といっても行列、ベクトル、スカラーのみですが)形状を合わせるようにしているのですが、分岐がごちゃごちゃになってしまいました。とりあえず動いてはいますが、あまり検証を尽くせていないので、バグが大量に潜んでいる気がしてなりません。
いろいろ複雑で面倒な機能でしたが、まだまだレイヤー・Optimizerなど種類が足りないので、追加していきたいと思います。拡張性にも疑問があるので、できるだけ解消していきます。
以上