Minibatch Kmeans, Nested Minibatch Kmeans
今日はMinibatch Kmeansの解説です。通常のkmeansの解説ではアルゴリズムの詳細を変更せずに高速化する手法を紹介しましたが、今回はアルゴリズムを変更することで高速化します。短い記事になると思います。
Minibatch Kmeans
名前の通り、各イテレーションでは全サンプルでなくミニバッチを用いてクラスターの更新を行います。以下は論文中のアルゴリズムです。

各イテレーションでの全サンプルとクラスター間の行列積が必要なくなるため、速度的には非常に高速化されます。しかしながら、精度的にはkmeansと同じ結果になることがほとんどないようです。下図の緑が通常のkmeans、青がMinibatch Kmeansです。
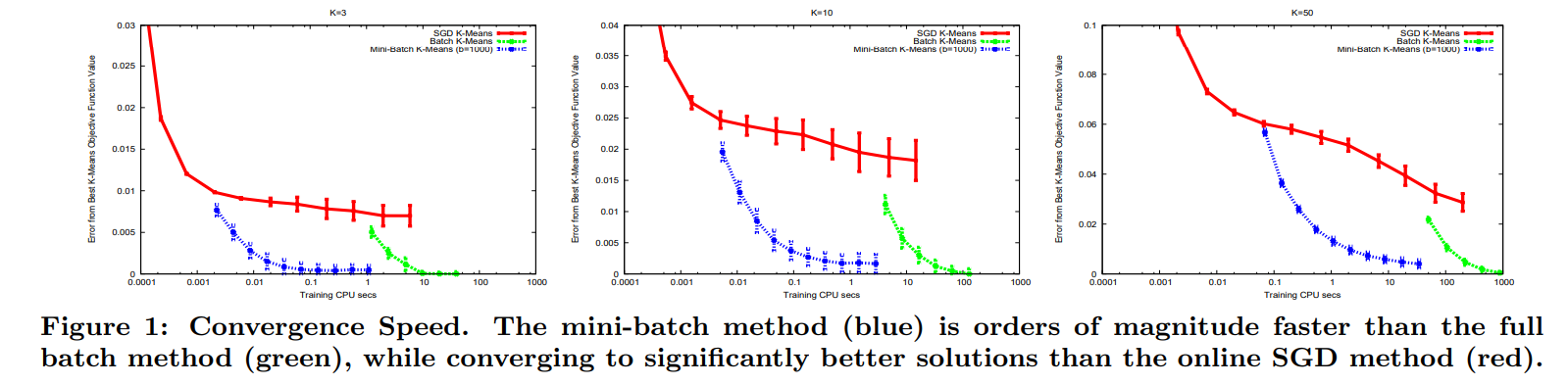
しかしながら、kmeansでそこまで精度を求めることに意味があるのかは疑問です。基本的にはクラスター結果を人が読み取ることが多いので、クラスター中心付近のサンプルがどのような属性であるかを判定できれば良いと思います。何らかの自動化システムに組み込む場合でも同様です。であれば少しの精度を犠牲にしても速度を求める方が良いと思っています。
Nested Minibatch Kmeans
次はNested Minibatch Kmeansです。
三角不等式による収束高速化
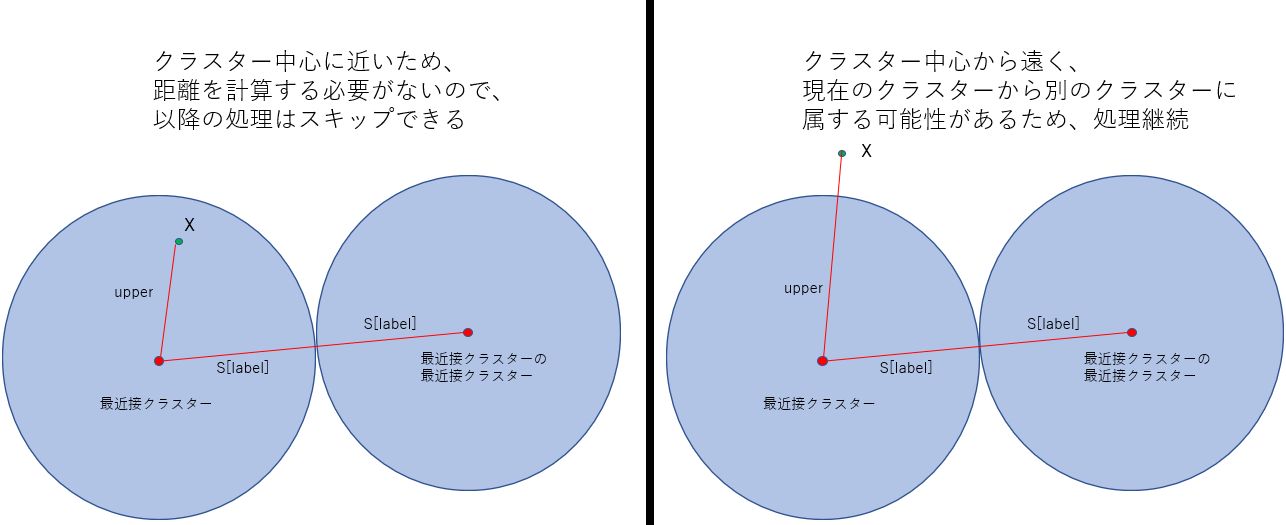
本当はKmeansの部分で説明するべきでしたが、三角不等式による収束高速化の方法について解説します。Elkanによって提案された手法で、大雑把に言ってしまうと、三角不等式を用いて計算する必要のないサンプルについての計算をスキップすることによって高速化を図ります。このアルゴリズムの説明にはの方法について説明します。完全には理解できていないのですが、scikit-learnのコードをみながら少しづつ確認していきました。
アルゴリズム
以下を定義しておきます。
\begin{eqnarray}
N&:& \text{サンプル$X$の数} \\
D&:& \text{特徴量の数} \\
K&:& \text{クラスターの数} \\
X&:& \text{$N$x$D$ 行列, サンプルのデータ} \\
C&:& \text{$K$x$D$ 行列, クラスターのデータ, $C_\text{old}$と$C_\text{new}$がある} \\
D&:& \text{$N$x$C$ 行列, サンプルとクラスター間の距離をすべて格納} \\
\end{eqnarray}
事前に計算、格納しておく値は以下です。
\begin{eqnarray}
I&:& \text{$K$x$K$行列, クラスター間の距離の半分} \\
S&:& \text{$K$個の要素を持つベクトル, 各クラスターの最近接クラスターまでの距離の半分} \\
U&:& \text{$N$個の要素を持つベクトル, 各サンプルの最近接クラスターまでの距離の上限。min(D, axis=1)で初期化される} \\
L&:& \text{$N$x$K$行列, 各サンプルの各クラスターまでの距離の下限。$D$を代入して初期化される} \\
\text{labels}&:& \text{$N$個の要素を持つベクトル, クラスターラベル} \\
\end{eqnarray}
# クラスターの初期化などは実施済み
# d(x, y) : xとyの間のユークリッド距離を計算
for n in range(N): # 全サンプルのループ
label = labels[n] # 現在のクラスターラベル
upper = U[n] # 上限距離を取得
r = True # 初回判定かどうか
# 上限距離が現在属するクラスターの作る球の外にある場合(下記図1参照)。
if S[label] < upper:
for j in range(K):
condition_1 = (j != label) # 現在の属するクラスター以外を探索
condition_2 = (upper > L[n, j]) # 上限が下限より大きい
condition_3 = (upper > I[j, label]) # クラスターが作る球の外にある(図1は最近接クラスターとその最近接クラスターに関してだが、ほぼ同様)
if (condition_1 & condition_2 & condition_3): # 最近接クラスターが更新される可能性があるため以下の処理を続行
if r: # 初回判定の場合
# このループの後でクラスター中心の更新を行うが、UとLは厳密な値で更新されるわけでなく、
# 保守的に更新されるため、ここで厳密な値が計算される(多分)
upper = d(X[n,:], C[label,:])
L[n,label] = upper
r = False
if ( (upper > L[x, j]) | (upper > I[j, label]) ): # 更新の必要が高い
# 上限が下限より大きいままか、クラスターjとクラスターlabel間の距離の半分以上の場合は更新の
# 可能性が高い。Lはここでしか更新されない。
d = d(x, j)
L[x, j] = d
if d < upper: # 上限よりdが小さいため、クラスターが更新される。upperも同様
label = j
upper = d
labels[n] = label
U[n] = upper
C_new = update_cluster_centers(X, C, labels) # 更新されたラベルを用いてクラスターを更新. 実際は新旧のラベルの更新分のみ
center_shift = compute_center_transition_distance_old_to_new(C_old, C_new) # セントロイドの遷移距離を計算
for n in range(N):
label = labels[n]
U[n] = U[n] + center_shift[label]
for j in range(K):
L[n,j] = max( L[n,j]-center_shift[j], 0 )
# 最初に戻る
この手法をさらに改善した手法についての記述はこちらのスライドを参照ください。
同じサンプルが複数回カウントされることの回避
Minibatch Kmeansのアルゴリズム11行目で分かるように同じサンプルの寄与はどんどん累積していきます。また、後続のイテレーションでクラスターが更新された際も、以前の寄与は異なる(~間違った)クラスターに残ったままとなってしまいます。特にこれはNested Minibatchを使うことで顕著になってしまうため、回避しなければなりません。そのため、Nested Minibatch Kmeansでは古い寄与は削除され、新しい寄与だけがカウントされます。
Nested Minibatch:ミニバッチのサンプルの選択方法の改良
Nested Minibatchについて。三角不等式を用いた高速化はそれまでのイテレーションで一度でも処理を行っていなければ意味がありませんが、ランダムなミニバッチサンプリングでは同じサンプルが続けて選ばれる確率は非常に低いです。そのためサンプリング方法を改良する必要があります。Nestedの名前の通り、t+1回目のイテレーションでは、t回目までのイテレーションで選択したサンプルのみをサンプリングの対象とします。つまり、1回目はサンプルAとB、2回目はAとBに加えCとDを、という風に進めていきます。しかしここでの問題点はtからt+1へ移る際にどれくらいのサンプルをミニバッチへ追加すればよいでしょうか。
この重要性を考えるために論文中ではまず二つの極端な場合を考えています。一つ目は全サンプルを投入する場合です。これは単純なKmeansになってしまうため意味がありません。二つ目は一つずつサンプルを追加する場合です。これではクラスターの更新がほとんど行われず計算の意味がなくなってしまいます。そのため、急速すぎず低速すぎずなミニバッチサイズの増加必要になります。
論文中では、サイズを増加させないか2倍にするかの場合について考えています。増加させない時にのクラスターの遷移距離$p$と、2倍にした際のクラスターの遷移距離$\sigma$を比較しています。前者が非常に大きい場合はバッチサイズの成長が小さすぎ、後者が非常に大きい場合はバッチサイズの影響が大きすぎます(論文中のFigure 1参照)。この二つの遷移距離の比率を見ることでどのように増加させていけばよいかがわかります。具体的には$\sigma/p > 100$の場合にはサンプルサイズ増加、以下の場合はサンプルサイズはそのままのようになります(100はハイパーパラメータです)。
以上