組合せ最適化を材料調達に応用してみた

はじめに

材料調達業務に数理最適化を使用した例があまり出てなさそうな気がしたので、新卒で調達業務をしていた頃に行った数年前の事例をデフォルメして記すことします。
大した例ではないですが、どなたかの役に立てば幸いです。

調達業務とは

• この記事ではメーカーの調達業務を取り扱うことにします。
• つまり自社の生産ラインに必要な材料を他社から買い付ける人（バイヤー）の業務を扱います。
• 例えばPCメーカーL社のバイヤーは半導体メーカーI社からCPUを買い付けます。

概要

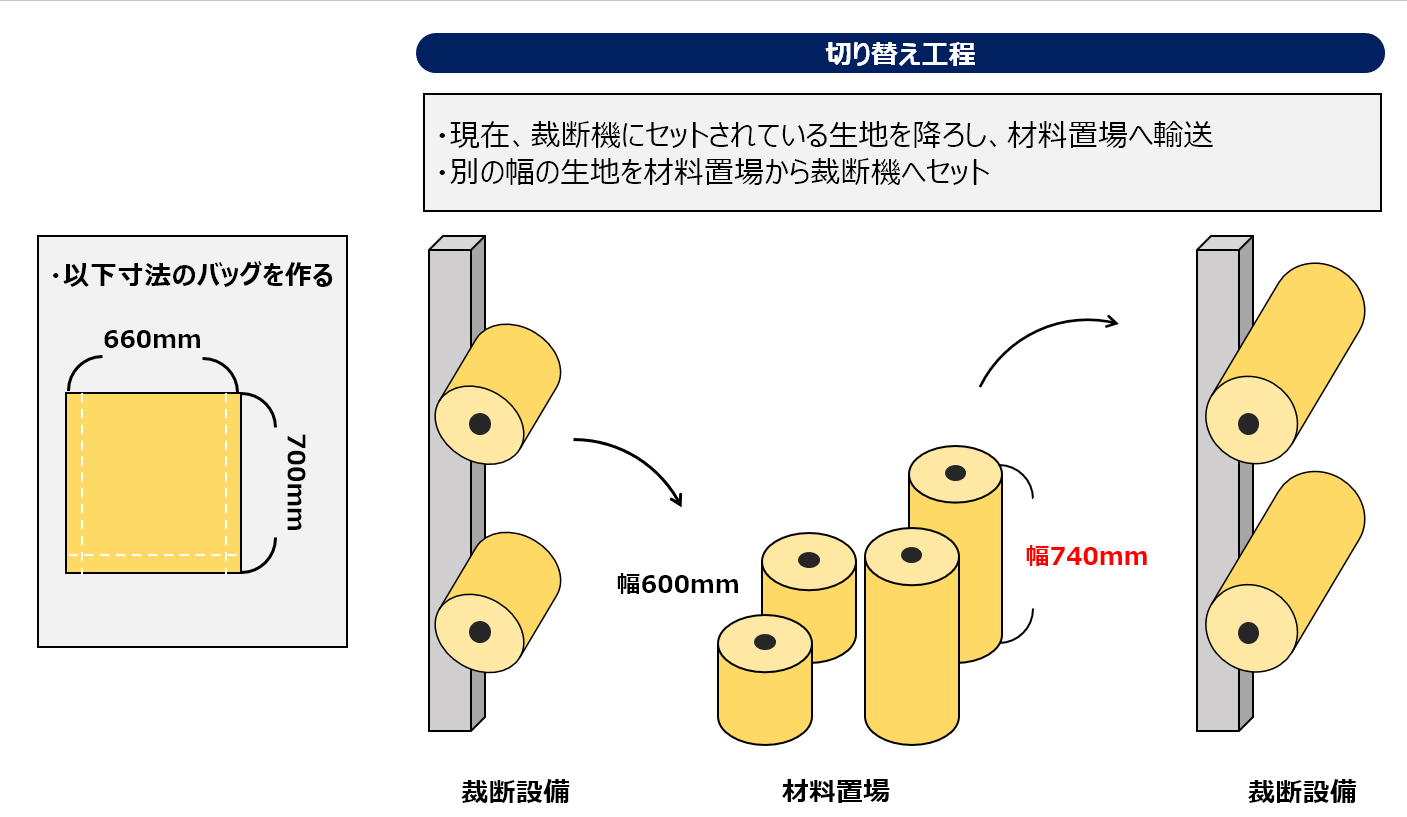
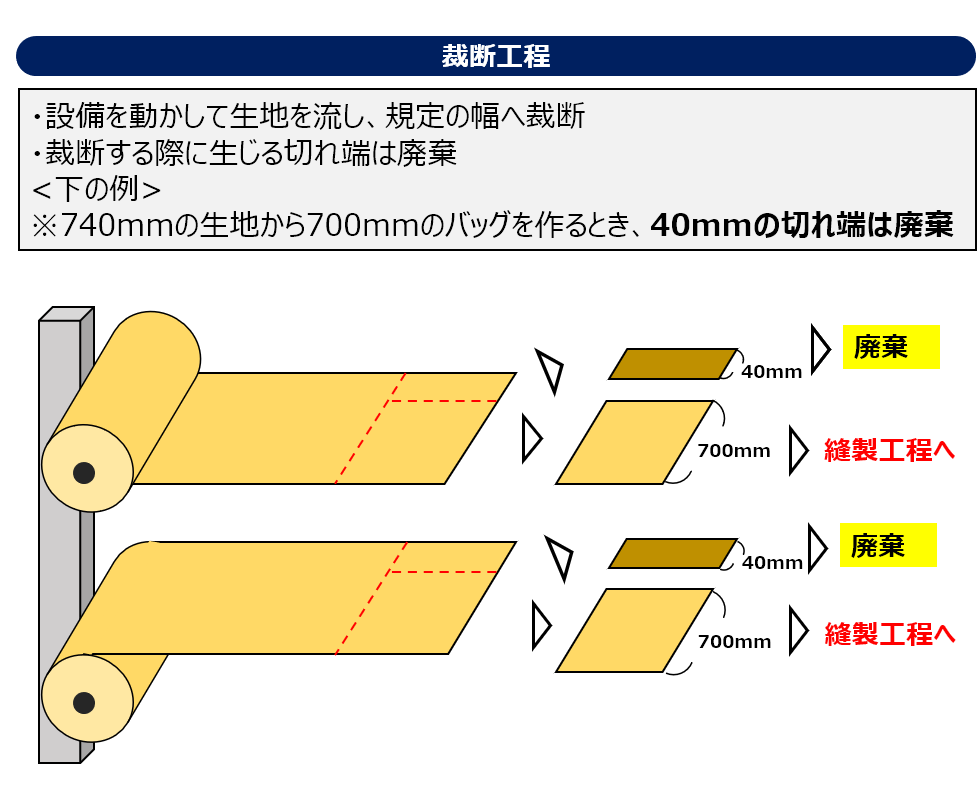
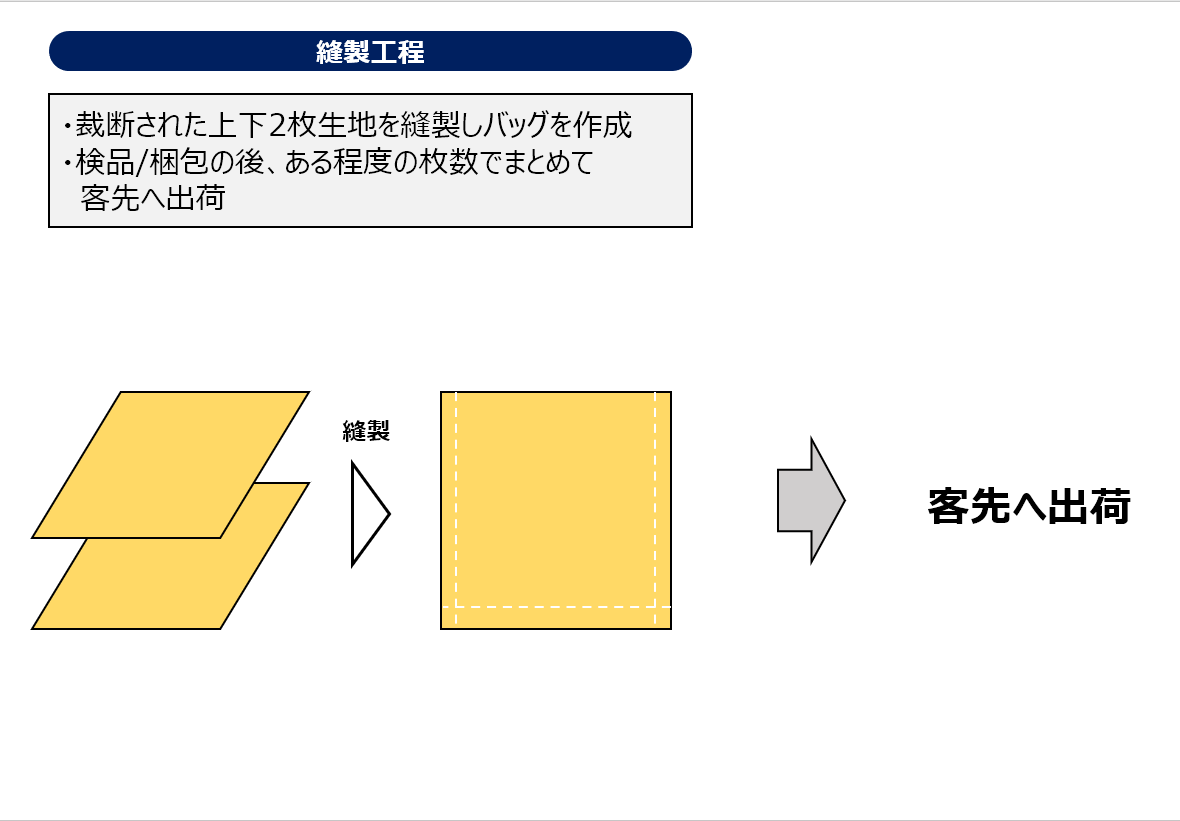
バッグ生産の工程

• C社の工場ラインでは様々な大きさのバッグ(同じ素材でサイズ違い)を作ることにする。
• バッグにはD社の生地を使用する。
• C社の工程は以下の通り。（詳細は下の図）
  • 切り替え工程：裁断機の上下から現在の生地を降ろし、別の幅の生地をセットする。
  • 裁断工程：裁断機を動かし、規定の幅へ裁断（トリミング）する。切れ端は廃棄する。
  • 縫製工程：裁断された上下の生地を縫い合わせバッグを作る。

※注意
実際は全く別の製品で最適化を行っています。
したがって上記製法は正しくないかもしれませんが、あくまで例としてお読みください。

###材料調達状況

• C社はD社から同じ素材の生地を5幅買っている。
• D社の生地は幅(mm)によらず、単価は100円/㎡とする。

No.	幅	単価(㎡)
1	520mm	100円/㎡
2	600mm	100円/㎡
3	740mm	100円/㎡
4	800mm	100円/㎡
5	1,000mm	100円/㎡

• 調達する生地の幅や幅数は変更できるが、D社の設備仕様上、生地の幅(mm)は10mm刻みで最小500mm～最大1,000mmしか作れない。

バッグの生産・販売状況

• ロール状の生地は重いので切り替え工程は大変。生地の幅数が1つ増えるごとに切り替え工程の工数が1,500,000円/年増える（ことにする）。
• 生地が5幅しかない一方、各販売先の要望サイズは多岐にわたるため、C社はこの5幅の生地から縦横サイズの異なる100種類のバッグを生産している。

考えたこと

• 裁断工程で生じる切れ端分の生地も100円/㎡で買っているので、バッグになることなく廃棄するのはもったいない。切れ裁断工程で生じる切れ端を最小にしたい。
• 一方で、生地の切り替え工数もなるべく抑えたい。

やりたいこと

• pythonを用いて切れ端となって廃棄する生地の金額と生地の切り替え工数が最も小さくなる生地幅の組み合わせを求めたい。

前提条件

• C社が客先に販売するバッグの寸法と年間数量は(ランダムで起こした)以下とする。

バッグの品番	幅寸法(mm)	縦寸法(mm)	数量(個/年)	生地幅(最適化前)
1	817	1,855	2,120	1,000
2	565	859	21,770	600
3	778	646	28,491	800
4	668	917	27,361	740
5	563	1,129	22,365	600
6	662	1,720	21,431	740
7	575	897	302	600
8	549	1,150	15,500	600
9	668	1,583	12,934	740
10	605	731	17,716	740
11	737	862	12,626	740
12	924	1,409	19,809	1,000
13	946	911	9,780	1,000
14	910	1,088	780	1,000
15	935	1,883	18,478	1,000
16	989	1,115	21,332	1,000
17	630	1,946	9,947	740
18	768	619	23,197	800
19	585	1,576	26,454	600
20	958	1,121	10,220	1,000
21	564	266	10,511	600
22	665	281	16,989	740
23	941	1,775	10,050	1,000
24	546	1,092	8,674	600
25	840	1,962	408	1,000
26	932	1,650	894	1,000
27	596	1,440	23,985	600
28	649	1,861	6,140	740
29	936	631	20,634	1,000
30	915	994	13,803	1,000
31	865	324	15,460	1,000
32	971	586	6,415	1,000
33	722	1,003	3,979	740
34	933	1,681	22,587	1,000
35	846	1,991	10,813	1,000
36	740	1,439	8,708	740
37	586	940	7,609	600
38	843	622	1,952	1,000
39	904	1,261	15,705	1,000
40	523	1,366	12,390	600
41	508	424	18,736	520
42	659	1,945	18,830	740
43	978	1,408	14,805	1,000
44	987	314	24,601	1,000
45	661	750	8,738	740
46	947	728	16,274	1,000
47	832	269	19,437	1,000
48	707	575	23,943	740
49	982	1,775	3,118	1,000
50	576	236	24,583	600
51	899	788	832	1,000
52	845	243	13,364	1,000
53	866	468	25,456	1,000
54	960	1,413	15,472	1,000
55	960	1,535	12,313	1,000
56	536	904	28,872	600
57	988	1,745	9,226	1,000
58	894	703	5,418	1,000
59	509	1,006	17,315	520
60	623	1,601	28,039	740
61	985	744	3,017	1,000
62	656	1,797	6,931	740
63	780	361	24,886	800
64	606	313	26,229	740
65	820	794	21,857	1,000
66	911	627	24,301	1,000
67	935	937	6,146	1,000
68	656	691	17,998	740
69	586	1,081	6,946	600
70	506	1,265	14,622	520
71	732	271	26,999	740
72	773	507	5,041	800
73	547	1,435	18,547	600
74	870	1,874	25,541	1,000
75	599	906	9,180	600
76	769	706	6,036	800
77	592	397	15,923	600
78	595	1,231	11,845	600
79	831	1,747	4,402	1,000
80	685	1,933	29,523	740
81	549	1,342	20,865	600
82	618	464	11,997	740
83	722	939	7,863	740
84	802	523	16,194	1,000
85	554	1,516	22,599	600
86	506	1,488	14,829	520
87	856	574	22,849	1,000
88	764	1,629	7,477	800
89	529	1,674	1,061	600
90	589	733	14,085	600
91	759	883	2,513	800
92	719	474	4,763	740
93	508	1,961	23,064	520
94	747	587	20,981	800
95	864	1,646	316	1,000
96	576	536	25,852	600
97	764	289	18,777	800
98	598	1,203	7,705	600
99	708	925	4,784	740
100	800	969	4,193	800

• バッグの縦方向と幅方向を置換して裁断することはできない。
• 今回は在庫については検討から除外する。

pythonで作ってみた

• 前回のきれいでないコードを用いているので、読みにくいですがご容赦ください。

ライブラリのインストール

python

import math
import numpy as np
import pandas as pd
from pulp import*
from ortoolpy import addvars, addbinvars

生産するバッグの品番情報(CSV)の読み込み

• CSVを読み込み、品番数×生地幅(D社生産可能な500mm～1000mm：10mm刻み)の表へ変形。
• この後の計算の都合上、tbl2のTrue/Falseを入れ替え(tbl_2)。

python

tbl1 = pd.read_csv('bag_model.csv') #csvの読み込み

a = tbl1['幅寸法(mm)']
b = tbl1['縦寸法(mm)']
c = tbl1['数量(個/年)']
widmin = 500 # 生地の最小幅は500mm
widmax = 1000  # 生地の最大幅は1000mm
widlist =[i for i in range(widmin,widmax+1,10)] 
# D社の作れる生地の幅をリスト化（10mm刻みで作れる。）

bag = len(tbl1) #bagのモデル数
widnum=len(widlist)
tbl2 = np.zeros(bag*widnum).reshape(bag,widnum)
for i in range(bag):
    just = math.ceil(a[i]/10)*10 #バッグを作成できる最小の生地幅。
    startrow = (just-500)//10
    tbl2[i,startrow:]=1 # バッグを作成できる最小幅(mm)から最大幅1000mmまで1にする。
tbl2 = tbl2.astype(np.bool).copy() #作成可能な生地幅を1に変更。

tbl_2 = ~tbl2 #~でFalseとTrueを裏返す。このあとtbl4で使用する。
tbl_2 = tbl_2.astype(np.int) # 0と1に戻す。

品番ごとの総切れ端(㎡/年間)表の作成

• 各品番ごとですべての生地幅における総切れ端(㎡/年間)を計算しテーブルを作成。
  • (生地幅－バッグ横幅)×バッグ縦幅×年間数量で計算可能。
• 生地幅<バッグ横幅の場合は生産できないので、便宜的に(最適解にならないよう)1億㎡とした。
  
  ※前回のコードを流用しているのでtbl3はありません。

python

#各幅での切れ端(m2/年)の表を作成。
#生地幅<バッグの幅になってはならないので、ペナルティで1億m2。
tbl4 = tbl_2*100000000
for i in range(bag):
    just = math.ceil(a[i]/10)*10
    startrow = (just-500)//10 #最小の幅が何列目か計算。
    count = 0 
    for j in range(widnum-startrow):
        material_loss =((just - a[i] + count)/1000)*(b[i]/1000)*2*c[i] #切れ端m2/年の計算。(生地幅ーバッグ横幅)×バッグ縦幅×年間数量
        tbl4[i,j+startrow]=material_loss
        count+=10

変数の宣言

• 生地幅の採用有無が入るバッグ数×生地幅数のバイナリ変数を作る(tbl5)。
• 採用幅数を計算するためのバイナリ変数を作る(tbl6)。

python

tbl5 = np.array(addbinvars(widnum,bag))
#バッグの品番数×生地の幅数で変数matrixを作成(バイナリ変数)

tbl6 = addbinvars(widnum) #生地の幅数計算のためのテーブル。使用する生地幅に1が立つのでlpSumで幅数を計算可能。

tbl_2 = tbl_2.T.tolist() #目的関数作成用に変換
tbl4 = tbl4.T.tolist()

モデル化・最適化処理

• 条件を式に落とし最適化計算。

python

Closs = 100 #切れ端金額のペナルティ 100円/m2。
Cswt = 1500000 #切り替え工数金額のペナルティ。150万円/幅数。

m = LpProblem(sense=LpMinimize) #最小化問題の宣言
m += (Closs * lpDot(tbl4,tbl5)
    + Cswt * lpSum(tbl6))
# 目的関数の式
# 1行目はすべてのバッグ品番の切れ端廃棄金額(年間)
# 2行目は切り替え工数(年間)
# すべての合計が最小になるときの各バッグ品番ごとの生地幅表を出力

for i in range(widnum):
    m += tbl6[i] >= (lpSum(tbl5[i,:])/bag)

# 制約条件の式1
# 選択された生地幅に1を、選択されない生地幅に0が立つ。

for j in range(bag):
    m += lpSum(tbl5[:,j]) <= 1
    m += lpSum(tbl5[:,j]) >= 1

# 制約条件の式2
# 1品番あたり、必ず1つ幅を決める

m.solve()
print('目的関数', value(m.objective))

結果の出力

• 計算結果をCSVに出力。
• 最初に読み込んだbag_list.csvの右に最適化の結果を追記して、新たにbag_opt.csvとして保存。

python

result = np.vectorize(value)(tbl5).astype(int).T #ソルバーの出力結果（生地幅数×品番数で0-1が埋まっている）
widkey = [i for i in range(widnum)] 
widdic = {key: width for key, width in zip(widkey, widlist)} 
result = [widdic[sum(result[i]*widkey)] for i in range(bag)] #各品番の最適幅のリストを作衛

tbl1['幅寸法(mm)'] = a.copy()
tbl1['縦寸法(mm)'] = b.copy()
tbl1['数量(個/年)'] = c.copy()
tbl1['最適幅']= result
tbl1.to_csv('bag_opt.csv',index=False,encoding='utf-8_sig')  #csvで出力。

バッグの品番	幅寸法(mm)	縦寸法(mm)	数量(個/年)	生地幅(最適化前)	生地幅(最適化後)
1	817	1,855	2,120	1,000	870
2	565	859	21,770	600	600
3	778	646	28,491	800	780
4	668	917	27,361	740	670
5	563	1,129	22,365	600	600
6	662	1,720	21,431	740	670
7	575	897	302	600	600
8	549	1,150	15,500	600	550
9	668	1,583	12,934	740	670
10	605	731	17,716	740	670
11	737	862	12,626	740	780
12	924	1,409	19,809	1,000	940
13	946	911	9,780	1,000	990
14	910	1,088	780	1,000	940
15	935	1,883	18,478	1,000	940
16	989	1,115	21,332	1,000	990
17	630	1,946	9,947	740	670
18	768	619	23,197	800	780
19	585	1,576	26,454	600	600
20	958	1,121	10,220	1,000	990
21	564	266	10,511	600	600
22	665	281	16,989	740	670
23	941	1,775	10,050	1,000	990
24	546	1,092	8,674	600	550
25	840	1,962	408	1,000	870
26	932	1,650	894	1,000	940
27	596	1,440	23,985	600	600
28	649	1,861	6,140	740	670
29	936	631	20,634	1,000	940
30	915	994	13,803	1,000	940
31	865	324	15,460	1,000	870
32	971	586	6,415	1,000	990
33	722	1,003	3,979	740	780
34	933	1,681	22,587	1,000	940
35	846	1,991	10,813	1,000	870
36	740	1,439	8,708	740	780
37	586	940	7,609	600	600
38	843	622	1,952	1,000	870
39	904	1,261	15,705	1,000	940
40	523	1,366	12,390	600	550
41	508	424	18,736	520	550
42	659	1,945	18,830	740	670
43	978	1,408	14,805	1,000	990
44	987	314	24,601	1,000	990
45	661	750	8,738	740	670
46	947	728	16,274	1,000	990
47	832	269	19,437	1,000	870
48	707	575	23,943	740	780
49	982	1,775	3,118	1,000	990
50	576	236	24,583	600	600
51	899	788	832	1,000	940
52	845	243	13,364	1,000	870
53	866	468	25,456	1,000	870
54	960	1,413	15,472	1,000	990
55	960	1,535	12,313	1,000	990
56	536	904	28,872	600	550
57	988	1,745	9,226	1,000	990
58	894	703	5,418	1,000	940
59	509	1,006	17,315	520	550
60	623	1,601	28,039	740	670
61	985	744	3,017	1,000	990
62	656	1,797	6,931	740	670
63	780	361	24,886	800	780
64	606	313	26,229	740	670
65	820	794	21,857	1,000	870
66	911	627	24,301	1,000	940
67	935	937	6,146	1,000	940
68	656	691	17,998	740	670
69	586	1,081	6,946	600	600
70	506	1,265	14,622	520	550
71	732	271	26,999	740	780
72	773	507	5,041	800	780
73	547	1,435	18,547	600	550
74	870	1,874	25,541	1,000	870
75	599	906	9,180	600	600
76	769	706	6,036	800	780
77	592	397	15,923	600	600
78	595	1,231	11,845	600	600
79	831	1,747	4,402	1,000	870
80	685	1,933	29,523	740	780
81	549	1,342	20,865	600	550
82	618	464	11,997	740	670
83	722	939	7,863	740	780
84	802	523	16,194	1,000	870
85	554	1,516	22,599	600	600
86	506	1,488	14,829	520	550
87	856	574	22,849	1,000	870
88	764	1,629	7,477	800	780
89	529	1,674	1,061	600	550
90	589	733	14,085	600	600
91	759	883	2,513	800	780
92	719	474	4,763	740	780
93	508	1,961	23,064	520	550
94	747	587	20,981	800	780
95	864	1,646	316	1,000	870
96	576	536	25,852	600	600
97	764	289	18,777	800	780
98	598	1,203	7,705	600	600
99	708	925	4,784	740	780
100	800	969	4,193	800	870

結果と効果整理

• 最適化前は5幅、最適化後は7幅となった。

No.	幅(最適化前)	幅(最適化後)
1	520mm	550mm
2	600mm	600mm
3	740mm	670mm
4	800mm	780mm
5	1,000mm	870mm
6	-	940mm
7	-	990mm

• 最適化による効果は△6,803千円/年となった。詳細は以下の通り。

項目	最適化前	最適化後	効果
1.切れ端生地の金額	17,099,145円/年	7,295,875円/年	△9,803,270円/年
2.切り替え工程の工数	7,500,000円/年	10,500,000円/年	+3,000,000円/年
1と2の合計	24,599,145円/年	17,795,875円/年	△6,803,270円/年

まとめ・感想

　実際の業務でも大幅な効果が出ました。何より一度このような計算の仕組みを作ってしまえば、販売数量・材料市況などが変化しても常に最適解で材料発注ができることが大きいと思います。
　今回の事例では材料調達先における生産ラインの制約を守ったうえで発注戦略を検討し、自社の工場ラインの無駄取りを行いました。このようにメーカーの調達というのは材料調達先の生産条件に精通し、調達先の潜在能力を最大限活用しながら、自社のものづくりを改善していくことができる役職であると思います。
　いずれにしても、最適化を用いて材料調達先と自社製造現場というサプライチェーンをまたいだ無駄取りが簡単にできるのは素晴らしいことだと思います。このような活動も広まっていけばよいなと思う次第です。

参考

• 「組合せ最適化でナーススケジューリング問題を解く」
• 「遺伝的アルゴリズムでナーススケジューリング問題（シフト最適化）を解く」