はじめに
フィボナッチ数を求めるコードを書く問題に挑戦していたところ再帰関数が出てきて頭がパンクしそうだったので整理するためにも記事にしてみます。
メインは再帰関数ですがついでにフィボナッチ数とメモ化に関しても説明してあるのでよければ見ていってください。
フィボナッチ数列とは
本題ではないので詳しい説明は割愛しますが 0, 1 もしくは 1, 1 から始まり、前2つ前の数字を足し合わせると次の数になる数列のことです。

こんな感じ。
漸化式
「うわ何や難しい文字出てきたわ戻ろ」
と思って帰りかけた文系のあなた、もうちょっとお付き合いください。
ガチガチ文系の筆者ですがなんとか理解して噛み砕いてみたので大丈夫です。多分。
前項目の画像では21で数列が終わっていますが、その次の数字は何になるでしょうか?
数列を構成する各々の数を数列の「項」といいますが、この項に番号をふってみましょう。配列番号を付けるイメージです。

21の次、つまり9番目の数字を求めたいわけです。
”前2つの数字を足し合わせると次の数になる”という性質を考えると7番目+8番目なので
13+21=34 となります。
数列にふった”番号”に注目して式を作り替えるとどうなるでしょうか。
7番目+8番目=9番目 ですね。
上の式をもう少しいじってみます。7番は9番の2つ前、8番は9番の1つ前なので
(9ー2番目)+(9ー1番目)=9番目 ですよね。
ポイントは3つ
- 0番目の数字は0
- 1番目の数字は1
- 2番目以降は前2つ前の数字を足し合わせると次の数になる
では、フィボナッチ数列(F)のn番目の数を求めるには?
\large{F_{0} = 0,}\\
\large{F_{1} = 1,}\\
\large{F_{n} = F_{n-2} + F_{n-1}} \small{(n ≥ 2)}
このように数列の項同士の関係性を利用して作られた式を漸化式と呼ぶそうです。
この漸化式は再帰的な定義になっているので再帰呼び出しを使って簡単にプログラムを書くことができます。
再帰関数
再帰関数とは何かを説明する前にまずは上記の漸化式を利用してどの様なプログラムがかけるのかをみていきます。
def fibonacci(n)
return n if n == 0 || n == 1
fibonacci(n - 2) + fibonacci(n - 1)
end
上でも書いた様に0番目の数=0、1番目の数=1なのでこの2択に当てはまる場合はreturnでnを返します。
それ以降は漸化式と同じ要領でプログラムを書いてあげればOKです。
fibonacciという関数内にまたfibonacci関数が存在しているわけですが、この様な自分自身を呼び出す関数を再帰関数といいます。
処理の流れ
では処理の流れはどうなっているのでしょうか。
再帰呼び出しは
関数内にある自分自身の中に入って処理→さらにその中の自分自身の中に入って処理…
という風にreturnに引っかかるまでループを繰り返します。
例えば n = 6 とした時、2行目は条件不一致によりスキップされ3行目へ進みます。
3行目では fibonacci(4) + fibonacci(5) となり、 fibonacci(4) の処理が始まるのです。
文章だと分かりづらいので図にしてみましょう。
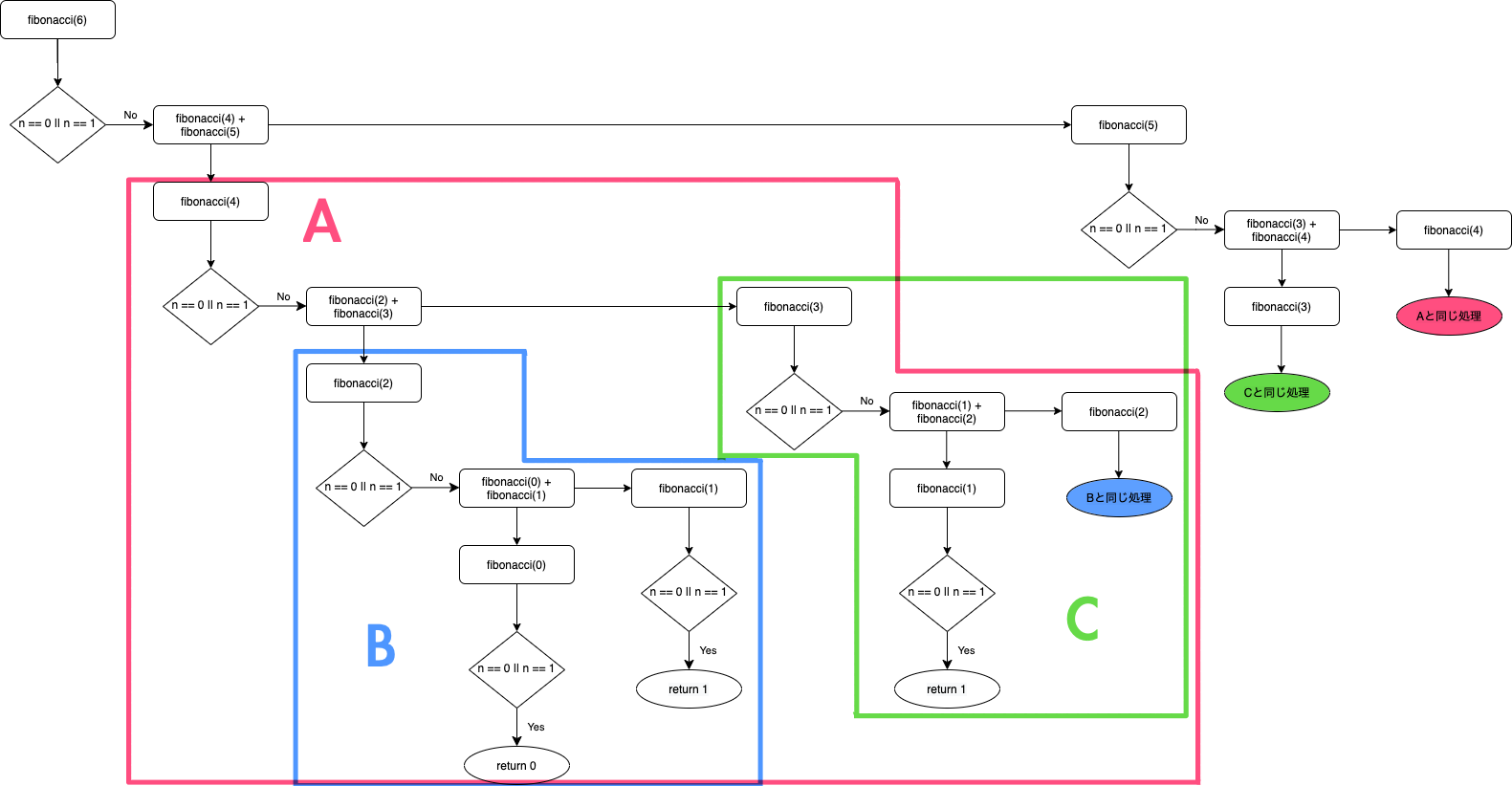
こんな感じでreturnに行き当たるまでループします。
ループの戻り値である0か1を順番に足していくことで最終的にn番目の数を求めるようになっているわけですね。
再帰関数の弱点
お気づきの方もいらっしゃるかと思いますが、シンプルに書ける便利な再帰呼び出しにも弱点があります。
それは同じ項を何度も重複して計算してしまうことです!
上記の様な6番目程度の数を求める場合は大したループではないのですが、100番目の数を求めるとなると、同じ計算を何度も繰り返してしまうために処理が終わるまでに長い時間がかかってしまうのです。
この欠点を補うのがメモ化です。
メモ化
上の図を見てもらうとA, B, Cと全く同じ処理が再び行われている部分がありますよね。
そこで文字通り一度計算した内容をメモ(キャッシュ)しておき2回目以降はメモをチラ見するだけで済むのがメモ化です。
メモ化を利用して書き直したプログラムがこちら
def fibonacci(n)
@memo ||= []
return n if n == 0 || n == 1
@memo[n] ||= fibonacci(n - 2) + fibonacci(n - 1)
end
||=は「||」演算子の自己代入演算子です。
左辺が 偽 か 未定義 なら左辺に右辺を代入する、という意味になります。
2行目でmemoというメモ帳を用意してあげて、4行目で未だ計算したことのない値の場合はメモしておく流れになっています。
これで100番目の数字でも一瞬で求めることができるようになりました。お疲れ様でした!
おわりに
ここまでご覧いただいてありがとうございました。
フィボナッチ数の求め方は他にもあるようなので色々試してみたいと思います。