ディープラーニング基礎理論_順伝播編

当記事では、ディープラーニングを実現するための基本的なアルゴリズムである「ニューラルネットワーク」における「順伝播計算」の基礎的な理論を、文章・数式・図・実装コードを用いて説明していきます。
「逆伝播計算」・その他ディープラーニングにおける手法（「重みの最適化手法」「各種正規化手法」など）については、今後別記事で投稿する予定です。
記事の内容について誤り等がありましたら、ご指摘いただけますと幸いです。

全体の流れ

ディープラーニングとは、ディープニューラルネットワークを用いた機械学習手法です。
ディープニューラルネットワークとは、機械学習手法の1つであるニューラルネットワークを多層化したものであり、アルゴリズム自体はニューラルネットワークと同じです。
また、ニューラルネットワークとは、パーセプトロンを重ねたものです。
そのため、以降の説明では「パーセプトロン」 → 「ニューラルネットワーク」の流れで説することで、ディープラーニングのアルゴリズムを説明していきます。

（ニューラルネットワークの層を深くする（ディープにする）ことで、ディープニューラルネットワークと呼ばれるようになりますが、何層目からディープといえるかについての定義はなく、ニューラルネットワークと、ディープニューラルネットワークの明確な境界は存在しません。）

また記事の最後には、ニューラルネットワーク全体のサンプルコード（順伝播部分のみ）を載せていますので、ご参考にしてください。

当記事で扱う領域

ディープラーニングでは、モデル（ディープニューラルネットワーク）を学習させる「学習時」と、学習させたモデルを使い、何らかの推論を行う「推論時」の2段階に分かれます。
（「推論時」の計算は、「学習時」の計算の一部のため、「学習時」の計算のみを説明していきます。）
そして「学習時」におけるモデルの計算は、以下3段階で構成されます。
当記事では1つ目の「順伝播計算」、2つ目の「誤差の計算」に焦点を置いて説明していきます。
（「推論時」の計算は、1つ目の「順伝播計算」のみです）

1. 順伝播計算
入力層から入ってきた入力値に対し、計算処理を行いながら、後続の層に値を伝えていく（入力層 → 出力層に向かって値を順方向に伝播させていく）。

2. 誤差の計算
出力層で、順伝播計算による最終的な値を出力し、正解値との誤差を算出する。

3. 逆伝播計算
出力層で算出した誤差を、入力層へ向かって逆方向に伝えながら（出力層 → 入力層へ向かって値を逆伝播させながら）、モデルのパラメータ（重み・バイアスなど）の値を更新していく。

パーセプトロン

ニューラルネットワークとは、多層パーセプトロン（パーセプトロンを多層にしたもの）とほぼ同義のため、まずパーセプトロンの説明から入ります。

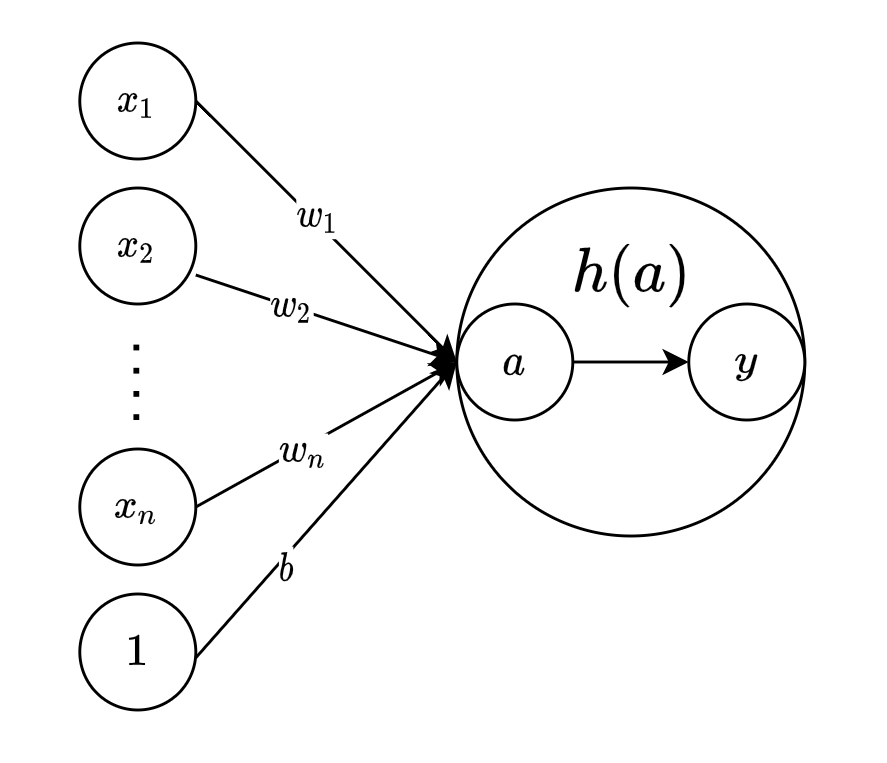
パーセプトロンとは、複数の信号を受け取り、1つの信号を出力するアルゴリズムのことです。
出力される結果は、信号を流す($1$)か、流さない($0$)の2値です。
具体的には、各入力値に対し、対応する重みをかけ、バイアスを足したものを、ステップ関数という活性化関数に通し、その結果（$0$ or $1$）を出力します。

　　　　　　　　

y = h(b + \sum_{i=1}^{N}x_iw_i)

$x_i$ : 入力値
$w_i$ : 重み
$b$ : バイアス
$h(a)$ : 活性化関数
$y$ : 出力

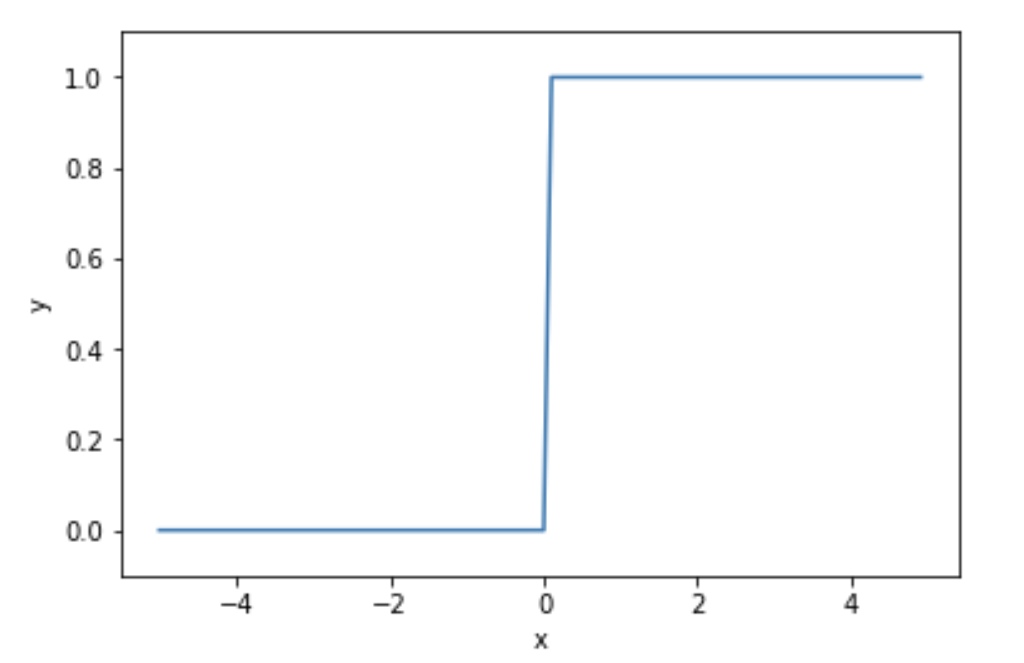
ステップ関数とは、入力が$0$以下のとき$0$を出力し、入力が$0$を超えたとき$1$を出力する関数です。
言い換えると、$0$を閾値とし、入力値が閾値を超えたら$1$、超えなければ$0$を出力する関数と言えます。

y = \left\{
\begin{array}{ll}
0 & (a \leq 0) \\
1 & (a > 0)
\end{array}
\right.

ステップ関数

# numpyを用いて、以下2段階の手順で、行列として渡されるxを、一度に0,1に変換する
# まず、行列の全要素について、x>0の要素はtrueに、x<=0の要素はfalseに、一度に変換する（yは、各要素がboolean型（true,false）の行列になる）
# 次に、yの全要素(boolean型)を、一度にint型に変換する（trueの要素は1に、falseの要素は0になる）
def step(x):
    y = x > 0
    return y.astype(np.int)

　　　　　　　　　　　　　

つまりパーセプトロンとは、何らかの入力値を受け取り、その入力値を基にした計算結果の値が、0以下なら0を出力し、0を超えたら1を出力する、ネットワークモデルのことをいいます。

ニューラルネットワーク

次に、ニューラルネットワークの説明に入ります。

ニューラルネットワークとは、パーセプトロンを多層に重ねたネットワークモデルのことです。

あくまでもパーセプトロンを複数重ねたものであるため、ニューラルネットワークも、「各入力値に対し、対応する重みをかけ、バイアスを足したものを、活性化関数に通して何らかの値を出力する」という基本的なアルゴリズム自体は、先ほど説明したパーセプトロンと同じです。

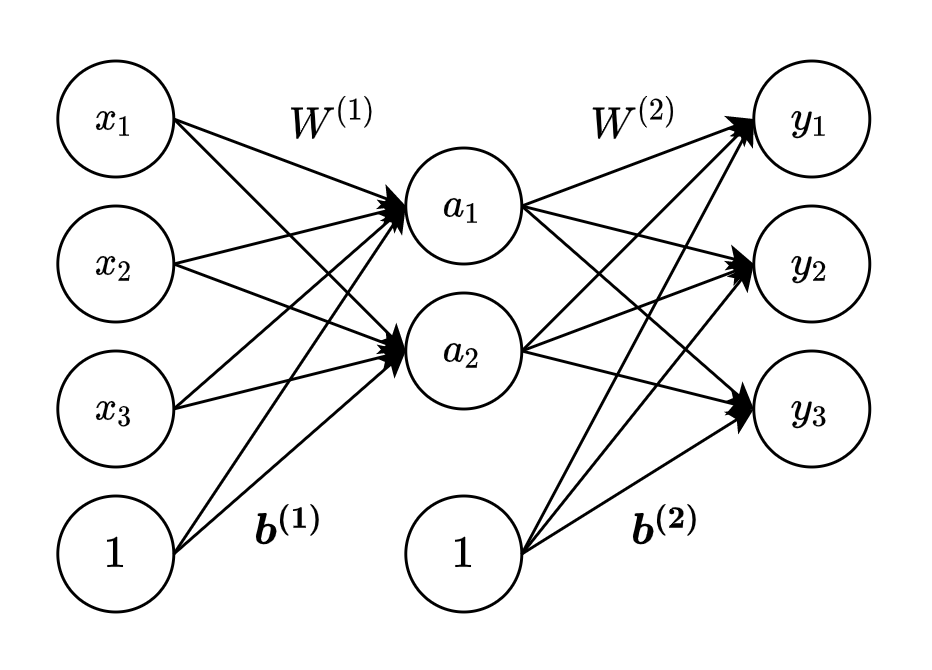
パーセプトロンとの違いは、「入力層と出力層の間に、中間層（隠れ層）を持つ」「使用される活性化関数がステップ関数以外」という2点だけです。

「入力層と出力層の間に、中間層（隠れ層）を持つ」という点については、入力層から入ってきた入力値に対し中間層で計算を行い、その計算結果を次の中間層（中間層が1層の場合は出力層）に伝えます。
層の数え方としては、ノード間のエッジ（線）の縦のまとまりを1層分とします。そのため以下図は、2層のニューラルネットワークといえます。

　　　　　　　　

出力層の $y1$, $y2$, $y3$ の値はそれぞれ以下のように計算されます。

a_1 = h\,(\,x_1 w^{(1)}_{11} + x_2 w^{(1)}_{12} + x_3 w^{(1)}_{13} + b^{(1)}_1\,)\\
a_2 = h\,(\,x_1 w^{(1)}_{21} + x_2 w^{(1)}_{22} + x_3 w^{(1)}_{23} + b^{(1)}_2\,)\\

y_1 = a_1 w^{(2)}_{11} + a_2 w^{(2)}_{12} + b^{(2)}_1\\
y_2 = a_1 w^{(2)}_{21} + a_2 w^{(2)}_{22} + b^{(2)}_2\\
y_3 = a_1 w^{(2)}_{31} + a_2 w^{(2)}_{32} + b^{(2)}_3\\

重みの表記についてですが、
上付き文字は、層の番目を、
下付き文字は、左が次層のノード番目、右が前層のノード番目を、表します。

W^{(1)}_{21}

例えば、上記表記は「第1層目の、次層（第2層）の2番目のノードと前層（第1層）の1番目のノードの間の重み」を表しています。

上記計算式を、入力値・重み・バイアスを行列表記で一般化して表すと、以下になります。
（上記計算式の場合、入力値・バイアスはベクトルのため、正確な表記はそれぞれ $\boldsymbol{x}$、$\boldsymbol{b}$ですが、表記を統一させるために、行列で表現しています。）

A = h\,(\,XW^{(1)}+B\,)\\
Y = AW^{(2)} + B

活性化関数

活性化関数とは、入力に対応する出力が非線形になるように変換するための関数です。

そもそもニューラルネットワークの層を深くすることのモチベーションは、「ネットワーク全体の表現能力を向上させる（より複雑な計算を行い、結果的により複雑な問題を解くことができるモデルを作り出す）」ことにあります。

一方、中間層の活性化関数に、（入力を定数倍するだけである）線形関数を用いると、結果的に層を深くする意味がなくなってしまいます。

なぜなら、中間層を重ね、入力を何回定数倍していったとしても、それは結果的に一回定数倍することと同じになるためです。

書籍「ゼロから作るDeep-Learning-―Pythonで学ぶディープラーニングの理論と実装」で記載されている以下数式表現がわかりやすいです。

h(x)=cx\\
y(x)=h(h(h(x)))=c \times c \times c\times x = c^3 x\\
y(x)=ax \,(a=c^3)\\

$y(x)=h(h(h(x)))$は、3層のネットワークを表現しており（$h(x)$は、線形な活性化関数）、
これは中間層を持たない（活性化関数を用いない）ネットワーク$y(x)=ax$と同じことになります。

つまり、中間層の活性化関数に線形関数を用いた場合、どれだけ深い層を持たせたネットワークであっても、中間層を持たないネットワークで表現できてしまう、ということです。

活性化関数には様々な種類が存在しますが、中間層で用いられる（非線形な）活性化関数として、「シグモイド関数」「ReLU」の2点だけ挙げます。

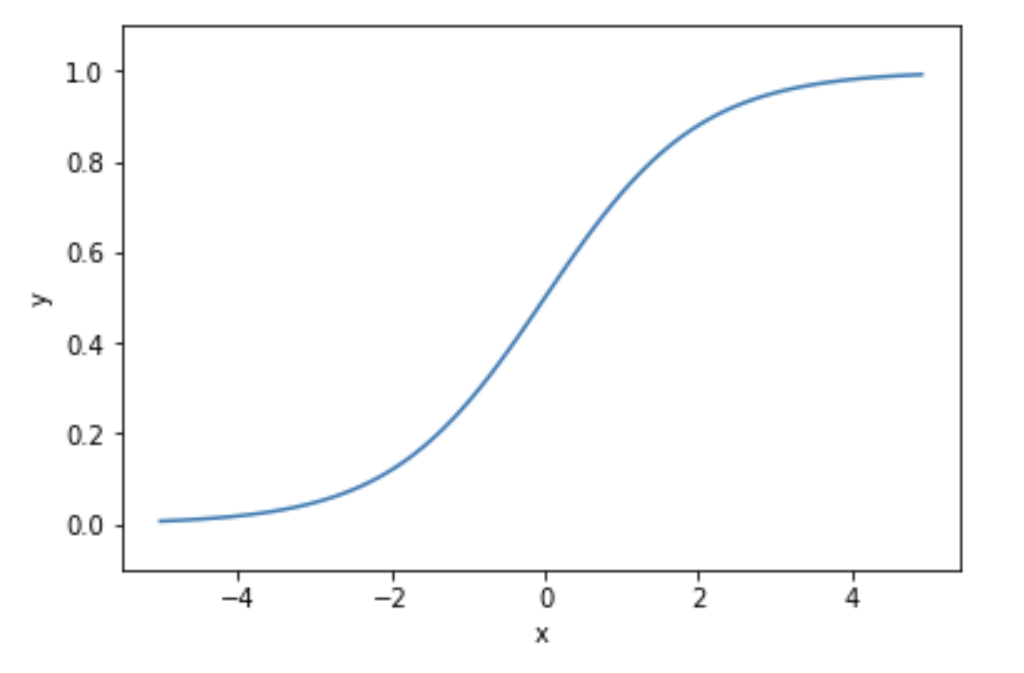
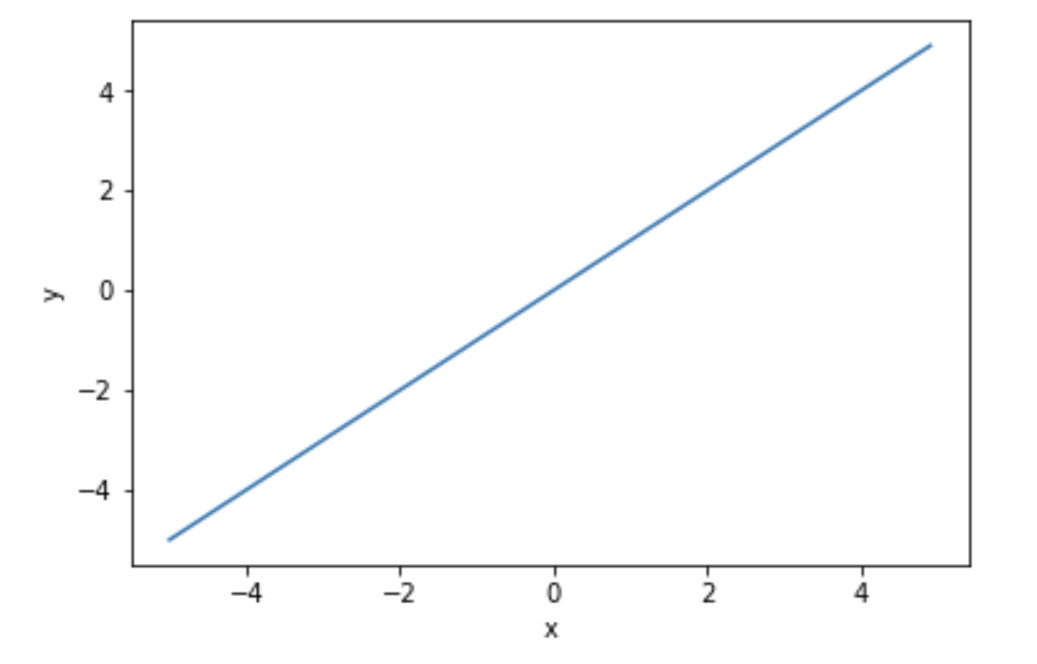
シグモイド関数

入力に対し、$0$-$1$間の連続的な実数値を出力します。
グラフとしては、以下のように滑らかな曲線を描きます。

y = \frac{1}{1+exp(-x)}

シグモイド関数

# ニューラルネットワークでは、引数xは行列になります。
# そのため、numpyのexp()を使用し、行列の全要素に対してeの-x乗を行う必要があります。
def sigmoid(x):
    y = 1 / (1 + np.exp(-x)) 
    return y

　　　　　　　　　　　　　

ですが、中間層の活性化関数にシグモイド関数を設定すると、「逆伝播計算時」に、勾配消失を引き起こし、モデルの学習（パラメータの更新）が上手くいかなくなるため、現在一般的に使われているような多層のニューラルネットワークにおいては、中間層の活性化関数にシグモイド関数は使われなくなりました。

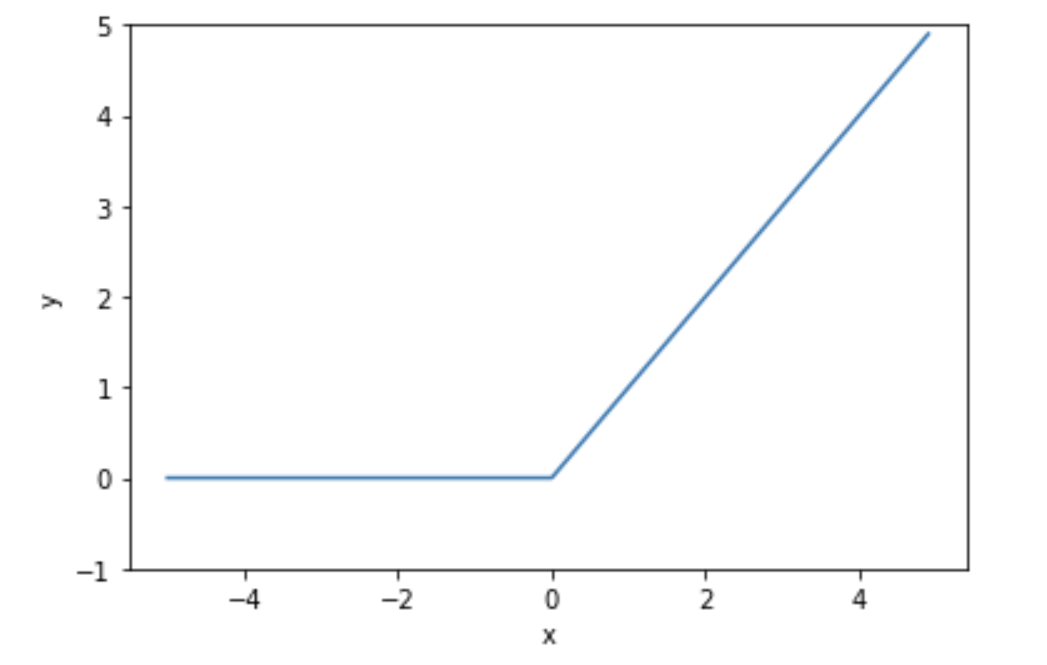
ReLU

現在中間層で使用される主流な活性化関数が、このReLU (Rectified Linear Unit) です。
入力が$0$を超えた時は入力をそのまま出力し、入力が$0$以下の時は$0$を出力します。

y = \left\{
\begin{array}{ll}
x & (x > 0) \\
0 & (x \leq 0)
\end{array}
\right.

ReLU

def relu(x):
    y = np.maximum(0, x)
    return y

　　　　　　　　　　　　　

ニューラルネットワークの逆伝播計算時、出力層 → 入力層に向かって（出力層の損失関数で算出した）誤差の情報を伝えていくのですが、その誤差の情報に、中間層の関数の微分値（勾配）を掛けていく計算を入力層まで繰り返していきます。
そこで勾配が$1$未満の値になってしまうと、出力層 → 入力層に向かって勾配を掛け合わせていく過程で、入力層に向かって伝える勾配がどんどん小さくなっていきます。
伝わる勾配が小さくなると、モデルの各パラメータ（重み・バイアス等）がほとんど更新されなくなってしまい、結果的にモデルの学習が上手くいかなくなってしまいます。（この現象を勾配消失といいます）

シグモイド関数は微分値（勾配）の最大が$0.25$のため、中間層の活性化関数に先程のシグモイド関数を用いると、逆伝播計算時の出力層 → 入力層に向かって勾配を掛け合わせていく過程で、勾配がどんどん小さくなります。　
一方ReLUの場合は、入力が$0$を超えていれば（$x>0$の場合）、逆伝播時の微分値（勾配）は$1$になるため、出力層 → 入力層に向かって勾配を掛け合わせていく過程で値が小さくならずに済みます。

微分（偏微分）を用いた逆伝播計算・勾配消失については、別記事（「ディープラーニング基礎理論_逆伝播編」）にて計算グラフ・数式を用いてより詳細に説明する予定です。

出力層の設計

次にニューラルネットワークの出力層についてです。
出力層では、入力層から伝わってきた入力を活性化関数に通すことで、最終的な値を出力します。
出力層における活性化関数として、「恒等写像関数」「シグモイド関数」「ソフトマックス関数」の3点を挙げます。

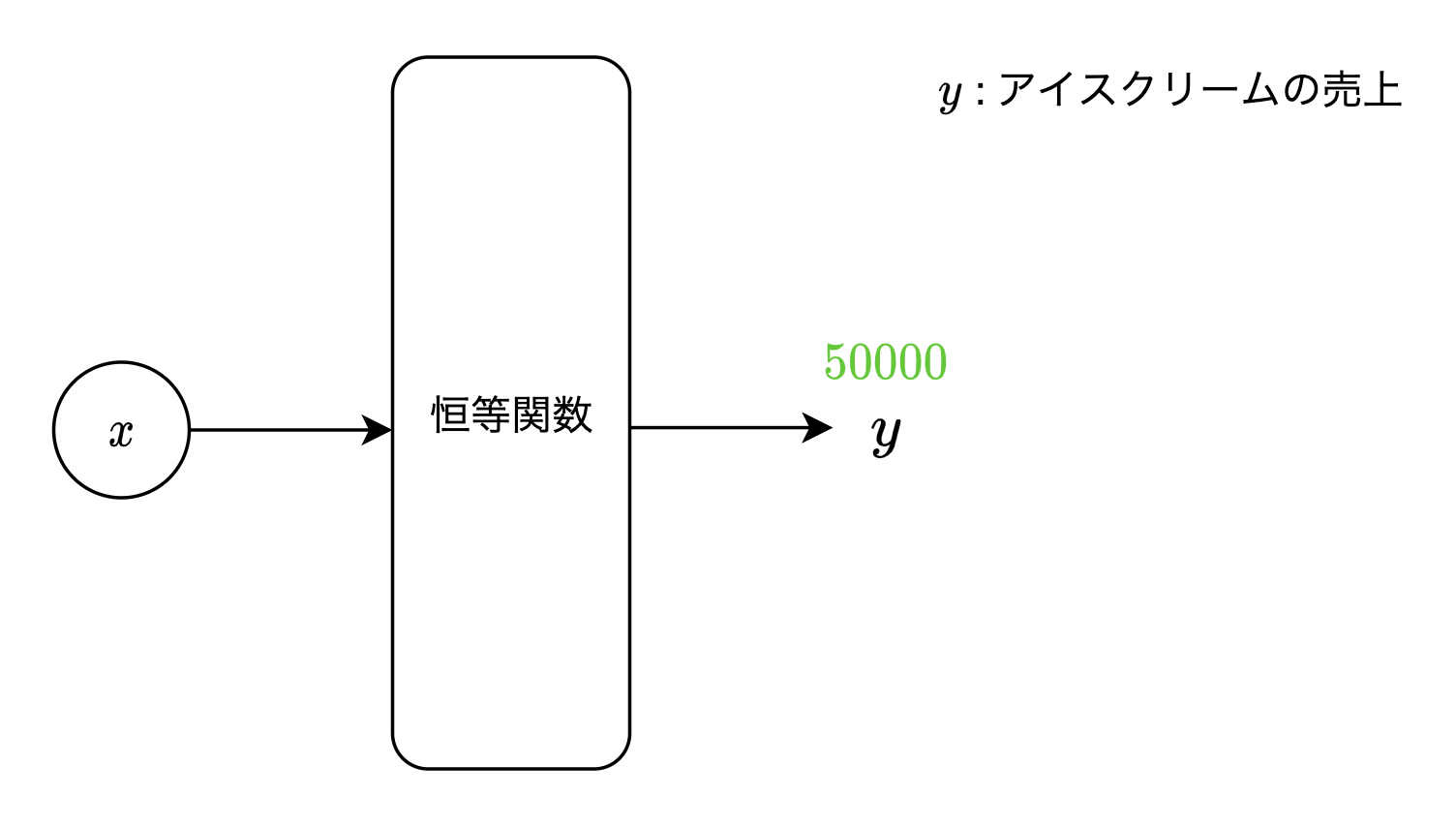
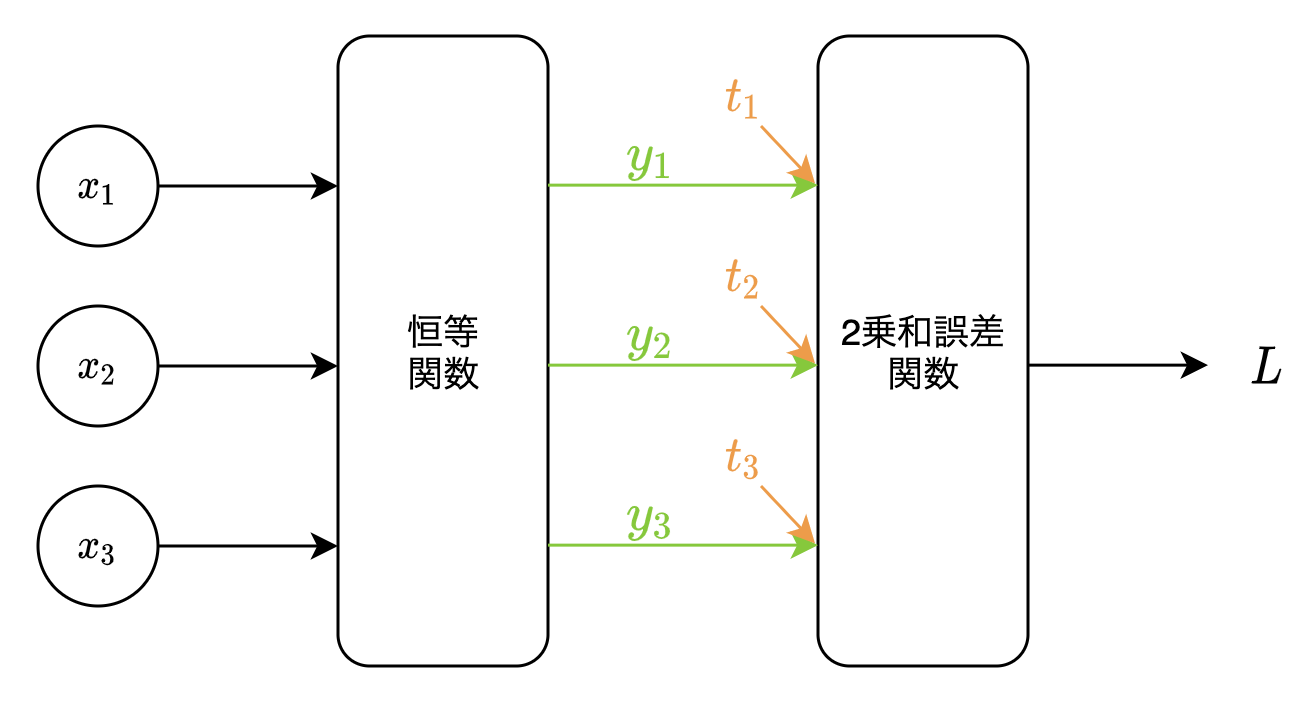
恒等関数

回帰問題（入力結果として、連続的な実数値を予測する問題）で用いられる活性化関数です。
入力された値をそのまま出力します。

y = x

恒等関数

def linear(x):
    return x

　　　　　　　　

$ex)$ 明日の「アイスクリームの売上」を予測するモデルに対し、説明変数（明日の「気温」「天気」など）を入力した結果、$50000$と出力されたとき、当モデルは明日のアイスクリームの売上が$5$万円と予測したことになります。

　　　　　　　　

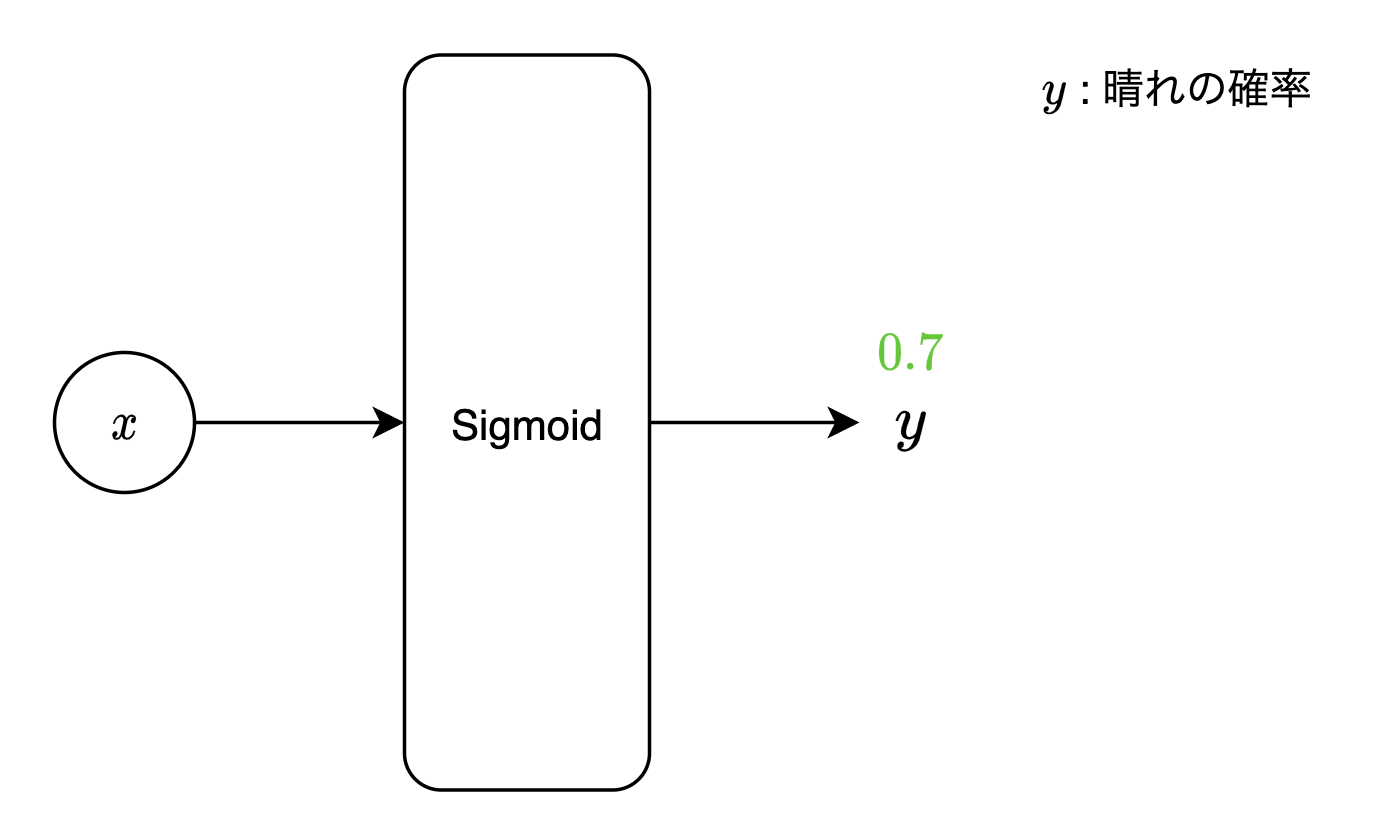
シグモイド関数

先程中間層の活性化関数として挙げましたが、出力層においては、2クラス分類問題（入力結果として、2つのクラスの内どちらのクラスに属するか分類する問題）で用いられます。

$ex)$ 出力層の1ノードに、明日の天気が「晴れ」と対応させます。明日の天気を予測するための説明変数（今日の「気温」「湿度」など）をモデルに入力することで、出力層のノードの出力値が$0.7$となったとき、当モデルは明日の天気が「晴れの確率：$70%$」「晴れでない確率：$30%$」と予測した、と見なせます。（求めたい確率$=p$とした時、それ以外の確率$=1-p$というように、2クラス分類できます（当例の場合、「晴れ」か「晴れでない」かの2クラスの内、$70%$と確率の大きい方である「晴れ」に、明日の天気を分類できます））

　　　　　　　　

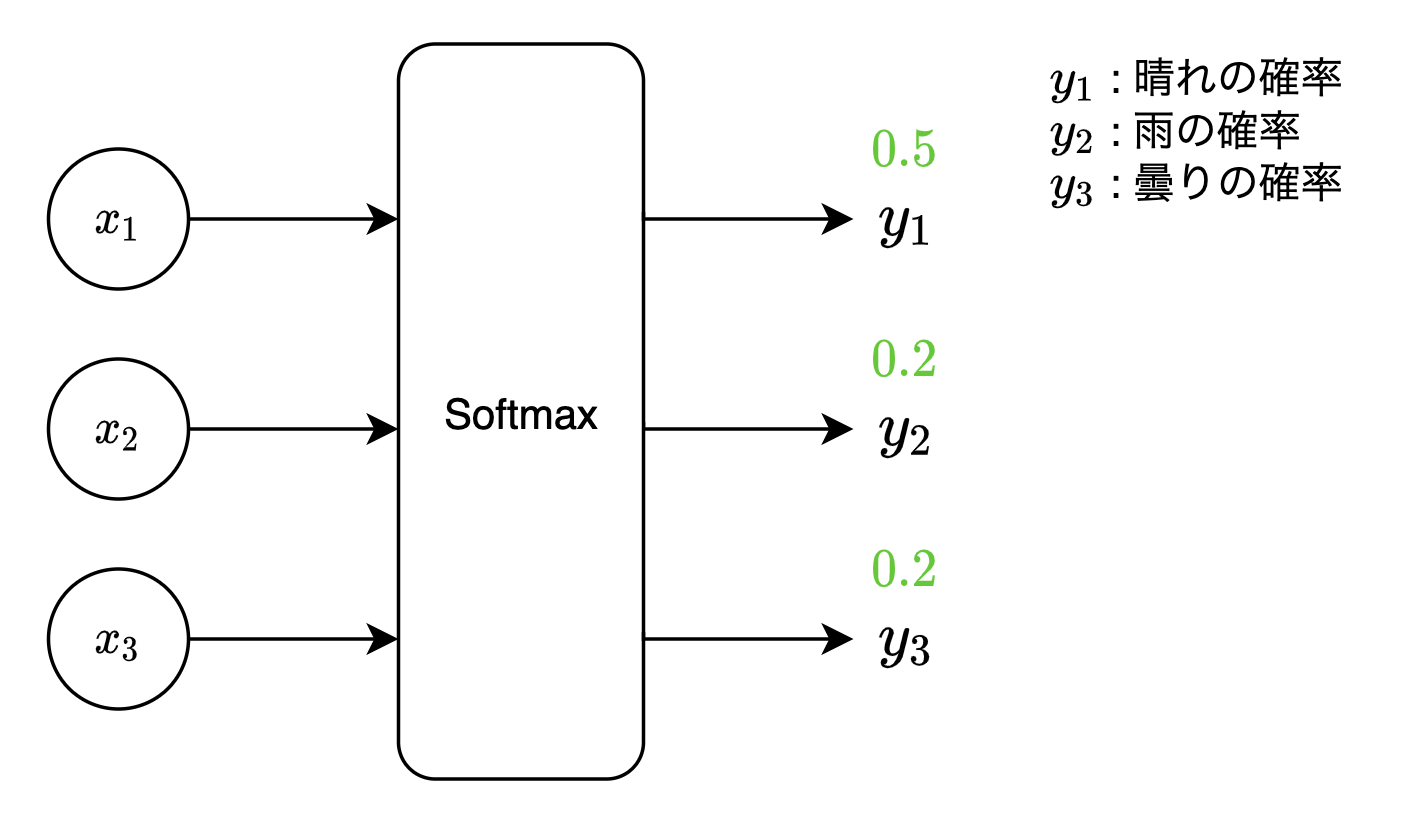
ソフトマックス関数

複数の入力を正規化し、出力値の合計が$1$になるようにする関数です。
多クラス分類問題（入力結果として、3つ以上のクラスの内どのクラスに属するか分類する問題）で用いられます。
出力値の合計が$1$になるため、各ノードに対応する出力値を確率と見なせます。

y_k = \frac{exp(x_k)}{\sum_{i=1}^{K}exp(x_i)}\\

$y_k$ : 出力層の$k$番目のノードに対応するソフトマックス関数の出力値
$K$ : 出力層のノード数
$k$ : 出力層のノード番号

ソフトマックス関数

def softmax(x):    
    return np.exp(x) / np.sum(np.exp(x))

実装上の注意点として、以下のように入力値に大きな値が入っている場合、指数関数の値が大きくなりすぎて、オーバーフローを引き起こします。

np.exp(1000) # inf になる
np.exp(1000) / (np.exp(1) + np.exp(1) + np.exp(1000)) # inf / inf = nan になる

オーバーフロー対策として、各入力値を入力の最大値で引く、ということをします。

ソフトマックス関数（オーバーフロー対策あり）

def softmax(x):
    a = np.max(x)
    return np.exp(x - a) / np.sum(np.exp(x - a))

$ex)$ 出力層のノードを3つ用意し、それぞれのノードに、明日の天気が「晴れ」「雨」「曇り」と対応させます。明日の天気を予測するための説明変数（今日の「気温」「湿度」など）をモデルに入力することで、出力層のノードの出力値がそれぞれ「晴れに対応するノード$=0.5$」「雨に対応するノード$=0.2$」「曇りに対応するノード$=0.3$」となったとき、当モデルは明日の天気が「晴れの確率：$50%$」「雨の確率：$20%$」「曇りの確率：$30 % $」と予測した、と見なせます。

　　　　　　　　

2クラス分類問題を多クラス分類問題と見なし、2クラス分類問題に対してソフトマックス関数を適用することもできますが、最適化するパラメータが多くなってしまうため、2クラス分類問題を解く場合は、基本的にシグモイド関数を用います。
（2クラス分類問題において、シグモイド関数を用いる場合は出力層は1ノードで済みますが、ソフトマックス関数を用いる場合は出力層が2ノードになります。結果的に、出力層の直前の重みの数が2倍になります。）

また、推論時では、出力層のソフトマックス関数を省略するのが一般的です。
推論時では、出力層としてソフトマックス関数を使う or 使わないで、結果は変わらない（ソフトマックス関数に通す前後で、値の大小関係は変わらない）ためです。
（学習時はパラメータ更新に使用する誤差を算出するために、出力を$0$-$1$間に収める処理が必要ですが、
推論時は、出力値の大小関係しか見ないため、わざわざソフトマックス関数に通す必要はありません。
結果が変わらないのであれば、計算負荷が余計にかかる処理を入れるべきではないです。）

損失関数

モデルの出力と正解データの間の誤差を算出するための関数です。
出力層にて、出力層で設定した活性化関数の直後に位置します。
（最終的なモデルの予測値である出力層の活性化関数の出力値と、正解データを入力とし、誤差を出力します。）
損失関数として一般的に用いられる「2乗和誤差関数」「クロスエントロピー誤差関数」の2点を挙げます。

2乗和誤差関数

回帰問題で用いられる損失関数です。

L = \frac{1}{2} \sum_{k=1}^{K}(y_k -t_k)^2

$L$ : 損失関数
$K$ : 出力層のノード数
$k$ : 出力層のノード番号
$y_k$ : $k$番目のノードの出力値
$t_k$ : $k$番目のノードの正解値

2乗和誤差関数

def squared_error(y, t):
    # y : 出力値
    # t : 正解値
    return 1/2 * np.sum((y - t)**2)

$1/2$を掛けている理由は、逆伝播計算時にこの2乗和誤差関数を微分したときに出てくる$\times2$を打ち消すためです。

実際にモデルに入力されるデータは1つではなく、複数個のまとまり（バッチ）であるため、以下のようにバッチ対応させる必要があります。

\begin{align}
L &= \frac{1}{N} \sum_{n=1}^{N} \bigl( \frac{1}{2} \sum_{k=1}^{K}(y_{nk} -t_{nk})^2 \bigl)\\
 &= \frac{1}{2N} \sum_{n=1}^{N}  \sum_{k=1}^{K}(y_{nk} -t_{nk})^2
\end{align}

$L$ : 損失関数
$N$ : データ数
$n$ : データ番号
$K$ : 出力層のノード数
$k$ : 出力層のノード番号
$y_{nk}$ : $n$番目のデータの、$k$番目のノードの出力値
$t_{nk}$ : $n$番目のデータの、$k$番目のノードの正解値

2乗和誤差関数（バッチ対応版）

def mean_squared_error(y, t):
    # y : 出力値
    # t : 正解値
    if y.ndim == 1:
        t = t.reshape(1, -1)
        y = y.reshape(1, -1)

    batch_size = y.shape[0]
    return 1/2 * np.sum((y - t)**2) / batch_size

また、出力値（出力層のノード数）が1つである、ある1つの実数値を予測する（一般的な）回帰問題では、以下のように、$K$は$1$になります。

L = \frac{1}{2N} \sum_{n=1}^{N}  \sum_{k=1}^{1}(y_{nk} -t_{nk})^2

回帰問題においては一般的に、出力層の恒等関数と2乗和誤差関数はセットで用いられます。

　　　　　　　　

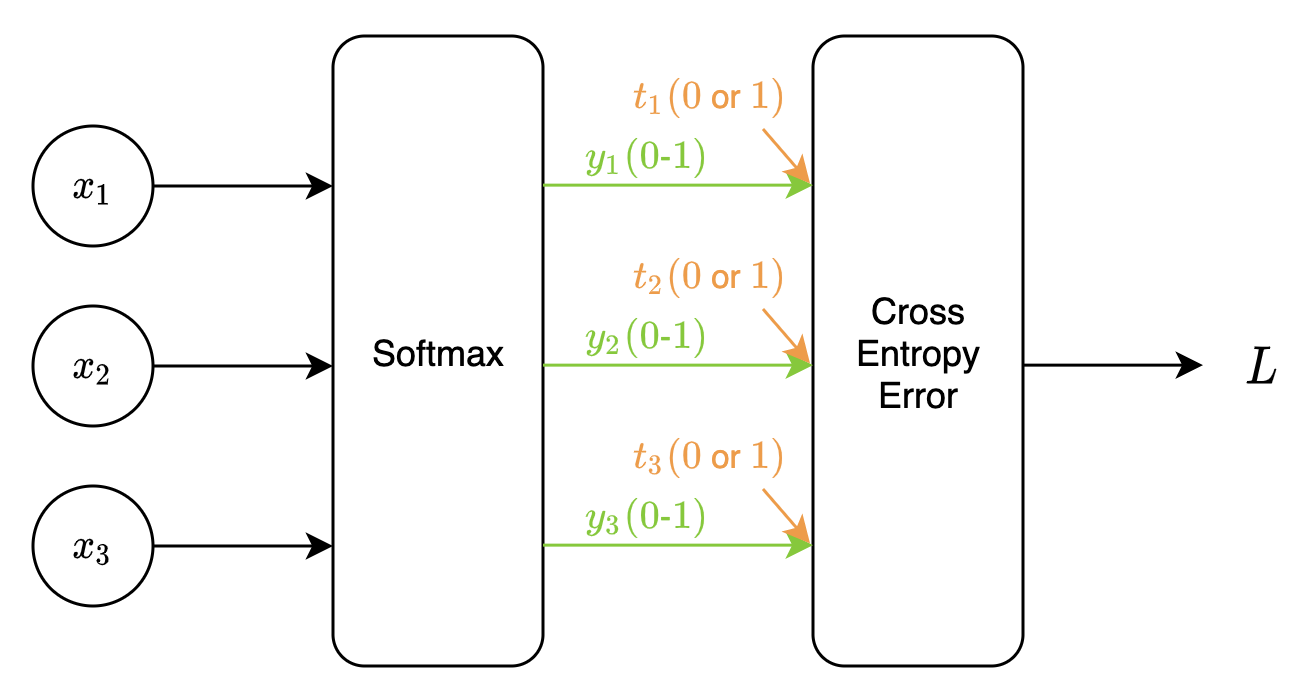
クロスエントロピー誤差関数

分類問題で用いられる損失関数です。

L = - \sum_{k=1}^{K} t_k \log y_k

$L$ : 損失関数
$K$ : 出力層のノード数
$k$ : 出力層のノード番号
$y_k$ : $k$番目のノードの出力値（$0$-$1$間の値をとる）
$t_k$ : $k$番目のノードの正解値（$0$or$1$）

$t_k$は出力層の各ノードに対応させる正解値であり、全ノードの内正解ノードに対応させる$t_k$が$1$、それ以外のノードに対応させる$t_k$が$0$、になります。
（$t_1 \cdots t_k$をまとめた「ある1つの要素のみが$1$、それ以外の要素が$0$のベクトル」である$\boldsymbol{t}$のことを、One-hotベクトルといいます）

関数の意味としては、
$1$（正解ノード）である$t_k$と対応する$y_k$の値のみが採用され、それ以外の$0$である$t_k$と対応する$y_k$の値は無視されます。（$0$である$t_k$と対応する$y_k$は$0$になり、$1$である$t_k$と対応する$y_k$のみが$L$の値に使われます。）

マイナスを掛けている理由ですが、
まず、出力値$y$が正解値$t$に近づくほど、$\sum$以降の部分は大きくなります。
一方、$L$は出力値と正解値の誤差なので、$L$の値は小さくしたい対象です（出力値$y$が正解値$t$に近づくほど$L$の値は小さくなってほしいです）。
そのため、最終的な値に対してマイナスを付けることで、出力値$y$が正解値$t$に近づくほど、誤差である$L$の値が小さくなるように表現しています。

クロスエントロピー誤差関数

def cross_entropy_error(y, t):
    delta = 1e-7 # 微小値
    return -np.sum(t * np.log(y + delta))

対数関数は入力に$0$をとれない（コード上ではnanになる）ため、$0$が含まれ得る出力値$y$に、微小値$delta$を足す必要があります。

# 正解データ
t = np.array([0, 0, 0, 1, 0]) # One-hotベクトル

# 予測データ1
y1 = np.array([0.1, 0.05, 0.6, 0.2, 0.05]) # 合計は1.0
print(cross_entropy_error(y1,t)) # 1.6094374124342252

# 予測データ2
y2 = np.array([0.1, 0.05, 0.2, 0.6, 0.05]) # 合計は1.0
print(cross_entropy_error(y2,t)) # 0.510825457099338

予測データ$y1,y2$は、ソフトマックス関数の出力のため、合計が$1$になります。
正解データでは、3番目の要素が$1$になっていますが、これは、入力データに対する正解クラスが、出力層の4番目のノードに対応していることを表します。
そして、正解である4番目のノードの出力値が小さい$y1$のクロスエントロピー誤差は大きく、4番目のノードの出力値が大きい$y2$のクロスエントロピー誤差は小さくなります。

2乗和誤差同様、バッチ対応させる場合は、以下のようになります。

\begin{align}
L &= \frac{1}{N} \sum_{n=1}^{N}(- \sum_{k=1}^{K} t_{nk} \log y_{nk})\\
&= -\frac{1}{N} \sum_{n=1}^{N} \sum_{k=1}^{K} t_{nk} \log y_{nk}
\end{align}

$L$ : 損失関数
$N$ : データ数
$n$ : データ番号
$K$ : 出力層のノード数
$k$ : 出力層のノード番号
$y_{nk}$ : $n$番目のデータの、$k$番目のノードの出力値（$0$-$1$間の値をとる）
$t_{nk}$ : $n$番目のデータの、$k$番目のノードの正解値（$0$or$1$）

クロスエントロピー誤差関数（バッチ対応版）

def mean_cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, -1)
        y = y.reshape(1, -1)
        
    batch_size = y.shape[0]
    delta = 1e-7 # 微小値
    return -np.sum(t * np.log(y + delta)) / batch_size

また、出力層に用いる活性化関数がシグモイド関数（2クラス分類問題）の場合、出力値（出力層のノード数）は1つのため、以下のように、$K$は$1$になります。

L = -\frac{1}{N} \sum_{n=1}^{N} \sum_{k=1}^{1} t_{nk} \log y_{nk}

分類問題においては一般的に、出力層のソフトマックス関数とクロスエントロピー誤差関数はセットで用いられます。

　　　　　　　　

全体サンプルコード

以下は多クラス分類（3クラス分類）を行うニューラルネットワーク全体（順伝播計算・誤差の算出のみ）のサンプルコードです。
ニューラルネットワーク全体の、順伝播計算・誤差の算出の流れを示すことが目的のため、以下の点にご注意ください。

• 実行サンプルを含めると、ネットワーク構成は以下になります。
  • 中間層：3層
  • ノード数はそれぞれ、入力層数：4、第1層目の中間層：3、第2層目の中間層：2、出力層：3
• また実行サンプルについてですが、入力データと正解データに意味は持たせていません。
• 学習を行っていないため、誤差は大きいです。
• コード内で使用している活性化関数・損失関数は、当記事内のコードを用いています。

neural_network

class neural_network:
    def __init__(self, input_size, hidden_size, output_size):            
        self.W1 = np.random.randn(input_size, hidden_size[0])
        self.b1 = np.zeros(hidden_size[0])
        self.W2 = np.random.randn(hidden_size[0], hidden_size[1])
        self.b2 = np.zeros(hidden_size[1])
        self.W3 = np.random.randn(hidden_size[1], output_size)
        self.b3 = np.zeros(output_size)
    
    def predict(self, X):
        A1 = relu(np.dot(X, self.W1) + self.b1)
        A2 = relu(np.dot(A1, self.W2) + self.b2)
        Y = softmax(np.dot(A2, self.W3) + self.b3)
        return Y
    
    def loss(self, X, T):
        Y = self.predict(X)
        loss = mean_cross_entropy_error(Y, T)
        print(Y.shape)
        return loss

実行サンプル

n = 5 # データ数
input_size = 4 # 入力層のノード数
hidden_size = [3,2] # 中間層のノード数
output_size = 3 # 出力層のノード数

# 入力データ : データ形状 = (5,4)
X = np.arange(n * input_size).reshape(n, input_size)

# 正解データ : データ形状 = 出力層で出力される予測データと同じ(5,3)
T = np.array([[1,0,0],
              [0,1,0],
              [0,1,0],
              [0,0,1],
              [0,1,0]])

model = neural_network(input_size, hidden_size, output_size)
loss = model.loss(X, T)
print(loss)

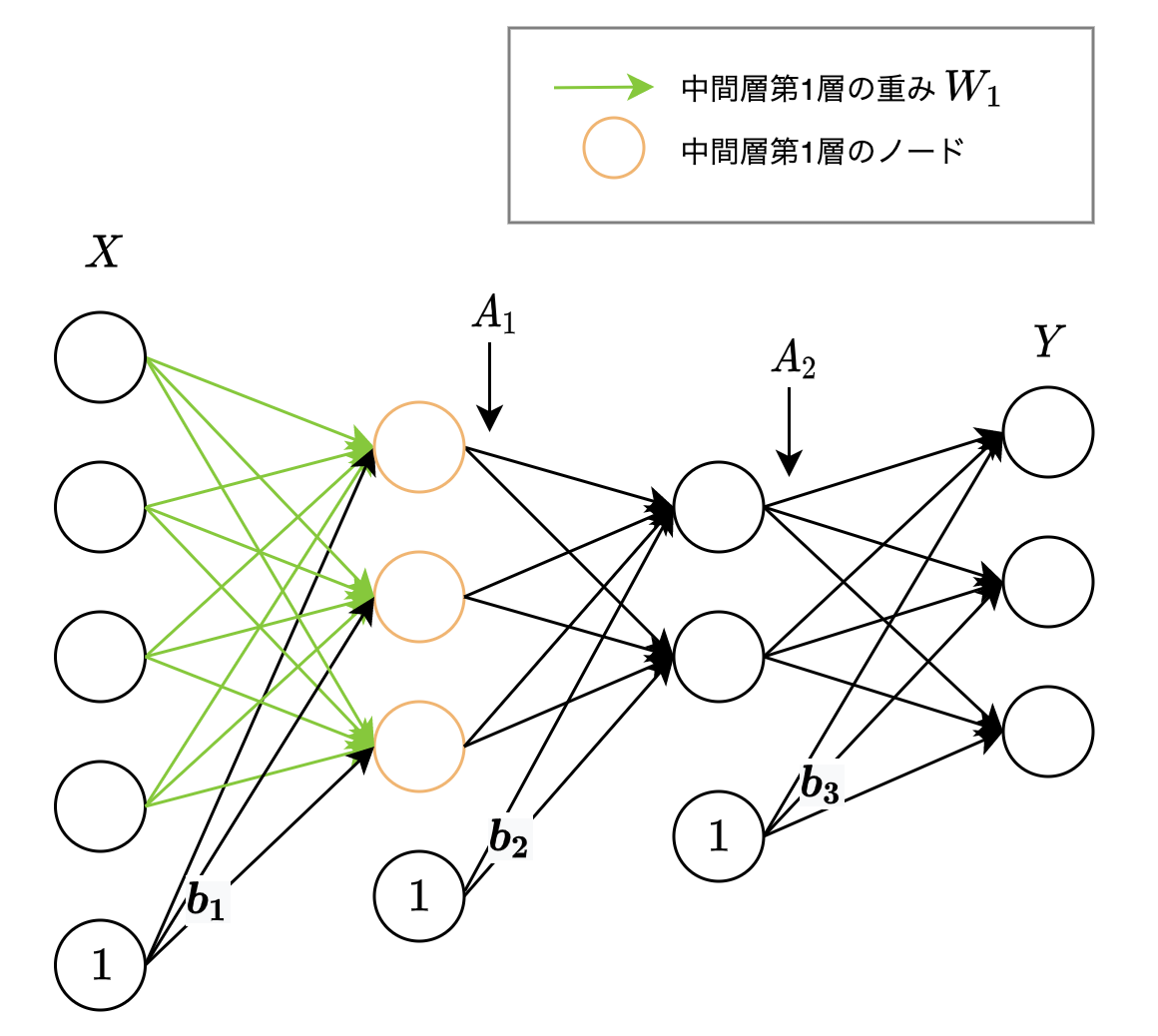
注意すべきポイントは、各データの形状です。
入力データ・重み・バイアス・出力データの行列形状は以下になります。

・入力データ $=$ (入力データ数, 入力層のノード数)
・中間層第1層の重み $=$ (入力層のノード数, 中間層第1層のノード数)
・中間層第1層のバイアス $=$ (中間層第1層のノード数,)
・中間層第2層の重み $=$ (中間層第1層のノード数, 中間層第2層のノード数)
・中間層第2層のバイアス $=$ (中間層第2層のノード数,)
・中間層第3層（出力層直前）の重み $=$ (中間層第2層のノード数, 出力層のノード数)
・中間層第3層（出力層直前）のバイアス $=$ (出力層のノード数,)
・出力データ $=$ (入力データ数, 出力層のノード数)

中間層における重み・バイアスの行列形状を一般化すると、以下になります。
・重み $=$ (前層のノード数, 現層のノード数)
・バイアス $=$ (現層のノード数,)

また、入力データ・および各層の出力データの行列形状について補足ですが、
第1要素はデータサイズに、第2要素は各層のノード数になります。（各層における「ノード数」の実体は、各層の出力データの1データ（ベクトル）の要素数のことです）

　　　　　　　　

モデル構成は、以下のようになります。

　　　　　　　　

参考

• ゼロから作るDeep-Learning-―Pythonで学ぶディープラーニングの理論と実装