これは、Visual Basic Advent Calendar 2016の7日目の記事です。
1. テーマ
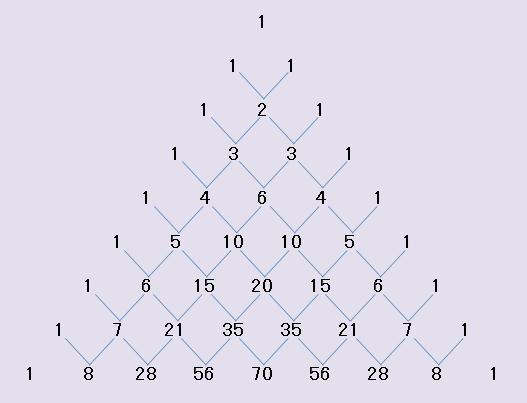
これまで何度かQiitaで紹介してきたVBAHaskellでちょっとしたデモみたいなことができないかと考えて、パスカルの3角形を作ってみることにしました。
高校数学の順列・組み合わせや二項定理で出てきたこれです。
最上段が1で1段ずつ下に伸びていきます。隣どうしの数を足して下の段を作っているだけなので、どんな言語でもプログラムを書くのは簡単だと思いますが、これをVBAHaskellの既存の関数だけを使ってなるべく短く書くことを目標とします。標準モジュール等に何もコードを追加せず、イミディエイト ウィンドウ上だけで行います。
VBAHaskellのモジュール自体は下のリンクに置いてあります。
2. 方針
まず、「配列の隣どうしの要素の間で何かする」のにぴったりのadjacent_opという関数があるのでこれを使います。
' 1次元配列vecの隣接する要素間で2項操作 op を行う
' 出力列の要素数は 元の要素数 -1
Function adjacent_op(ByRef op As Variant, ByRef vec As Variant) As Variant
たとえば 配列{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}の隣どうしの和であれば{3 ,5 ,7 ,9 ,11 ,13 ,15 ,17 ,19}ができ、積であれば{2 ,6 ,12 ,20 ,30 ,42 ,56 ,72 ,90}ができます。
a = iota(1,10) ' iota は連続する数値の配列を作る関数
printM a ' printM はイミディエイトウィンドウに配列を出力
1 2 3 4 5 6 7 8 9 10 ' <= 長さ10
b = adjacent_op(p_plus, a) ' p_plus は加法 +
printM b
3 5 7 9 11 13 15 17 19 ' <= 長さ9
c = adjacent_op(p_mult, a) ' p_mult は乗法 *
printM c
2 6 12 20 30 42 56 72 90 ' <= 長さ9
和(p_plus)や積(p_mult)はVBAHaskellで標準関数として用意されているものですが、ユーザーが独自の2項演算を定義してadjacent_opに渡すこともできます。
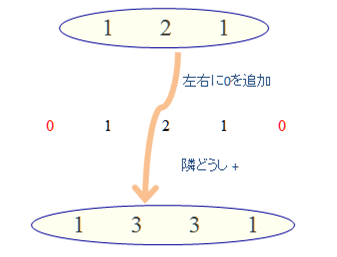
隣どうしで演算するので、配列の長さは1つぶん短くなります(10から9に減)。パスカルの三角形を作るには下に行くほど1つずつ長くしなければいけません。その方法としては 配列の左右に0を追加してからadjacent_opを実行する ことにします。
3. 関数を合成する
VBAHaskellは関数型っぽいプログラムを書けることを目指していて、関数の引数として関数(のようなもの)を渡したり、複数の関数を合成・ネストして関数を作ったり、関数の引数を束縛して2変数関数を1変数関数にしたりすることができます。
前のセクションで書いた方針通りに、配列の左に0を追加する ![]() 配列の右に
配列の右に0を追加する ![]() 加法(+)で
加法(+)でadjacent_opする、という手続きを表す関数で作ってみましょう。
結論を先に書くと、それはこういう形になります。
f = p_adjacent_op(p_plus, p_catV(p_catV(0), 0))
使われている3つの関数はどれも2変数関数です。
| 関数本体 | p_関数 | 機能 |
|---|---|---|
| adjacent_op | p_adjacent_op | 隣どうしの2項演算適用 |
| plus | p_plus | 加法演算(a+b) |
| catV | p_catV | 2個の1次元配列を結合 |
**「関数本体」は普通のVBA関数で「p_関数」**はそのアドレス(AddressOfの値)を含む一種の関数オブジェクトです(実体は配列)。VBAHaskellは多くの関数とその関数オブジェクトをペアにして実装しています。例えばp_appleという関数が出てきたらappleという関数があってそちらが本体だと思ってください。
上記ではそれらが合成されており、一部の引数に0が置かれています。デフォルト引数として隠れているところも含めてこの関数オブジェクトを模式的に書くとこんな構造になっています。
f = p_adjacent_op( p_plus( ___ , ___ ) , p_catV( p_catV( 0 , _![]() _ ), 0 ) )
_ ), 0 ) )
_![]() _ の個所はプレースホルダで、後から引数が入る場所です。そこに1次元配列
_ の個所はプレースホルダで、後から引数が入る場所です。そこに1次元配列vが入ると catV(catV(0, v), 0) となるので、vの左右に0を追加する動作になります。p_plusの引数にある__も同じくプレースホルダです。
**「後から」**というのがポイントで、f = p_adjacent_op(...)という式を実行した時点ではまだ計算本体は行われていません。fを実際に動かすのはHaskell_0_declareモジュールやHaskell_1_Coreモジュールにある一部の関数の役割です。
ちなみに、0を追加するのを左→右の順ではなくて右→左の順にしたければ以下のように書きます。
f = p_adjacent_op(p_plus, p_catV(0, p_catV(, 0)))
では、この合成された関数を実際に動かしてみましょう。初期値はArray(1)です。
4. 繰り返し処理
パスカルの三角形は無限に続いていくので、実際のプログラムは「第N段まで」という形で表すことにします。
単純に繰り返し処理を行う関数として、現状VBAHaskellに4つの関数を用意しています。
| 関数 | 機能 |
|---|---|
| repeat_while | 条件が満たされる間繰り返し関数適用 |
| repeat_while_not | 条件が満たされない間繰り返し関数適用 |
| generate_while | 条件が満たされる間繰り返し関数適用の履歴を生成 |
| generate_while_not | 条件が満たされない間繰り返し関数適用の履歴を生成 |
三角形の第N段目だけでなく、作った1段目~N段目の全体を履歴として表示したいので、3番目のgenerate_whileを使うことにします。
' 述語による条件が満たされる間繰り返し関数適用の履歴を生成
Function generate_while(ByVal val As Variant , _ ' ← 初期値
ByRef pred As Variant, _ ' ← 条件
ByRef fun As Variant , _ ' ← 関数
Optional ByVal n As Long = -1 _ ' ← 回数上限
) As Variant
2番目の引数は繰り返しを続ける条件ですが、特に条件は付けず回数指定=8で動かすとこうなります。
' 初期値配列 a
a = Array(1)
' 繰り返し適用する関数を定義
f = p_adjacent_op(p_plus, p_catV(p_catV(0), 0))
' f を繰り返し適用してその履歴を生成
result = generate_while(a, p_true, f, 8) ' p_true は恒真条件
' サイズを表示
printS result
[Dim1]: 0 -> 8 : Total Size = 9
' 個々の要素を表示
printM result ' ↓ ジャグ配列(配列の配列)なのでこうなる
[0] [1] [2] [3] [4] [5] [6] [7] [8]
' printM_ でジャグ配列の要素を順に表示
printM_ result
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
少し長いですが1行のコードにすることもできます。
printM_ generate_while(Array(1), p_true, p_adjacent_op(p_plus, p_catV(p_catV(0), 0)), 8)
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
5. 他の書き方(1)
大して変わりばえしませんが、generate_whileに回数上限ではなく終了条件を指定してみます。第2引数に「長さがN未満だったら続ける」という条件を与えるバージョンがこちらです。
' a と f は前のと同じ
printM_ generate_while(a, p_less(p_sizeof, 8), f)
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
lessは「小なり比較(a < b)」関数、sizeofは配列の長さを取得する関数です。
p_sizeofにデフォルト引数が隠れていて p_less( p_sizeof( _![]() _ ) , 8 ) ) という構造になっているので、プレースホルダ(_
_ ) , 8 ) ) という構造になっているので、プレースホルダ(_![]() _)のところに
_)のところに v が代入されると、less(sizeof(v), 0) すなわち「配列vの長さ < 8」の判定結果が返ってきます。
これが満たされるのは7段目の{1 ,6 ,15 ,20 ,15 ,6 ,1}のところまでで、満たされなくなった8段目のところで止まる仕組みです。条件が満たされる限り無限ループになるので少し危険です。
6. 他の書き方(2)
ただのループではなく、もうちょっとHaskellっぽいfold/scan系の関数を使ってみます。
| 関数 | 機能 |
|---|---|
| foldl | 左畳み込み(初期値指定あり) |
| foldr | 右畳み込み(初期値指定あり) |
| foldl1 | 左畳み込み(初期値=先頭要素) |
| foldr1 | 右畳み込み(初期値=末尾要素) |
| scanl | 左scan(初期値指定あり) |
| scanr | 右scan(初期値指定あり) |
| scanl1 | 左scan(初期値=先頭要素) |
| scanr1 | 右scan(初期値=末尾要素) |
fold(畳み込み)というのは2項関数を列の全要素にわたって順に実行していくやり方のひとつで、列の左側から処理していくfoldlと右側から処理していくfoldrに分かれます。 |
関数fと初期値#, 列{a, b, c, ... , x, y, z}があるとして、foldlはa, b, c, ... の順に関数に食べさせていきます。
f(...(f(f(f(#,a),b),c),...),x),y),z)
foldrは逆にz, y, xの順に食べていきます。
f(a,f(b,f(c, ..., f(x,f(y,f(z,#)))...)))
' foldl で 0 から {1, 2, ..., 10} を足していった合計値を出す
printM foldl(p_plus, 0, iota(1, 10))
55
' scanl だと過程も得られる
printM scanl(p_plus, 0, iota(1, 10))
0 1 3 6 10 15 21 28 36 45 55
scan系は結果だけでなく、畳みこみの過程をすべて保持して返すもので、今回はこれを使います。
ここで発想を逆転させて、データではなくて関数fの方が{f, f, f, ... , f}と並んでいるとしましょう。
この列を上手く使えば、
((((初期値とfを作用させた結果)
とfを作用させた結果 ))
とfを作用させた結果)
・・・
という形で繰り返しを表現できます。
値xと関数fを作用させるとはつまりxとfからf(x)を導くことであり、それを行う関数applyFunが用意されています。
' 関数適用関数 1引数に対して関数を適用する
Function applyFun(ByRef param As Variant, _
ByRef func As Variant) _
As Variant
これをscanlに渡して左から順に{f, f, f,...}を渡していけば出来上がりです。
' repeat は同一データを任意の個数並べた配列を作る関数
' a と f は前のと同じ
printM_ scanl(p_applyFun, a, repeat(f, 8))
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
7. まとめ
イミディエイト ウィンドウ上でパスカルの三角形を表示するコードは88文字になりました。
printM_ generate_while(Array(1), p_true, p_adjacent_op(p_plus, p_catV(p_catV(0), 0)), 8)
関数合成と繰り返し処理の抽象化によって汎用部品だけで構成できました。しかしp_trueとかp_plusといった関数オブジェクトをライブラリ側にいちいち用意しておかなければならない点が不便です。ベース言語がVBAである以上どうしようもないのか、C++APIを含めたライブラリ側で何か工夫の余地はないか、もう少し考えないとわかりません。ただしコードの短さという点ではこのへんが限界なのではないかと思っています。
リンク
Qiita VBAHaskellの紹介 その1 (最初はmapF)
ソースコード(Github)
VBAHaskellの関数リファレンス
dllバイナリ:
https://github.com/mYmd/VBA/blob/master/bin/mapM (32bit-Office用)
https://github.com/mYmd/VBA/blob/master/bin/mapM64 (64bit-Officey用)
VBAコード添付済みExcelブック
VBAHaskellほぼ全部入り.xlsm