ラビットチャレンジ レポート（その12 深層学習Day4 Section1~4）

深層学習Day4

Section1 強化学習

強化学習とは、長期的に報酬を最大化できるように環境の中で行動を選択できるエージェントを作ることを目標とする機械学習の一分野。
行動の結果として与えられる利益を元に行動を決定する原理を改善していく仕組み。

簡単な概念図は以下。

強化学習の応用例

例えば、マーケティングの場合。

• 環境：会社の販売促進部
• エージェント：プロフィールと購入履歴に基づいて、キャンペンメールを送る顧客を決めるソフトウェア
• 行動：顧客ごとに送信、非送信の二つの行動が選択肢
• 報酬：キャンペーンのコストという負の報酬とキャンペーンで生み出される推測される売上という正の報酬

探索と利用のトレードオフ

環境について事前に完全な知識があれば、最適な行動を予測し決定することは可能。
（先ほどの例では、どのような顧客にキャンペンメールを送信すると、どのような行動を行うのかが既知である状況）

しかし、強化学習ではこの仮定は成り立たないとする。
不完全な知識を元に行動をしつつデータを集めて、最適な行動を見つけていく。

探索が足りない状態（過去のデータでベストとされる行動のみを取り続ければ他の行動を見つけられない。）と、利用が足りない状態（未知の行動のみを常に取り続ければ、過去の経験が活かせない。）はトレードオフの関係。

強化学習と教師あり/なし学習の違い

目的が違う。
教師あり/なし学習では、データの特徴量から、データに当てはまるパターン（法則）を見つけ出し、汎化性能を持つモデルを作り、データから推測行うことが目標。
一方強化学習では、優れた方策を見つけることが目標。

価値関数

強化学習の概念において、価値を表す関数のこと。
2種類あって、
ある状態の価値に注目する場合は状態価値関数
状態と価値を組み合わせた価値に注目する場合は行動価値関数

方策関数

方策ベースの強化学習手法において、ある状態でどのような行動を採るかの確率を与える関数のこと。

方策勾配法

方策をモデル化して最適化する方法。
式で表すと以下。

\theta^{(t+1)} = \theta^{(t)} + \epsilon \nabla J(\theta)

この式における$J$は方針の良さを表す。これはモデルを作る際に定義する必要がある。
定義方法は、平均報酬と割引報酬和の2つ。
この定義に対して、行動価値関数$Q(s,a)$の定義を行う。
このとき、以下の方策勾配定理が成り立つ。

\nabla _{\theta} J(\theta) = \mathbb{E}_{\pi_{\theta}} [(\nabla_{\theta} \log{\pi_{\theta}}(a|s) Q^{\pi} (s,a))]

実装演習

CartPoleで強化学習を試す。

import gym
import numpy as np

env = gym.make('CartPole-v0') # 環境に相当するオブジェクトをenvとおく。

goal_average_steps = 195 # 195ステップ連続でポールが倒れないことを目指す
max_number_of_steps = 200 # 最大ステップ数
num_consecutive_iterations = 100 # 評価の範囲のエピソード数
num_episodes = 5000
last_time_steps = np.zeros(num_consecutive_iterations)

# 価値関数の値を保存するテーブルを作成する。
# np.random.uniformは指定された範囲での一様乱数を返す。
q_table = np.random.uniform(low=-1, high=1, size=(4**4, env.action_space.n))

def bins(clip_min, clip_max, num):
    return np.linspace(clip_min, clip_max, num + 1)[1:-1]
    # np.linspaceは指定された範囲における等間隔数列を返す。

def digitize_state(observation):
    # 各値を４個の離散値に変換
    # np.digitizeは与えられた値をbinsで指定した基数に当てはめる関数。インデックスを返す。
    cart_pos, cart_v, pole_angle, pole_v = observation
    digitized = [np.digitize(cart_pos, bins=bins(-2.4, 2.4, 4)),
                 np.digitize(cart_v, bins = bins(-3.0, 3.0, 4)),
                 np.digitize(pole_angle, bins=bins(-0.5, 0.5, 4)),
                 np.digitize(pole_v, bins=bins(-2.0, 2.0, 4))]

    # 0~255に変換
    return sum([x* (4**i) for i, x in enumerate(digitized)]) # インデックス付きループをすることができる。


def get_action(state, action, observation, reward, episode):
    next_state = digitize_state(observation)
    epsilon = 0.5 * (0.99** episode)
    if epsilon <= np.random.uniform(0, 1): # もし一様乱数のほうが大きければ
        next_action = np.argmax(q_table[next_state])# q_tableの中で次に取りうる行動の中で最も価値の高いものを
                                                    # next_actionに格納する
    else:# そうでなければ20%の確率でランダムな行動を取る
        next_action = np.random.choice([0, 1])


    # Qテーブルの更新
    alpha = 0.2
    gamma = 0.99
    q_table[state, action] = (1 - alpha) * q_table[state, action] + \
            alpha * (reward + gamma * q_table[next_state, next_action])
    return next_action, next_state

step_list = []
for episode in range(num_episodes):
    # 環境の初期化
    observation = env.reset()

    state = digitize_state(observation)
    action = np.argmax(q_table[state])

    episode_reward = 0
    for t in range(max_number_of_steps):
        env.render() # CartPoleの描画

        observation, reward, done, info = env.step(action) # actionを取ったときの環境、報酬、状態が終わったかどうか、デバッグに有益な情報

        if done: # 倒れた時罰則を追加する
            reward -= 200
        # 行動の選択
        action, state = get_action(state, action, observation, reward, episode)
        episode_reward += reward


        if done:
            print('%d Episode finished after %f time steps / mean %f' %
                (episode, t + 1, last_time_steps.mean()))
            last_time_steps = np.hstack((last_time_steps[1:], [t+1]))
            # 継続したステップ数をステップのリストの最後に加える。np.hstack関数は配列をつなげる関数。
            step_list.append(t+1)
            break

    if (last_time_steps.mean() >= goal_average_steps): # 直近の100エピソードの平均が195以上であれば成功
        print('Episode %d train agent successfully!' % episode)
        break

Section2 AlphaGo

AlphaGoはGoogle DeepMindによって開発されたコンピュータ以後プログラム。強化学習の仕組みを用いている。
2015年には、ハンデなしで初めて人間のプロ囲碁棋士を破ったことで話題になった。

AlphaGoの方策関数が以下。

AlphaGoの価値関数が以下。

方策関数・価値関数の入力は以下。

NNではなく、線形の方策関数。
PolicyNetでは学習に時間がかかるため、こちらを用いるが、精度は少し落ちる。

AlphaGoの学習

AlphaGoは3段階で学習される。
①教師あり学習による、RollOutPolicyとPolicyNetの学習
②強化学習によるPolicyNetの学習
③強化学習によるValueNetの学習

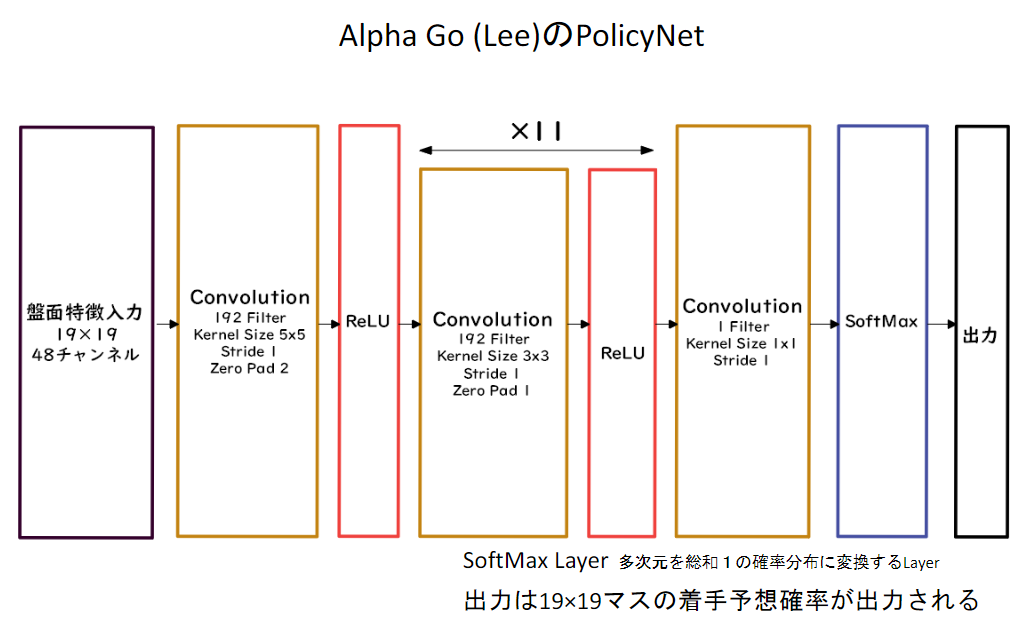
PolicyNetの教師あり学習

KGS Go Serverの棋譜データから3000万局面分の教師データを用意し、教師と同じ着手を予測できるように学習を行った。
具体的には、教師が着手した手を1とし、残りを0とした19×19次元の配列を教師とし、それを分類問題として学習した。
この学習で作成したPolicyNetは57%ほどの精度である。

PolicyNetの強化学習

現状のPolicyNetとPolicyPoolからランダムに選択されたPolicyNetと対局シミュレーションを行い、その結果を用いて方策勾配法で学習を行った。PolicyPoolとは、PolicyNetの強化学習の過程を500Iteraionごとに記録し保存しておいたものである。現状のPolicyNet同士の対局ではなく、PolicyPoolに保存されているものとの対局を使用する理由は、対局に幅を持たせて過学習を防ごうというのが主である。
この学習をミニバッチサイズ128で1万回行った。

ValueNetの強化学習

PolicyNetを使用して対局シミュレーションを行い、その結果の勝敗を教師として学習した。
【教師データ作成の手順】
①まずSL PolicyNet(教師あり学習で作成したPolicyNet)でN手まで打つ。
②N+1手目の手をランダムに選択し、その手で進めた局面をS（N+1）とする。
③S（N+1）からRLPolicyNet（強化学習で作成したPolicyNet）で終局まで打ち、その勝敗報酬をRとする。

S(N+1）とRを教師データの対にして、回帰問題（誤差関数は平均二乗誤差）として学習した。この学習をミニバッチサイズ32で5000万回行った。
N手までとN+1手からのPolicyNetを別々にしてある理由は、過学習を防ぐためであると論文では説明されている。

AlphaGo Zero

AlphaGo ZeroはAlphaGoのバージョンの一つ。2017年に発表された。このバージョンのAlphaGoは人間同士の対局データ（棋譜）を一切使わずに作られているが、それまでのどのバージョンのAlphaGoよりも強かった。

AlphaGo(Lee)とAlphaGo Zeroの違い

• 教師あり学習を一切行わず、強化学習のみで作成
• 特徴入力からヒューリスティックな要素を排除し、石の配置のみにした
• PolicyNetとValueNetを１つのネットワークに統合した
• Residual Net（後述）を導入した
• モンテカルロ木探索からRollOutシミュレーションをなくした

ここにも出てきた、PolicyNetとValueNetを一つのネットワークに統合したPolicyValueNetが以下。

このPolicyValueNet中に出てくる、ResidualNetworkの部分の構造が以下。

このResidual Networkは、ネットワークにショートカット構造を追加して、勾配爆発・勾配消失を抑える効果を狙ったモノ。
画像認識のモデルとして、初めてResidual Netoworkと似たような構造を導入したResNetと同じような意味合いを持つ。
この構造を持つことによって、層数の違うNetworkのアンサンブル効果が得られているという説もある。

AlphaGo Zeroの学習

大きく分けると、
①自己対局による教師データの作成
②学習
③ネットワークの更新
の3ステップで構成される。

①自己対局による教師データの作成
現状のネットワークでモンテカルロ木探索を用いて自己対局を行う。まず30手までランダムで打ち、そこから探索を行い勝敗を決定する。自己対局中の各局面での着手選択確率分布と勝敗を記録する。教師データの形は（局面、着手選択確率分布、勝敗）が１セットとなる。

②学習
自己対局で作成した教師データを使い学習を行う。NetworkのPolicy部分の教師に着手選択確率分布を用い、Value部分の教師に勝敗を用いる。
損失関数は、Policy部分はCrossEntropy、Value部分は平均二乗誤差。

③ネットワークの更新
学習後、現状のネットワークと学習後のネットワークとで対局テストを行い、学習後のネットワークの勝率が高かった場合、学習後のネットワークを現状のネットワークとする。

実装演習

Residual Blockの部分をPytorchで実装してみる。

import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms

class ResidualBlock(nn.Module):
    def __init__(self, in_channels, out_channels, stride=1, downsample=None):
        super(ResidualBlock, self).__init__()
        self.conv1 = conv3x3(in_channels, out_channels, stride)
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.relu = nn.ReLU(inplace=True)
        self.conv2 = conv3x3(out_channels, out_channels)
        self.bn2 = nn.BatchNorm2d(out_channels)
        self.downsample = downsample
        
    def forward(self, x):
        residual = x
        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)
        out = self.conv2(out)
        out = self.bn2(out)
        if self.downsample:
            residual = self.downsample(x)
        out += residual
        out = self.relu(out)
        return out

Section3 軽量化・高速化技術

分散深層学習とは

深層学習は多くのデータを使用したり、パラメータ調整のために多くの時間を使用したりするため、高速な計算が求められる。
複数の計算資源を使用し、並列的にニューラルネットワークを構成することで、効率の良い学習を行いたい。
データ並列化・モデル並列化・GPUによる高速技術は不可欠である。

データ並列化

親モデルを各ワーカーに子モデルとしてコピー
データを分割し、各ワーカーごとに計算させる。

データ並列（同期型）

データ並列化は、各モデルのパラメータの合わせ方で同期型か非同期型か決まる。

各ワーカーの計算が終わるのを待ち、全ワーカーの勾配が出たところで勾配の平均を計算し、親モデルのパラメータを更新する。

データ並列（非同期型）

各ワーカーはお互いの計算を待たず、各子モデルごとに更新を行う。
学習が終わった子モデルはパラメータサーバーにプッシュされる。
新たに学習を始めるときは、パラメータサーバからポップしたモデルに対して学習していく。

同期型と非同期型の比較

処理スピードはお互いのワーカーの計算を待たない非同期型の方が速い。
非同期型は最新のモデルのパラメータを利用できないので、学習が不安定になりやすい。
現在は同期型の方が精度が良いことも多いので、こっちが主流。

モデル並列化

親モデルを各ワーカーに分割し、それぞれのモデルを学習させる。すべての学習が終わった後で、一つのモデルに復元。
モデルが大きい時はモデル並列化を、データが大きい時はデータ並列化をすると良い。

モデルのパラメータ数が多いほど、スピードアップしやすい。

GPUによる高速化

• GPGPU
  • 元々の使用目的であるグラフィック以外の用途で使用されるGPUの総称
• CPU
  • 高性能なコアが少数
  • 複雑で連続的な処理が得意
• GPU
  • 比較的低性能なコアが少数
  • 簡単な並列処理が得意
  • ニューラルネットの学習は単純な行列演算が多いので、高速化が可能

モデルの軽量化

モデルの精度を維持しつつ、パラメータや演算回数を低減する手法の総称。
特にモバイル端末やIoT機器など、一般的なパソコンに比べて演算性能が低い機器にAIモデルを搭載する際、計算の高速化と省メモリ化のために軽いモデルを作る必要がある。

モデル軽量化の方法としては、以下の3つ。
①量子化
②蒸留
③プルーニング

①量子化

ネットワークが大きくなると大量のパラメータが必要なり学習や推論に多くのメモリと演算処理が必要。
そこで通常のパラメータの64bit浮動小数点を32bitなど下位の精度に落とすことで、メモリと演算処理の削減を行う。

量子化は、計算の高速化・省メモリ化と精度の低下がトレードオフの関係にある。
64bitから32bit程度の量子化ではそこまで精度が変わらないとされているが、1bitなど極端に量子化をすると、誤差が大きくなってしまうので、ちょうどいい塩梅を考える必要がある。

②蒸留

精度の高いモデルの情報を軽量なモデルに落とし込めること。
一般に精度が高いモデルは、ニューロンの規模・パラメータ数が大きいモデルになっているので、推論にも多くのメモリと演算処理が必要。
そこで、規模の大きなモデルの知識を使って、軽量なモデルの作成を行う。
ここで、前者の規模の大きな、複雑なモデルのことを「教師モデル」、後者の作成するべき軽量なモデルを「生徒モデル」と呼ぶ。

③プルーニング

ネットワークが大きくなるにつれて、その分パラメータも大量になってくるが、実際全てのニューロンの計算が推測に役立っているわけではない。
そこで、モデルの精度の寄与が少ないニューロンを削除することで、モデルの軽量化・高速化をする方法。

実装演習

PyTorchで、データに複数のCPUコアを使用して並列アクセスすることで高速化を図る。ここではMNISTを使用する前提のもと、データに並列アクセスするDataLoaderを定義する。

import torch
import torchvision
import torchvision.transforms as transforms
import torch.nn as nn
import torch.nn.functional as F
import numpy as np

transform = transforms.Compose(
    [transforms.ToTensor(),
     ])
trainset = torchvision.datasets.MNIST(root='./data', train=True,
                                        download=True, transform=transform)

batch_size = 128

# num_workersでいくつのプロセスを使うか指定できる。
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch_size,
                                          shuffle=True, num_workers=6)

Section4 応用技術

MobileNet

ディープラーニングモデルは一般的に精度が良くなるが、モデル構造が複雑で、ネットワークが深くなるほど計算量が増えてしまう。
そのため、ディープラーニングモデルの軽量化・高速化・高精度化を実現するために提案されたネットワーク。
主に画像認識などに使われるモデルで、CNNの要素を盛り込んでいる。

基本概要は以下。

一般的な畳み込み層は計算量が多いが、MobileNetはDepthwise ConvolutiinとPointwise Convolutionの組み合わせで軽量化を実現している。

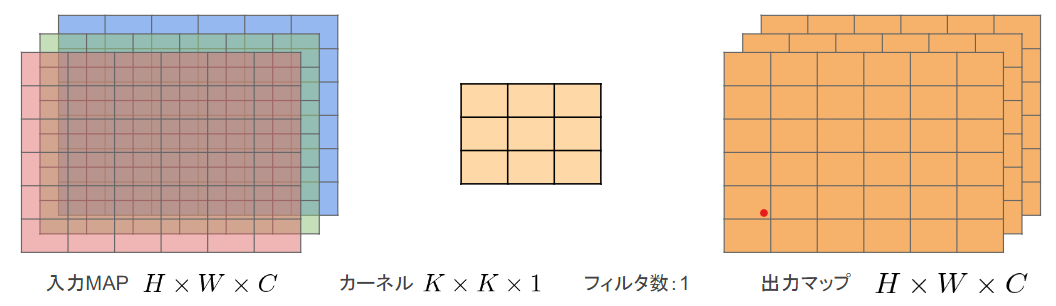
Depthwise Convolution

入力マップのチャネルごとに畳み込みを実施する構造。
出力マップをそれらと結合する。（よって、入力マップのチャネル数と同じになる）

通常の畳み込みでは、すべての層にかかっているので、これを使うと計算量が大幅に削減可能。
各層ごとの畳み込みであるので、層どうしの関係性は全く考慮されていない。
この点については、次のPointwise Convolutionと組み合わせることで解決している。

Pointwise Convolution

入力マップのポイントごとに畳み込みを実施する。
出力マップは、フィルタの数だけ作成可能（任意のサイズを指定できる）。

以上、これら2つの仕組みを合わせて、Depthwise Convolutionで空間方向に畳み込みを行ったうえで、Pointwise Convolutionでチャネル方向で畳み込みを行うことで、計算量を減らしつつ学習がちゃんと進むような仕組みになっている。

DenseNet

DenseNetはCNN系列のディープラーニングモデルの一つ。
一般的に層が深くなるほど学習が難しくなるという課題があったディープラーニングモデルに対して、前のブロックと直接接続させるResidual blockを導入することでパフォーマンスの向上を図ったモデルがResNetだった。
この発想を元に、各層の間で相互に接続するように構造を組めば、もっと精度が上がるのではないかという思想の下提案されたのがDenseNet。

実際のモデルの構造概要が以下。
全ての部分で相互に接続するのではなく、"DenseBlock"と呼ばれるひと塊のネットワーク内で相互に層を接続する。

この構造において、Dense Blockの間の畳み込み層・プーリング層で特徴マップのサイズを変更し、ダウンサンプリングを行っている。

DenseNetとResNetの違い

DenseBlockでは前方の各層からの出力全てが後方の層への入力として用いられる。
一方で、ResNetのResidual Blockでは、前1層の入力のみを後方の層へと入力する。

なお、DenseNet内で使用されるDenseBlockと呼ばれるモジュールでは、成長率と呼ばれるハイパーパラメータが存在している。

正規化技術

本編に出てきたBatchNormを始めとした正規化技術。

BatchNorm

層の間を流れているデータの分布を、ミニバッチごとに平均0、分散1になるように正規化。
BatchNormは、学習時間の短縮・過学習の抑制など、ニューラルネットワークモデルのパフォーマンス向上のためによく用いられる技術である。

LayerNorm

1データ内の各要素がすべて同一分布になるように正規化。
例えば、RGBの3チャンネルを持つデータの場合は、すべてのチャンネルの平均と分散を求めて、正規化を実施する。
特徴マップごとに正規化された特徴マップを出力。
こうすることで、ミニバッチの数に依存せずに正規化が可能。

InstanceNorm

それに加えてさらにチャンネルも同一分布に従うように正規化
各データ・各チャンネルごとに正規化。実質的にミニバッチサイズ1でBatchNormをするのと同じ。

WaveNet

一般的に画像処理に用いられることが多いCNNを音声に応用したもの。
時系列データに対する畳み込みで、層が深くなるにつれてリンクを離す。

深層学習を用いて結合確率を学習する際に、効率的に学習が行えるアーキテクチャを提案したことが、WaveNetの大きな貢献の一つ。

実装演習

（BatchNormは深層学習Day3 Section2の実装、LayerNormは深層学習Day4 Section5の実装に含まれる）