機械学習を勉強してみようと思って、ニューラルネットワークと深層学習というサイトを読んでいたら、わからない式が出てきました。
C(w,b)\equiv\frac{1}{2n}\sum_{x}\|y(x)-a\|^2
おうちの人に聞きながらがんばって解読したので、忘れないうちにメモしておきます。
##この式はなんなのか
コスト関数 という名前の関数です。ニューラルネットワークは、ひとつひとつのニューロンが複数の入力と1つの出力を持っていて、入力に対する重み付けを行うために重み(weight)を持っていて、さらに出力をどうするか決めるために、1つのしきい値(bias)を持っています。
ニューラルネットワーク全体の重みとしきい値をランダムで決めたときに、それらを使ってはじき出した人工知能の回答が、実際の答えとどれくらい離れているかを計測するために使う関数だと書いてありました。
この関数の値をゼロに近づけていくことが、ニューラルネットワークにとっての学習ということになるみたいです。
登場人物紹介
わからないところがいっぱいありますが、前後の文で説明されている記号はわかるので、それを先に書いておきます。
w:重み
C(\color{red}{w},b)\equiv\frac{1}{2n}\sum_{x}\|y(x)-a\|^2
重み(weight)のwです。各ニューロンの入力に対する重みなので、いっぱいあります。
b:しきい値
C(w,\color{red}{b})\equiv\frac{1}{2n}\sum_{x}\|y(x)-a\|^2
しきい値(bias)のbです。入力層を除くニューロンの数だけあります。
C(w,b):コスト関数
\color{red}{C(w,b)}\equiv\frac{1}{2n}\sum_{x}\|y(x)-a\|^2
コスト関数。パラメータにたくさんの重みとしきい値を取って、人工知能の出した答えがどれくらい現実の回答と離れているかを出す関数という感じです。これの定義が右辺にかかれているのだと思います。
x:入力データ
C(w,b)\equiv\frac{1}{2n}\sum_{x}\|y(\color{red}{x})-a\|^2
xは人工知能に渡す入力データです。本文では画像認識の例だったので、画像をバラバラにしてひとつひとつを点レベルに小さくして、その点の濃淡を数値で表したものの配列みたいな感じになります。
こういう「数値の集まり」のことを数学用語で ベクトル というらしいです。
y(x):人工知能が計算した結果
C(w,b)\equiv\frac{1}{2n}\sum_{x}\|\color{red}{y(x)}-a\|^2
y関数がニューラルネットワークにあたるものです。xという入力をとって、計算結果を返します。「重みとしきい値を設定したニューラルネットワークに、xという入力を与えた時の出力」を返す感じです。
本文の例では手書きの数字を判定しているのですが、判定結果は数値ではなく長さ10の配列になります。
[0,0,0,0,0,0,0,1,0,0] # 各要素が0〜9に対応している。この例では「7」を表す。
なのでこの結果もベクトルです。
a:期待される結果
C(w,b)\equiv\frac{1}{2n}\sum_{x}\|y(x)-\color{red}{a}\|^2
aはxという入力に対する本来の正解データです。人工知能が結果をベクトルで返すので、比較するためにこちらもベクトル形式です。
n:入力データの個数
C(w,b)\equiv\frac{1}{2\color{red}{n}}\sum_{x}\|y(x)-a\|^2
nは入力データの個数です。
いっぱいあってややこしい
いっぱいあるものがいっぱいあってわけがわからなくなってきました。実際の数字をあてはめて一旦整理してみます。
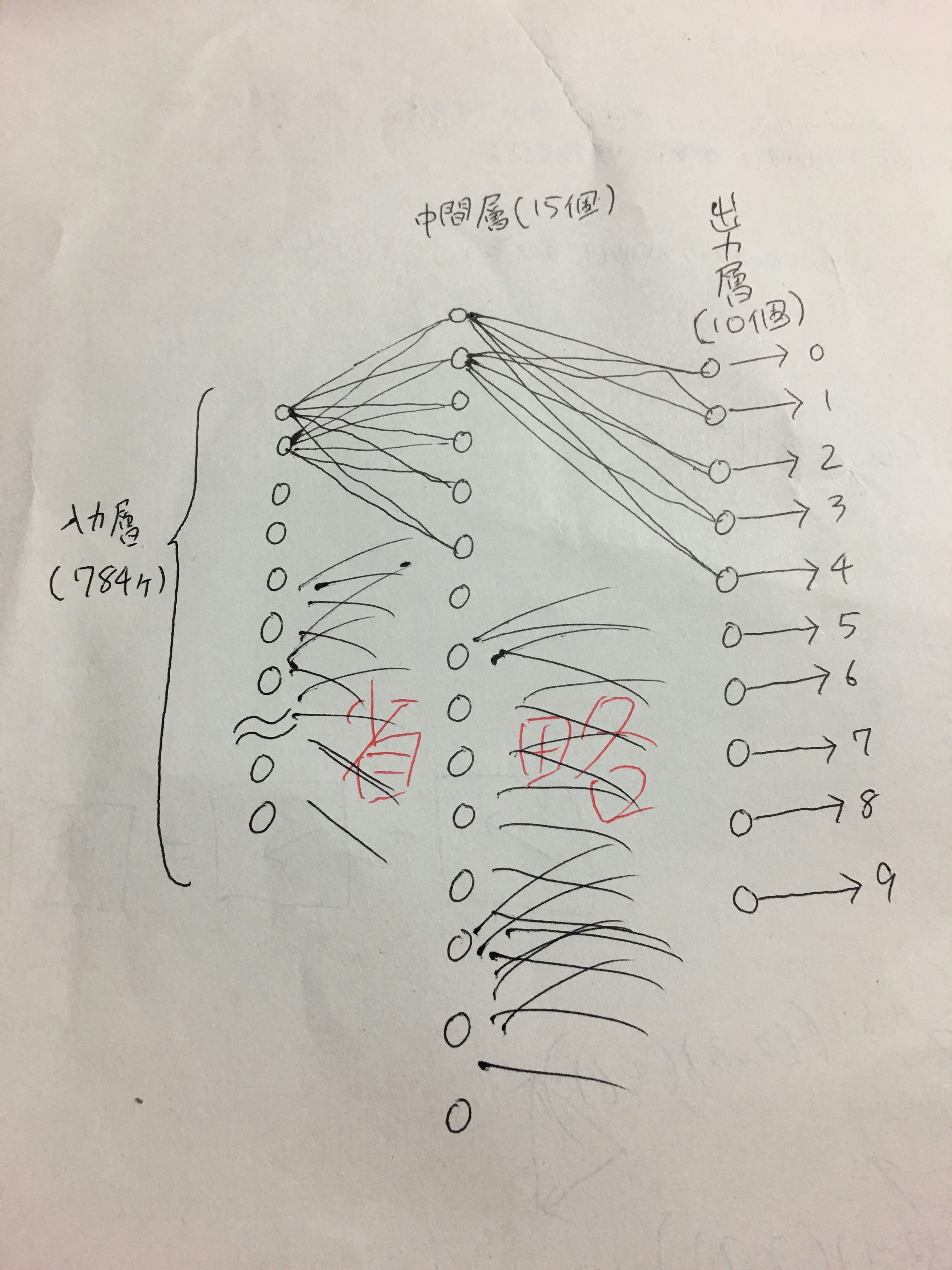
本文では手書きの画像を28×28のコマ切れ画像に分割してそれぞれの濃淡を数値にしたものを入力として人工知能に渡していました。なので入力データを表すxの要素数は28×28=784個です。
人工知能の出力は、長さが10のベクトルで、それぞれが0〜9の数に対応しているので、人工知能の回答を表すy(x)と正しい答えを表すaの要素数は10個です。
ニューラルネットワークの中身は、入力層が784個あって、中間層が15個、出力層が10個なので、重みは784×15+15×10=11,910個。しきい値は15+10=25個になります。
訓練用の手書き数字の画像データが60,000個あるので、n=60,000です。
また、xとy(x)とaはベクトルですが、このベクトルがそれぞれ訓練用データの数だけあります。xでいうと、要素数784個のベクトルが60,000個あるわけです。
いったんまとめ
ここまでわかったことを表にしてみます。なんとなく整理できてきました。
| 記号 | 意味 | ベクトルである | ベクトルの要素数 | ベクトルの数 |
|---|---|---|---|---|
| w | 重み | YES | 11,910個 | - |
| b | しきい値 | YES | 25個 | - |
| x | 入力データ | YES | 784個 | 60,000個 |
| y(x) | 人工知能の回答 | YES | 10個 | 60,000個 |
| a | 正しい答え | YES | 10個 | 60,000個 |
| n | 学習用データの数 | NO | - | - |
数式の方も、わかったところに色をつけてみます。分数の掛け算と2乗の計算は私でも分かったのでここも色をつけておきます。
\color{red}{C(w,b)}\equiv\color{red}{\frac{1}{2n}}\sum_{x}\|\color{red}{y(x)}-\color{red}{a}\|^\color{red}{2}
けっこう解読できてきました。ここから先がわからなくて、ググるのも困難だったので、数学に自信ニキに聞いて教えてもらいました。
三本線のイコール
C(w,b)\color{red}\equiv\frac{1}{2n}\sum_{x}\|y(x)-a\|^2
三本線のイコール≡は、中学校のときに習った記憶があって、「2つの図形が合同である」っていう意味だったはずなのですが、どうやら違うようです。
≡には複数の意味があって、その中の一つに 左辺を右辺の通り定義する というのがあります。この場合だと、「コスト関数の定義を右辺で説明しているよー」っていう意味なのだと思います。
ベクトルの引き算
C(w,b)\equiv\frac{1}{2n}\sum_{x}\|\color{red}{y(x)-a}\|^2
y(x)-aを計算しているので、人工知能の出した答えと期待される答えの差分を計算しているのだと思います。ただしy(x)もaも、要素数が10個のベクトルなので、引き算の結果は全ての要素が0のベクトルか、[0,0,1,0,0,0,0,-1,0,0]のように、どこかが1でどこかが-1のベクトルになります。
おそらくですが、ベクトルで引き算をすることによって、例えばホントは9なのに人工知能が0と判断した場合と、3を4だと間違えた場合を等価に扱えるようになってるんだと思います。
2本の縦線
C(w,b)\equiv\frac{1}{2n}\sum_{x}\color{red}\|{y(x)-a}\color{red}\|^2
2本の縦線は 距離関数 と呼ばれるものと本文では説明されています。この距離関数だけは調べてもよくわかりませんでした。
「ベクトルの距離ってなんだよ」っていう話なのですが、少なくともベクトルを数値に変換することができるというのは間違いないようです。
ベクトルの各要素を2乗して足し上げることでベクトルを数値に変換しているようです。今回の例だとy(x)とaが完全に一致していたら0になって、一致していなかったら1と-1が一個ずつあるので、計算結果は2になります。
Mが横向きになったやつ
C(w,b)\equiv\frac{1}{2n}\color{red}{\sum_{x}}\|{y(x)-a}\|^2
Σはシグマと読みます。日本語だと総和。ここの表記が省略されたものだったので非常に混乱しました。
「Σの右にあるものを全て足し算する」という意味の記号なのですが、ここでΣの下にあるxは、全ての入力データ(60,000個)を表していて、Σの右にあるxは一つ一つの入力データを表していたようです。
つまり、「60,000個ある入力データひとつひとつに対して、人工知能の出した答えと、期待される答えを比較して数値にして(0か2になる)、それを2乗したものを60,000個分全部足す」という計算をすることになります。
この計算結果に対してデータの個数(60,000個)×2で割り算をしているので、なんとなく平均を求めているんだなあというのが予想できます。計算の途中で2乗したり平均なのにデータの個数×2で割ってるのは何故なのかわかりませんでした。数学に自信ニキによると積分というのをしているのだそうです。積分と聞いた瞬間ひどいめまいと吐き気に襲われたので今日はこの辺にしておいてやろうと思いました。
まとめ
C(w,b)\equiv\frac{1}{2n}\sum_{x}\|{y(x)-a}\|^2
コスト関数は、たくさんの教育用入力データに対して、人工知能が出した答えと本来の正解の差分を計算して、それの平均を取ると定義される。コスト関数は人工知能の誤差を定量化することを目的とした関数である。コスト関数は、ニューラルネットワークに設定するたくさんの重みとたくさんのしきい値をパラメータにとって、人工知能の誤差を数値として返す関数である。
このコスト関数の返す値を最小化するように、パラメータの重みとしきい値を調整していくことが必要で、この工程が人工知能が学習すると呼ばれているのだと思います。
感想
数学に強い人だとスラスラ読めたり、少しくらいわからなくてもニュアンスでなんとかなるのでしょうが、数学に自信のない人間がいきなり
\sum
みたいな読み方もわからない記号を見るとびっくりしてやる気がなくなってしまいます。
ただ、数式もひとつひとつ分解して調べたら何とか理解できたし、何が書いてあるのか全くわからなかったものが読めるようになるのは楽しいです。こうやって一回じっくり調べながら読んでみると、次に似たような数式に出会っても驚かなくて済むよと言われたので、この調子で読み進めてみようと思います。