この記事は高知工科大学AdventCalender2017の20日目の記事です。
モーションデブラーとは
写真撮るときに、カメラや対象が動いた時におこるブレを取り除くこと。
で、本題に入る前に（ご存知かもしれませんが）ブレの発生について少し説明したいと思います。
ブレの発生
写真を撮る時、カメラはある程度の時間の光を集めて加算していき出力します。
この時間中に対象が動くと、異なる信号が加算されていくためブレが発生します。
簡単化のため等速直線運動を考え、運動方向をu軸にとってモデル化すると、
$$ b(u, v) = \int_{-T/2}^{T/2} x(u-Vt, v)~dt + n(u, v) $$
- $b$ : ブレが発生している画像
- $T$ : 露光時間
- $x$ : 入力信号の関数
- $V$ : 移動速度
- $n$ : ノイズ
となりますが、ディジタル画像は関数ではなくピクセルとして表現される離散値であるため、行列・ベクトル方程式で近似できます。
$$ \boldsymbol{b} = A \boldsymbol{x} + \boldsymbol{n} $$
と言われても... という感じかもしれない（であってほしい）ので、1次元の信号でちょっと考えたいと思います。
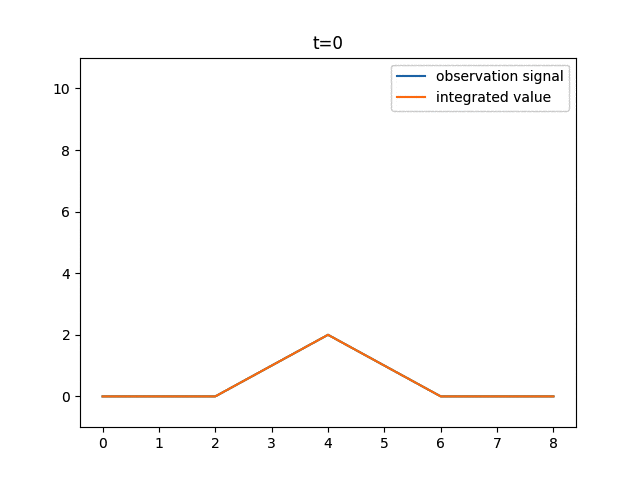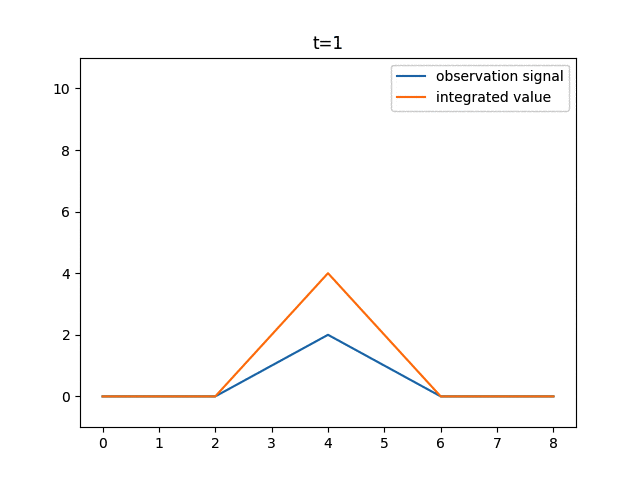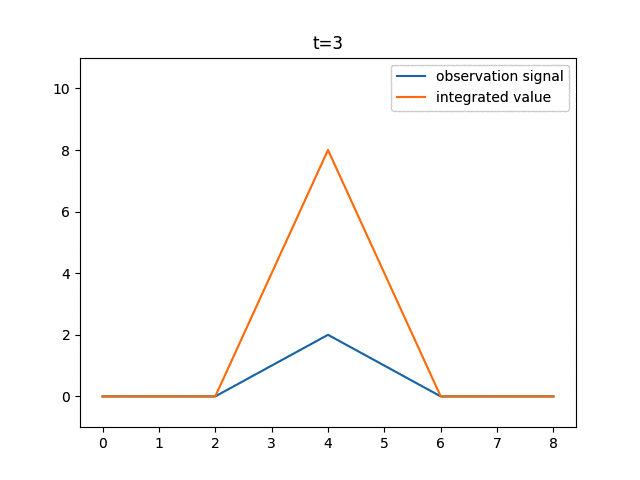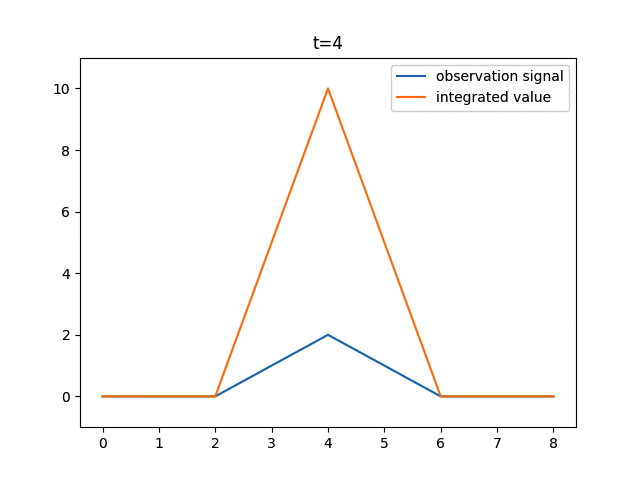
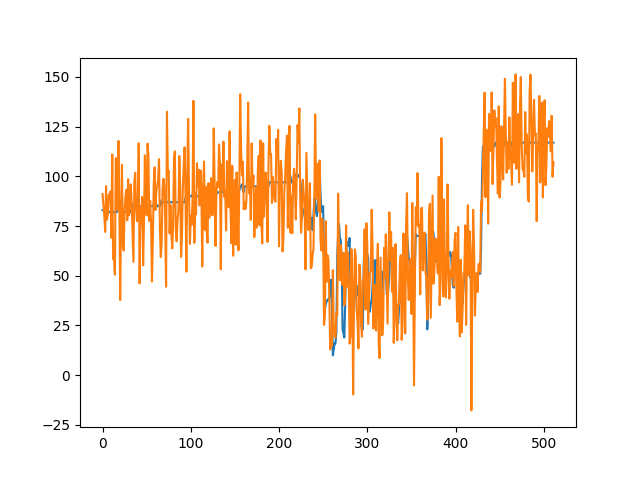
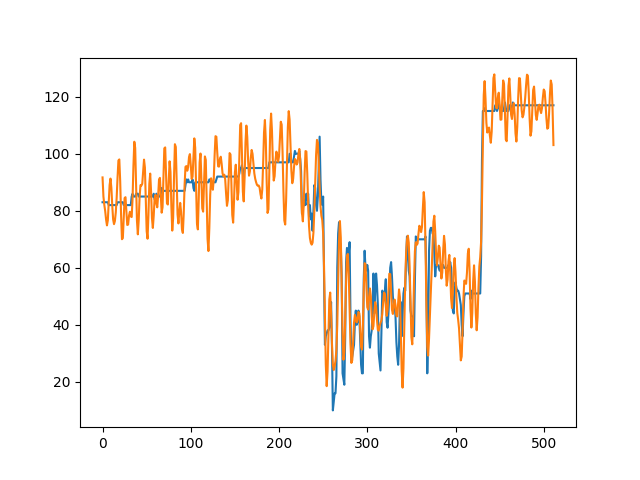
10ピクセルの信号に対して、静止している場合と1ピクセルずつ動いた場合に得られる積分値を表示してみます。
静止
移動
上図では、信号x=[0, 0, 0, 1, 2, 1, 0, 0, 0]が右に1ずつシフトしています。
この時得られる積分値の5番目の値b[4]は、次のように計算することができます。
b[4] = x[4-(-2)] + x[4-(-1)] + x[4-0] + x[4-1] + x[4-2]
= x[6] + x[5] + x[4] + x[3] + x[2]
= 0 + 1 + 2 + 1 + 0
= 4
ということは...
線形代数でブレを考える
考え方
上記で示した配列のような計算を方程式で（っぽく？）書くと、
$$b_5 = x_3 + x_4 + x_5 + x_6 + x_7 $$
ここで、$b_2$はどうなるかちょっと考えると、もともと画像内に無い値$w$が出てくる。
$$ b_2 = w + x_1 + x_2 + x_3 + x_4 $$
$w$どうするの？っていうことで
- 0
- $x_1$ (反射）
- $x_n$ (周期）
を考えるといいらしい。今回は周期性を持たせた$x_n$を採用する。（離散フーリエ変換が周期性を仮定しており、パワースペクトルが綺麗になるため）
ということで、まとめると、
\left\{
\begin{matrix}
b_1 & = & x_1 & + & x_2 & + & x_3 & & & & & & & & & + & x_8 & + & x_9 \\
b_2 & = & x_1 & + & x_2 & + & x_3 & + & x_4 & & & & & & & & & + & x_9 \\
b_3 & = & x_1 & + & x_2 & + & x_3 & + & x_4 & + & x_5 & & & & & & & & \\
b_4 & = & & & x_2 & + & x_3 & + & x_4 & + & x_5 & + & x_6 & & & & & & \\
b_5 & = & & & & & x_3 & + & x_4 & + & x_5 & + & x_6 & + & x_7 & & & & \\
b_6 & = & & & & & & & x_4 & + & x_5 & + & x_6 & + & x_7 & + & x_8 & & \\
b_7 & = & & & & & & & & & x_5 & + & x_6 & + & x_7 & + & x_8 & + & x_9 \\
b_8 & = & x_1 & & & & & & & & & + & x_6 & + & x_7 & + & x_8 & + & x_9 \\
b_9 & = & x_1 & + & x_2 & & & & & & & & & + & x_7 & + & x_8 & + & x_9 \\
\end{matrix}
\right.
行列計算にすると、
\begin{bmatrix}
b_1 \\ b_2 \\ b_3 \\ b_4 \\ b_5 \\ b_6\\ b_7 \\ b_8 \\ b_9
\end{bmatrix}
=
\begin{bmatrix}
1 & 1 & 1 & & & & & 1 & 1 \\
1 & 1 & 1 & 1 & & & & & 1 \\
1 & 1 & 1 & 1 & 1 & & & & \\
& 1 & 1 & 1 & 1 & 1 & & & \\
& & 1 & 1 & 1 & 1 & 1 & & \\
& & & 1 & 1 & 1 & 1 & 1 & \\
& & & & 1 & 1 & 1 & 1 & 1 \\
1 & & & & & 1 & 1 & 1 & 1 \\
1 & 1 & & & & & 1 & 1 & 1 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ x_7 \\ x_8 \\ x_9
\end{bmatrix}
つまり、
$$ \boldsymbol{b} = A \boldsymbol{x} $$
よって、
$$ \boldsymbol{x} = A^{-1} \boldsymbol{b}$$
とすると、ブレた画像から綺麗な画像が作れるという感じです。
実験（ノイズなしver.）
実際に画像を使ってどこまでできるか確認してみます（やっとコードが）。
ブレ画像の作成
import numpy as np # 行列計算に使うよ
from scipy misc, signal # 使用画像準備/保存, 畳み込み演算 に使うよ
d = 31 # 移動距離
img = misc.ascent() # 使用する画像
bimg = blur(img, d) # モーションブラー（関数の中身は後述）
blur関数の内容は下（とりあえず横方向のブレだけ）
def blur(img, d):
fil = np.zeros((d, d))
fil[d//2, :] = 1/d
return signal.convolve2d(img, fil, mode='same', boundary='wrap')
使用した原画像とブラー画像はこんな感じ。
原画像
ブラー画像
行列Aの作成とデブラー
まず、行列$A$を作成します。
H, W = img.shape[:2]
A = np.zeros((W, W)):
for i in range(W):
for j in range(d):
k = (i - d//2 + j) % W
A[i, k] = 1/d
A = np.matrix(A)
今回は横方向の移動を扱うので、ベクトル$\boldsymbol{b}$は画像の任意の行になります。
とりあえず、0行目で計算してみる。
N = 0
b = np.matrix(bimg[N, :]).T # 0行目の取得と列ベクトル化
A_inv = A.I # 行列Aの逆行列を取得
x_hat = A_inv * b # 元画像の推定
完全一致！（当たり前）
全行に対して処理を行って画像を復元した結果を見て見ます。
超綺麗！すごーーい！（当たり前）
ちょろそうなので、ちょっとノイズ足してみます。
noise = np.random(H, W) * np.average(bimg) * 0.05
noise -= noise.max()/2
nbimg = bimg + noise
ノイズを足した画像
で、同様に復元します。
0行目
復元画像
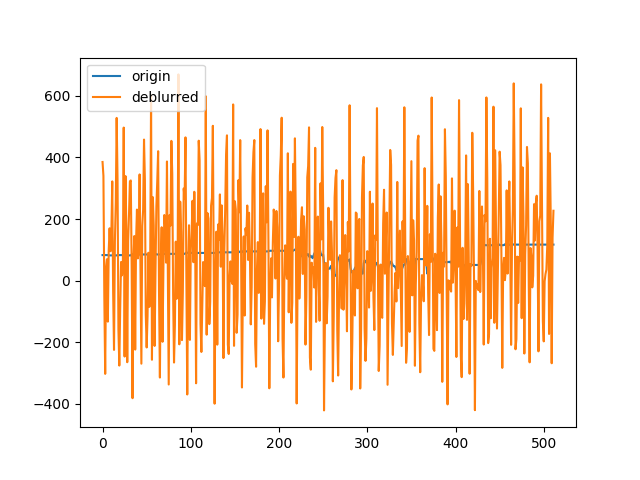
......何......だと......
SVD（特異値分解）の利用
SVDは行列Aを次にように分解します。
$$ A = U\Sigma V^T $$
- $\Sigma = \rm{diag}(\sigma_1, \sigma_2, ..., \sigma_n),~~~\sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_n \ge 0 $ （特異値の対角行列）
- $U^TU = I$, $V^TV=I$（転置が逆行列）
これを復元の式に適用すると、
\begin{align}
\boldsymbol{x} &= A^{-1} \boldsymbol{b} \\
&=(U \Sigma V^T)^{-1} \boldsymbol{b} \\
&= V\Sigma^{-1}U^T \boldsymbol{b} \\
&= \sum_{i=1}^n \frac{\boldsymbol{u}_i^T\boldsymbol{b}}{\sigma_i}\boldsymbol{v}_i
\end{align}
小さな特異値の影響をフィルタ$\phi_i$によって除外し、復元結果をよくしてみる。
（特異値$\sigma_i$の除算によってエラーが大きくなるのを防ぐためだと思います。間違っていたらすいません。よく調べておきます）
\boldsymbol{x}_{reg} = \sum_{i=1}^n \phi_i \frac{\boldsymbol{u}_i^T\boldsymbol{b}}{\sigma_i}\boldsymbol{v}_i
\phi_i \approx \left\{ \begin{align}
1~~~~~& \rm{if}~\sigma_i~is~large \\
0~~~~~& \rm{if}~\sigma_i~is~small
\end{align} \right.
$\phi_i$をとりあえず2つ。
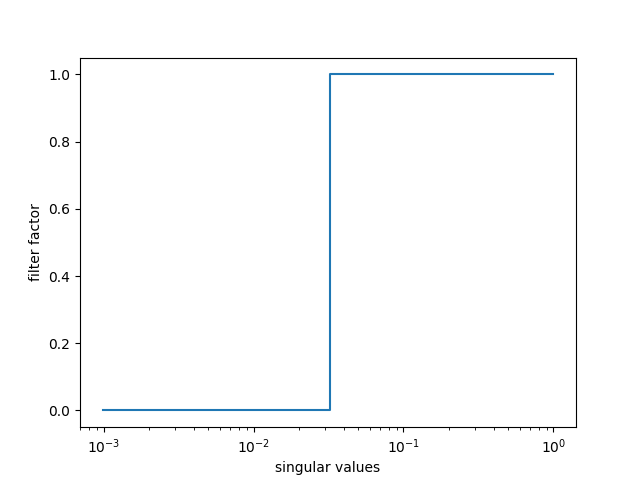
- Truncated SVD
\boldsymbol{x}_{tsvd} = \sum_{i=1}^k \frac{\boldsymbol{u}_i^T\boldsymbol{b}}{\sigma_i}\boldsymbol{v}_i
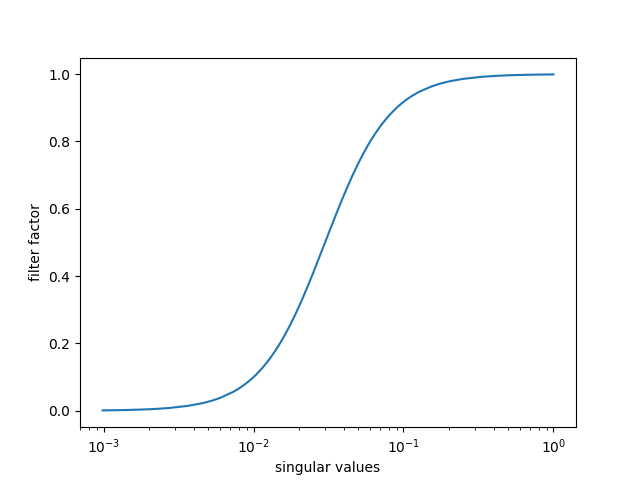
- Tikhonov
\boldsymbol{x}_{tsvd} = \sum_{i=1}^n
\frac{\sigma_i^2}{\sigma_i^2+\alpha^2}
\frac{\boldsymbol{u}_i^T\boldsymbol{b}}{\sigma_i}\boldsymbol{v}_i
実験（SVD, ノイズありver.）
とりあえずSVDと$\phi$の定義
U, S, V = np.linalg.svd(A, full_matrices=True) # SVD
phi_tsvd = lambda i, k: int(i < k) # Truncated SVD
phi_tik = lambda s, a: s**2 / (s**2 + a**2) # Tikhonov
Truncated SVDで0行目の計算。kはとりあえず真ん中にしてみる。
k = W//2
x_tsvd = np.matrix(np.zeros(len(S))).T
for i, s in enumerate(S):
tmp = (U[:, i].T * b)[0,0] * V.T[:, i] / S[i]
x_tsvd += tmp * phi_tsvd(i, k)
結果
復元画像
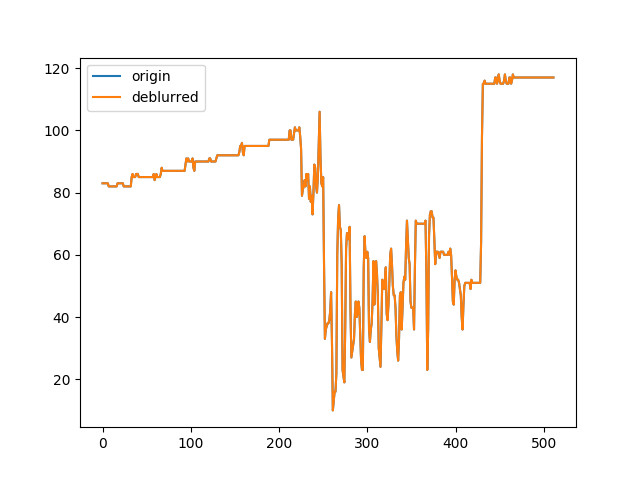
ノイズの影響はまだあるが、単純な逆行列よりかなり良くなったと思います！
最適パラメータ探索
せっかくなので、Truncated SVDでどのパラメータが最適なのか、原画像とのエラー（２乗距離の平均）から探索してみる。
$k=133$が今回の場合良かったらしい。
0行目
復元画像
参考資料
おわりに
とても拙い文章だったと思いますが、記事読んでいただきありがとうございます。