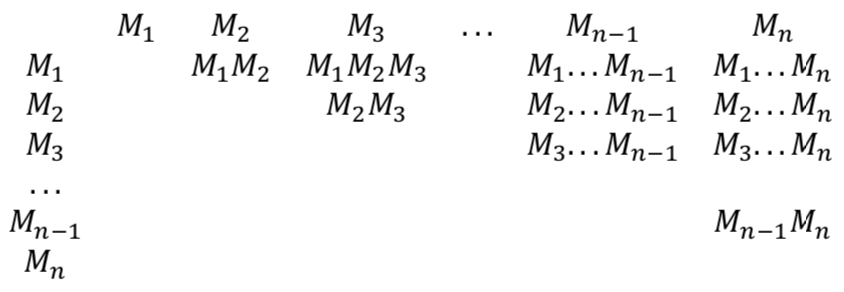連鎖行列積問題とは
- 行列連鎖積問題とは、行列を乗算するとき、使用される乗算の総数が最小になる乗算の順序を見つけることです。
- 行列連鎖積問題の解決策を見つけるために動的計画法を使用します。
-> 動的計画法とは
𝒍×𝒎行列𝑨と𝒎×𝒒行列𝑩が与えられる時、積𝑪は 𝒍×𝒒 行列です。
式から、𝑪の計算に使用される乗算数は、 𝑙×𝑚×𝑞 になります。
(𝒍 × 𝒒) (𝒍 × 𝒎) (𝒎 × 𝒒)
𝑪 = 𝑨 × 𝑩
𝑪[𝑖, 𝑗] = ∑(k=1→m)𝑨[𝑖, 𝑘] × 𝑩[𝑘, 𝑗]
ここで、次の行列の連鎖𝑴𝟏,𝑴𝟐,...𝑴𝒏(1 ≤ 𝑖 ≤ 𝑛 )の積𝑴を考えます。
(𝑟1 ×𝑟2) (𝑟2 ×𝑟3) (𝑟3 ×𝑟4) ... (𝑟𝑛−1 ×𝑟𝑛) (𝑟𝑛 ×𝑟𝑛+1)
𝑴𝟏 𝑴𝟐 𝑴𝟑 ... 𝑴𝒏−𝟏 𝑴𝒏
𝒏行列が一緒に乗算されることとします。
各行列は𝑟𝑖行と𝑟(𝒊+1)列を持つので、𝑴𝒊×𝑴(𝒊+1)の乗算数は、𝑟𝑖×𝑟(𝑖+1)×𝑟(𝑖+2)になります。
(𝑟𝑖 × 𝑟(𝑖+1)) (𝑟(𝑖+1) × 𝑟(𝑖+2))
𝑴𝒊 × 𝑴(𝒊+1)
積𝑴はさまざまな順序で計算できます。
例えば、𝑛 = 4のとき、 M1, M2, M3, M4 = A(𝟒×𝟐), B(𝟐×𝟑), C(𝟑×𝟏), D(𝟏×𝟐) とすると
1. (((A×B)×C)×D)
2. (A×((B×C)×D))
3. ((A×B)×(C×D))
4. ((A×(B×C))×D)
5. (A×(B×(C×D)))
の5通りの順序があります。
1と5の乗算数を比較すると、
1. ((A×B)×C)×D)=4×1×2=8、 5. (A×(B×(C×D)))=4×2×2=16
このように、計算に順序によって計算回数が変わることが分かります。
アルゴリズム
- 𝑴𝟏𝑴𝟐, 𝑴𝟐𝑴𝟑, ... の乗算数は 𝒓𝟏 × 𝒓𝟐 × 𝒓𝟑, 𝒓𝟐 × 𝒓𝟑 × 𝒓𝟒, ...のように一つしか存在しません。
- これらのコスト（乗算の回数）をテーブルに格納します。
- 連続した3つ(𝑀1𝑀2𝑀3 , 𝑀2𝑀3𝑀4 ,..., 𝑀𝑛−2𝑀𝑛−1𝑀𝑛)を乗算するための最良の方法を見つけます。
例）𝑀1𝑀2𝑀3の最小コストは、次のどちらかになります。
1. 𝑀1𝑀2𝑀3 = 𝑀1𝑀2のコスト + (𝒓𝟏×𝒓𝟑×𝒓𝟒)
2. 𝑀1𝑀2𝑀3 = 𝑀2𝑀3のコスト + (𝒓𝟏 ×𝒓𝟐 ×𝒓𝟒)
((𝑀1𝑀2)𝑀3)と(𝑀1(𝑀2𝑀3))のコストを求めるとき、(𝑀1𝑀2)と(𝑀2𝑀3)のコストを再計算するのではなく、テーブルから見つけるようにします。
- (𝑀1𝑀2𝑀3 , 𝑀2𝑀3𝑀4 ,..., 𝑀𝑛−2𝑀𝑛−1𝑀𝑛)の最小コストをテーブルに格納します。
この段階でのテーブル
- このように、 (𝑀𝑖𝑀𝑖+1 ...𝑀𝑖+𝑗)のコストを求めるときは、(𝑀𝑖𝑀𝑖+1...𝑀𝑘−1)と(𝑀𝑘...𝑀𝑖+𝑗)の最小コストをテーブルから見つけることでコスト（𝑟𝑖 × 𝑟𝑘 × 𝑟(𝑖+𝑗+1)）を求められます。
- (𝑀𝑖𝑀𝑖+1 ...𝑀𝑖+𝑗)の最小コストをテーブルに格納します。
- これを繰り返します。
擬似コード
def MATRIX_CHAIN_ORDER(r):
# r - 行列のリスト
# m - コストのテーブル, s – 最適なコストの指標となるテーブル
n = r.length - 1
m = matrix(1...n, 1...n)
s = matrix(1...n - 1, 2...n)
for i = 1 to n:
m[i, i] = 0
for l = 2 to n:
for i = 1 to n – l + 1:
j = i + l–1
m[i, j] = ∞
for k = i to j – 1:
q = m[i, k] + m[k + 1, j] + ri - 1rkrj
if q < m[i, j]:
m[i, j] = q
s[i, j] = k
return m, s
# 計算の順序を見る為に、最適な括弧を表示する
def PRINT_OPTIMAL_PARENS(s, i, j):
# 与えられたsから、最適な括弧を出力する
if i == j:
print "A"(i)
else:
print "("
PRINT_OPTIMAL_PARENS(s, i, s[i, j])
PRINT_OPTIMAL_PARENS(s, s[i, j] + 1, j)
print ")"
実装
以下参照
- Matrix chain multiplication