ハフマン符号とは
1952年にデビッド・ハフマンによって開発された符号で、文字列をはじめとするデータの可逆圧縮などに使用される。
よく出現する文字には短いビット列を、あまり出現しない文字には長いビット列を割り当てることで、メッセージ全体の符号化に使われるデータ量を削減することを狙っている。
Wikipediaより
可変長符号の一つ。 -> 可変長符号とは
アルゴリズム
与えられた文字列に含まれている文字の集合をSとする。
Sに含まれる各文字の頻度を数える。
Sを二分木の根の集合として考える。各木は1つのノードを持つ。
最小の頻度の文字2つを見つけ、2つの根として新しいノードを生成する。
新しい根は、2つの子の出現頻度の合計の出現頻度を持つ。
Sから2つの文字を削除し、Sに新しい根を追加します。
Sの長さが1になるまで、2の手順を繰り返す。
擬似コード
def HUFFMAN (S):
# Input: S 属性freq(頻度)を持つn個の文字のセット。freqはQのための鍵になる。
n = |S| # Sの長さ
Q = MIN_PRIORITY_QUEUE(S)
for i = 1 to n -1:
allocate new node z
z.left = x = EXTRACT_MIN(Q)
z.right = y = EXTRACT_MIN(Q)
z.freq = x.freq + y.freq
INSERT(Q, z)
return EXTRACT_MIN(Q)
実装
from collections import Counter
def MIN_PRIORITY_QUEUE(S):
return sorted(S.items(), key=lambda x: x[1], reverse=True)
def EXTRACT_MIN(Q):
return Q.pop()
def INSERT(Q, z):
return Q.append(z)
def HUFFMAN(S, a):
n = len(S)
Q = MIN_PRIORITY_QUEUE(S)
for i in range(n - 1):
left = EXTRACT_MIN(Q)
right = EXTRACT_MIN(Q)
freq = left[1] + right[1]
z = (left[0] + right[0], freq)
INSERT(Q, z)
a.append([left, "0", left[0] + right[0]])
a.append([right, "1", left[0] + right[0]])
Q = dict(zip([i[0] for i in Q], [i[1] for i in Q]))
Q = MIN_PRIORITY_QUEUE(Q)
a.append([EXTRACT_MIN(Q), "", "top"])
return a
def PrintReslut(b):
for i in range(len(a)):
now = a[i][0][0]
num = a[i][1]
j = 0
while a[j][2] != 'top':
if a[i][2] == a[j][0][0]:
num = a[j][1] + num
i = j
flag = 0
for k in range(len(a)):
if a[k][0][0] == 'top' or a[j][2] == a[k][0][0]:
flag = 1
break
else:
j += 1
if now in s:
b.append([now, num])
return b
def DivideS(S):
S = list(S)
S = Counter(S)
S = dict(S)
return S
s = DivideS(input())
a = HUFFMAN(s, [])
for b in sorted(PrintReslut([])):
print(b[0] + ": " + b[1])
例
文字列: ABBCACCEACBCCFABCDAFEABFFADBBC
S = {"A": 7, "B": 7, "C": 8, "D": 2, "E": 2, "F": 4}
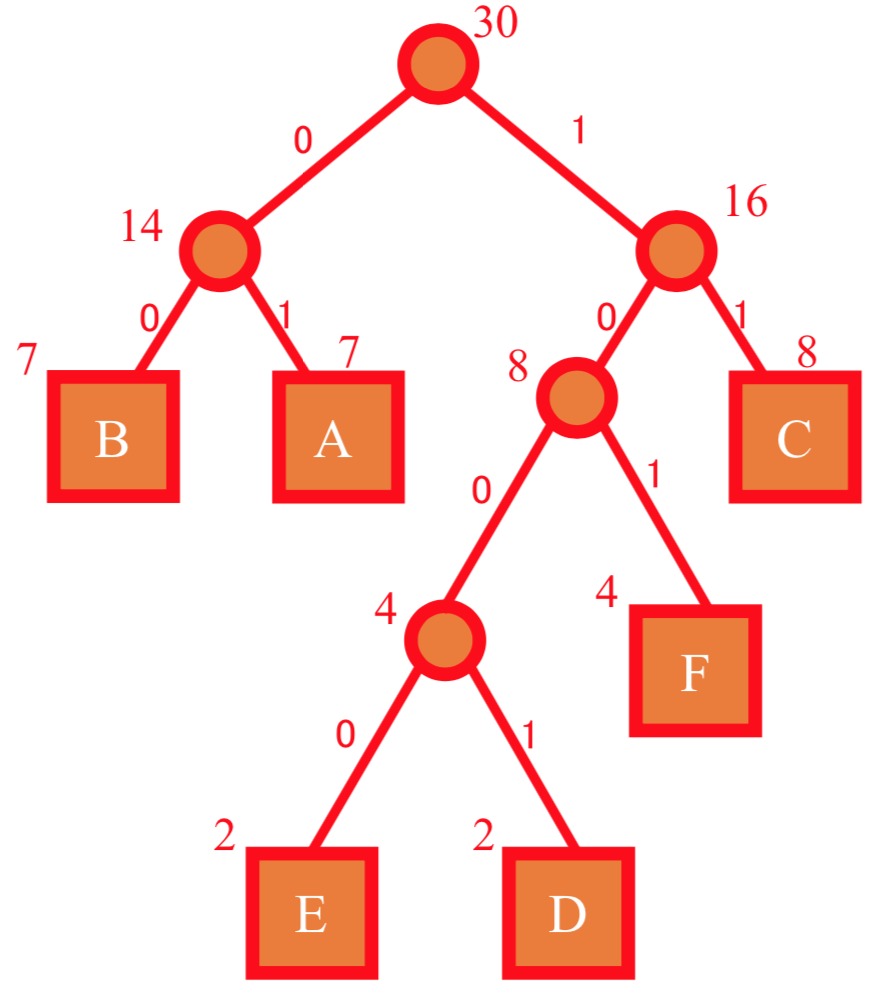
A: 01
B: 00
C: 11
D: 1001
E: 1000
F: 101
デコード
文字列内の最初のビットから始めて、文字列からの連続するビットを使用して、デコードツリー内を左に移動するか右に移動するかを決定する。
ツリーのリーフ(文字)に到達したら、その文字を出力(デコード)用の文字列に追加する。
※ 圧縮ファイルにはコード表が含まれていなければならない。