小売業における数理最適化事例

はじめに

TRIAL＆RetailAI Advent Calendar 2024 の 2日目の記事です。

昨日は @rockmetoou さんの『Safely sync database cluster to a standalone database for local usage』という記事でした。

運用上の負担軽減いい感じですね🙌

本日は、『小売業における数理最適化事例』 です
小売業での応用事例のイメージが少しでも伝わればと思っております🙇

数理最適化とは？

数理最適化は、最適な資源配分を行う数学的手法です

• 限られた資源を効率的に使い、最大の効果を引き出します
• 企業経営や交通、エネルギー管理などで活用されています
• 線形計画法や整数計画法などの具体的な手法があります

図引用：ORを探せ！

達成したいイメージ

『 ある数量の、ある商品を、特定の期間で、店舗ごとの規模感や、季節性(需要)などを加味して店舗別に配分したい 』

モチベーション ⇨ 多くの必要としている方にできるだけ行き渡るようにしたい💪

お題

『 合計「1,000個」のある商品「〇〇〇」を「5期間」に「5店舗」で、いい感じに配分する 』

設定

• ある商品：架空の１商品(「〇〇〇」)
• 合計数量：1,000個
• 特定の期間：5期間
• 店舗数：5店舗
  • large：1店舗
  • middle：3店舗(middle1，middle2，middle3)
  • small：1店舗
• 規模感
  • large：middleの2倍の需要
  • small：middleの0.5倍の需要
• 季節性(需要)：以下の図にある３パターン
  • 各店舗は、以下のパターンで売れていくとする
    • pt1：large，middle1，small
    • pt2：middle2
    • pt3：middle3

条件：期間ごとの最大需要数

今回、各フォーマットごとの各期間における需要数の上限値は以下のものとする

• middle
  • 期間1,2,3,4,5 ＝　[100, 50, 50, 50, 20]
    • 期間1の最大需要数：100個、期間2の最大需要数：50個、...
• large：middleの2倍の需要
  • 期間1,2,3,4,5 ＝　[200, 100, 100, 100, 40]
• small：middleの0.5倍の需要
  • 期間1,2,3,4,5 ＝　[50, 25, 25, 25, 10]

アプローチ：凸二次計画問題

凸二次計画問題は、目的関数が二次関数で制約条件が線形の最適化問題です

• 目的は、与えられた制約の中でこの二次関数の値を最小化または最大化することです
• この問題は、ポートフォリオ最適化や機械学習など多くの分野で応用されます
• 効率的なアルゴリズムが存在し、数理的に解きやすい特徴があります

最適化結果

以下の3つの条件を元に最適化します

• 需要(パターン)
• 各期間の最大需要数(例：middle⇨[100, 50, 50, 50, 20])
• 全体の数量(= 1,000個)

最適化結果

• それぞれのフォーマットで各期間の最大需要数を超えることがないです
• パターンと同じイメージの配分になっています
• 5店舗、5期間の合計が1,000個になっています

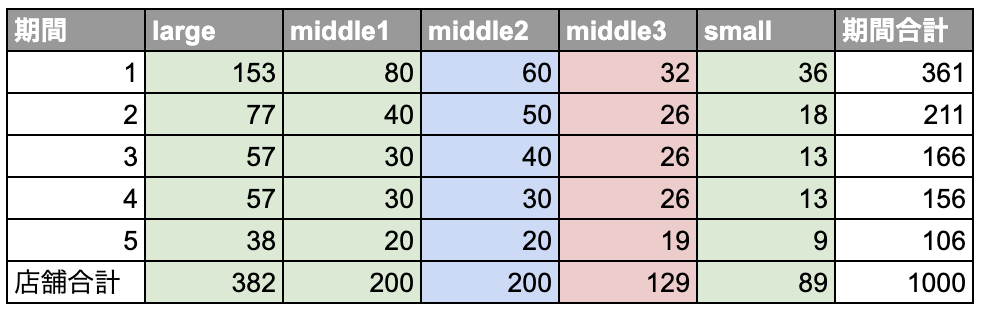
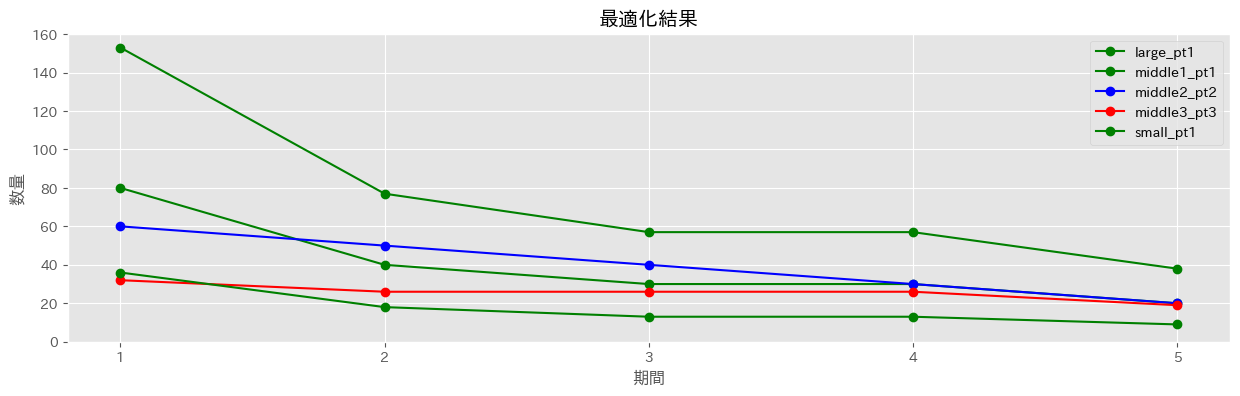
最適化結果の個人的な解釈

• largeがmiddle1,middle2の約2倍、smallの約4倍の配分になっていて、いい感じです
• middle3が全体で129個であり、まだ配分出来そうなので合計数量はもう少し多くても良さそうです
  • わかりやすく1,000個にしてみました⇨この条件なら1,100個でも良さそうです

まとめ

実務では、様々な制約に悪戦苦闘しながら日々頑張っています💪

明日は、@yang_zaiqiさんの「俺のAndroid™ スマートフォンで大規模言語AIモデルを動かせるの？」という記事です。お楽しみに！

RetailAIとTRIALではエンジニアを募集しています。
興味がある方はご連絡ください！

参考文献

• しっかり学ぶ数理最適化

• Pythonではじめる数理最適化（第2版）