リアルなサイトのスピード
PageSpeed Insightsの実際のユーザーの環境で評価するの欄を見ると、そのページやサイトが実際に(Chromeブラウザに限りますが)どのくらいのスピードで体験された、おおよその割合でわかります。

ビューを開くを押すとさらに詳細見ることができます。例えばapple.com全体のLCPはこんな感じで、2.5秒以内のPVが61%、4秒以上のPVが18%です(2023年12月12日時点)。
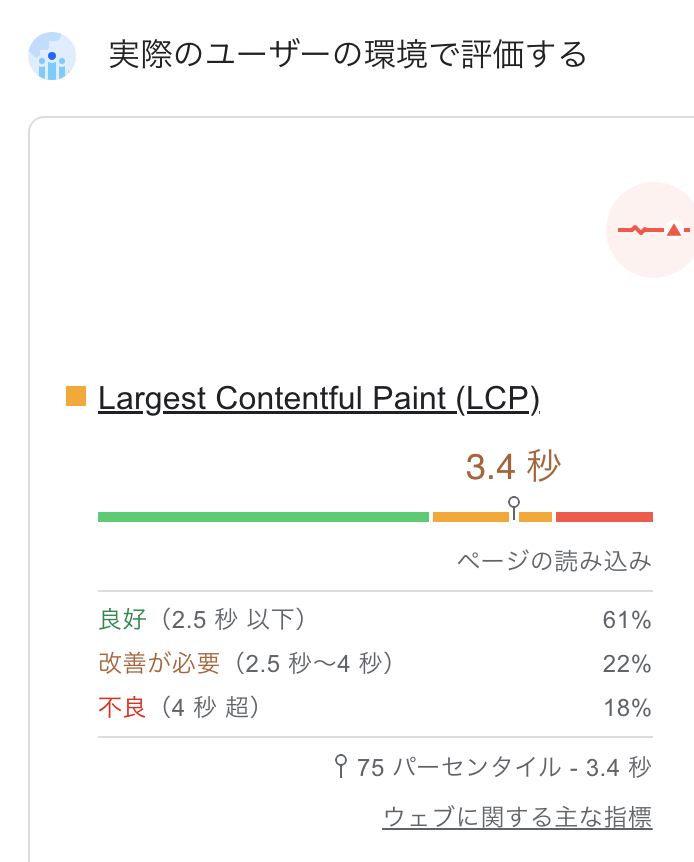
なんとなく緑が大きいといいのはわかるんですが、具体的にどのくらいのスピードなのか感覚的なものとしてピンとこないと思いませんか?
この割合からもっと具体的な分布を想像する、ということを試したところ、案外うまく行ったので方法を紹介します。
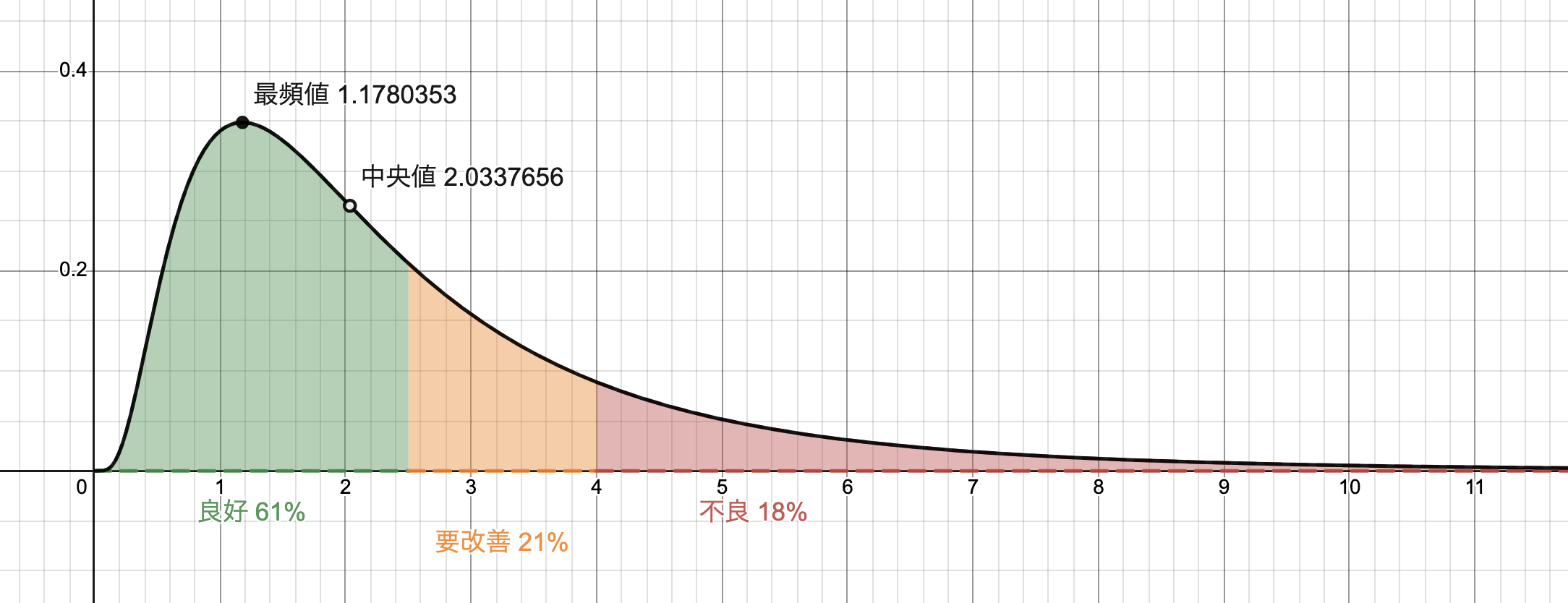
このグラフだと、LCPは1.18秒くらいになる可能性が一番高いということがわかりました。これだと感覚的な数値として想像しやすいです。
対数正規分布
Webのスピードに関する指標は対数正規分布に従うとされます。
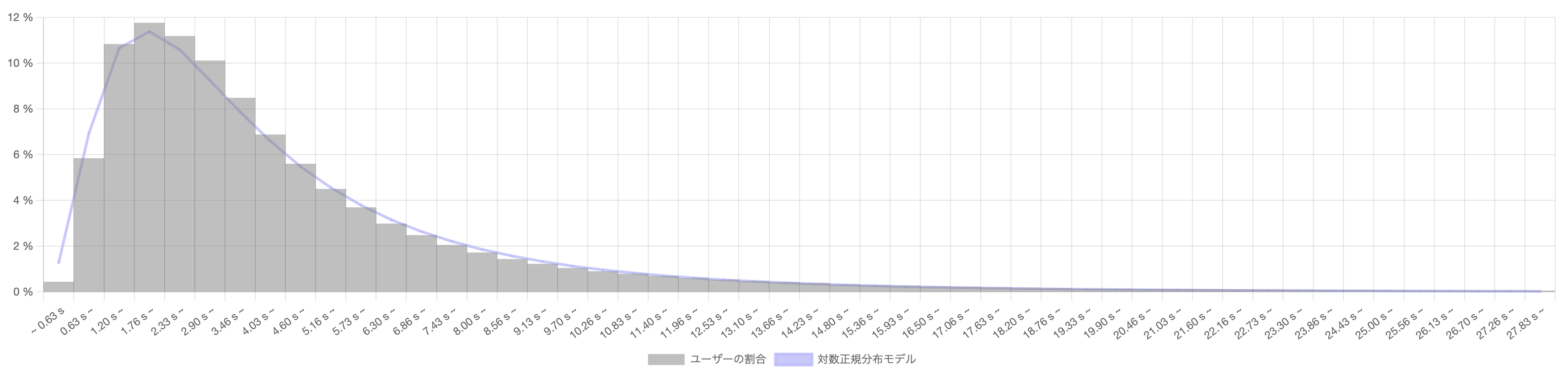
以下は実際にあるサイトで読み込み時間(OnLoad)を測定した結果です。計測値のヒストグラムと、中央値と平均値から対数正規分布を計算して薄い線で重ねたものですが、
ヒストグラムと理論的な予想が驚くほど一致していることがわかります。
他にもPageSpeed Insightsの内部でスコアの計算に対数正規分布が用いられています。
対数正規分布のパラメータ
対数正規分布のパラメータはμとσのふたつです。
データとして、
- 2.5秒以下の累積度数が61%
- 4秒以下の累積度数が100-18=82%
というヒントが得られているので、これらからμとσを求めてみます。
まず、対数正規分布の累積度数分布関数がこちらですが、
f\left(x\right)=\frac{1}{2}\left(1-\operatorname{erf}\left(-\frac{\ln\left(x\right)-μ}{\sqrt{2}σ}\right)\right)
これをμとσについての式に変形するとこんなふうになりました。erfinvは誤差関数erfの逆関数です。
μ=\sqrt{2}e_{rfinv}\left(1-2y\right)σ+\ln\left(x\right)
指標の値xと、累積度数yはすでにヒントとなる定数(2.5, 0.61)と(4, 0.82)があるので、以下の部分は定数にできて、
a=\sqrt{2}e_{rfinv}\left(1-2y\right)
b=\ln\left(x\right)
μとσは一次式になりました。
μ=aσ+b
連立一次方程式を解くと、μ=0.709889073996、σ=0.738945909242となりました。
実際にx=2.5とx=4を当てはめると、それぞれy=0.61、y=0.82が得られるので合ってそうです。
最頻値と中央値
μとσが決まれば、最頻値と中央値も計算できます。
最頻値=\exp\left(μ-σ^{2}\right)
中央値=\exp\left(μ\right)
確率密度関数
最後に確率密度関数
f\left(x\right)=\frac{1}{\sqrt{2\pi}sx}\exp\left(-\frac{\left(\ln\left(x\right)-m\right)^{2}}{2s^{2}}\right)
として描画したのがこちらです。
こちらの数式はコピーして編集できますので、他のサイトの指標についても試してみてください。