トピックモデルとその界隈

概要

トピックモデルの概要をまとめ、その界隈のモデルを整理します。

背景

インターネットで「トピックモデル」を検索すると、トピックモデルという言葉が指す範囲が記事によって異なっていたり、時にはトピックモデルの一種であるモデルが =トピックモデルとして記載されていたりします。そのため学習開始時にちょっと混乱しました。

この記事では、まず特定の仕組み「トピックモデル」について概要をまとめ、次にそれ以外の仕組みで「トピックモデル」として紹介されるモデルたちとの関係性について整理したいと思います。

参考書

1. トピックモデル (機械学習プロフェッショナルシリーズ) 講談社
   • 全体像から体系的にまとめられ、分かりやすい本です。
     • 統計学の初心者向けに前提知識を順を追って説明
     • 数式の変形過程の説明が丁寧
   • とはいえ数学が得意でないと、この本の説明だけでは前提知識を理解できないところも多いと思います（というか私がそうでした。別途調べ物が必要でした）。

「トピックモデル」という言葉の定義

明確な解説を見つけられないのですが、「トピックモデル」の定義は文脈によって異なるようです。

• 狭義では、文書の潜在的意味を特定の仕組みで解析するモデル
• 広義では、文書の潜在的意味を解析するモデル全体

この記事では、トピックモデル = 狭義の「トピックモデル」とします。上記の「特定の仕組み」とは上記の参考書でトピックモデルの仕組みとして説明されているものです。

トピックモデルとは

ざっくり

文書データの解析手法として提案された確率的生成モデルの一種です。
文書以外にも応用されています。

確率的生成モデルとは

確率を取り入れて、データの不確実性とモデル推定の不確実性を考慮するモデルです。

• データの不確実性
  ある目的変数yを予測したい時に適切な説明変数（仮にxのみだとします）を設けていたとしても、x=10 という同じ条件で目的変数を10回観測して10回とも同値になるとは限りません。また、そのばらつき具合は x = 5の時と、x = 10 の時では異なるかもしれません。
  確率的生成モデルは、そういった不確実性を平均と分散を用いて確率という形で表現します。

• モデル推定の不確実性
  上記「データの不確実性」で平均と分散が出てきましたが、この平均や分散にも不確実性があります。例えばデータが少なければ平均の不確実性は大きくなります。
  確率的生成モデルは、これらも確率で表現します。

株式会社 Laboro.AIさんのエンジニアコラム確率モデルによる情報処理を参考にさせていただきました。具体的な例を用いて丁寧に説明してくださっています。

HELLO CYBERNETICSさんの【機械学習ステップアップ】確率モデルの考え方で、確率モデルでない回帰問題でよく出てくる最小二乗法による学習と、確率モデルの学習の考え方を分かりやすく比較して説明してくださっています。データの不確実性をこの文中では「ノイズε」として扱っています。

確率的生成モデル と 確率モデル
参考書や記事によって、 　確率的生成モデル = 確率モデル　としたり、　データを生成する確率モデル = 確率的生成モデル（確率的生成モデル ⊂ 確率モデル）　としたり、言葉の定義が異なることがあるようです。どちらの定義でもトピックモデルは確率的生成モデルと言えます。

トピックとは

潜在トピックとも呼ばれます。
複数の単語の共起性によって得られる意味 = 潜在的意味 のカテゴリです。
例えば「金、株式、先物」という単語の塊からは「投資の話かな」と連想されますが、この場合「投資」がトピックとなります。

「共起性によって」というのは、一緒に出現する単語により意味が形成される、ということです。例えば「金、大会、スタジアム」は上記の例にも出てきた「金」という単語を含んでいますが、この例では「スポーツかな？」と連想されます。

トピックの解釈
トピックモデル自体で「投資」「スポーツ」といったトピックのラベリングは出来ません。「このトピックは投資らしい」「スポーツっぽい」というのは、トピック毎の単語分布（後述）を見て人間が解釈します。

トピックモデルで言う「文書」とは

単語の多重集合を「文書」として考えます。
例えば「趣味は口笛です。でも口笛を吹きながら自転車を漕ぐとスピード出ちゃうんですよね。」という文章を「趣味, 口笛, 口笛, 吹く, 自転車, 漕ぐ, スピード, 出る」といった単語の集まりと考えます。

※上記のように文章を単語の集まりとする表現をBOW（Bag-Of-Words）と言います。BOWは上記のような形式とは限りません。実際に処理する際には語彙に語彙IDを付与して語彙ID: 出現回数 の形にすることがよくあると思います。

トピックモデルで言う「共起」とは

「1つの文書内に一緒に出現すること」を意味します。

他のモデルには「共起」=「ウィンドウサイズ内に一緒に出現すること」とするものもあり、「共起」の意味がモデルにより異なることに注意が必要です。

トピックモデルは何を推定するのか

トピックモデルは、なるべく与えられた文書集合っぽい文書集合を生成するように以下の分布のパラメータを推定します。

• トピック分布
• 単語分布

推定過程については、今後別記事にまとめます（目下お勉強中）。

トピック分布

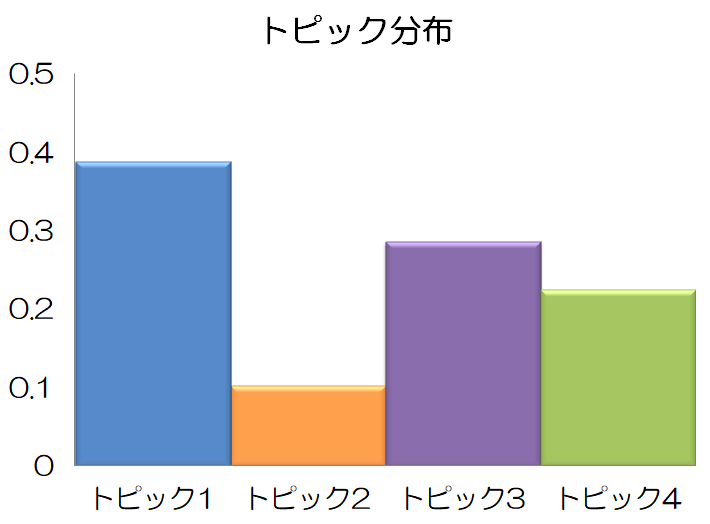
トピックの出やすさを表します。
以下はトピック数が4と仮定した場合の例です。トピック1が最も出やすく、トピック2が最も出にくい分布となっています。

トピック数は基本的に人間が指定しますが、トピック数を推定する方法もあります。（別記事にまとめたいと思います）

単語分布

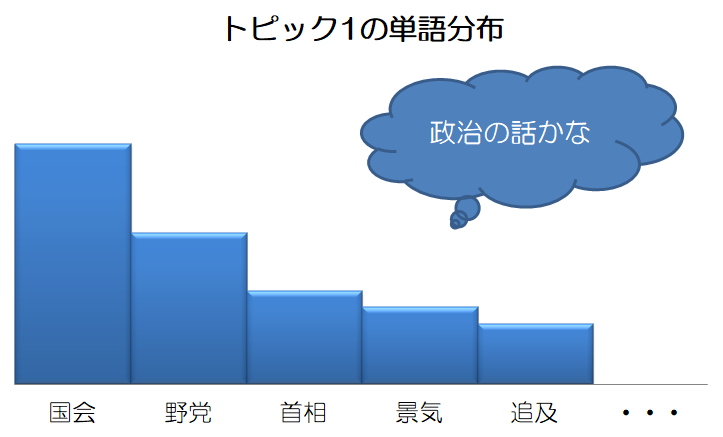
単語の出やすさを表します。
トピックモデルではトピック毎の単語分布を考えます。

例えば、上図のトピック分布に対し、トピック1とトピック2に以下のような単語分布があるとします。（トピック3、4の単語分布も当然ありますがここでは省略します）
異なるトピックで同じ単語が出現することもあり得ます。

トピックとは に記載した通り、トピックモデルが各トピックのラベリングしてくれる（分かりやすいトピック名を付けてくれる）わけではありません。各トピックのラベリングが必要であれば、人間がトピック毎の単語分布を見て解釈します。

トピックモデルの用途

トピックモデルで得られるトピック分布や単語分布を、他の処理と組み合わせて使います。例えば、

• トピック分布を用いて文書をクラスタリング
  • 同様に、顧客の購買履歴で得られたトピック分布（≒顧客の傾向）を用いて顧客をクラスタリング
• トピック分布を用いて文書間の類似度を得る
• トピック分布と単語分布を用いて文書検索
  • 検索対象の単語を直接含まない文書でも、分布を介することにより関連性の高さでヒット

などがあります。

トピックモデル界隈の主なモデルたち

広義のトピックモデルたちと、ここまで記載した（狭義の）トピックモデルとの関係を整理したいと思います。

記事先頭の図を再掲します。
ここでは、（狭義の）トピックモデルを理解するために前提として知っておきたいモデルや、トピックモデルとしてよくヒットするモデルを記載しています。

ユニグラムモデル → 混合ユニグラムモデル → トピックモデル

すべて確率的生成モデルです。この順に仕組みが複雑化していきます。
この記事では扱いませんが、推定過程について理解しようとするときにこの順で追っていくと理解しやすいです。（上述の参考書でこの順で説明しています）

ユニグラムモデル

ユニグラムモデルには、文書がトピックを持つという概念がありません。
グラフィカルモデル表現¹で表すと下図のようになります。
単語分布$Φ$が1つだけ存在し、すべての文書の単語は$Φ$から生成されると仮定するシンプルなモデルです。

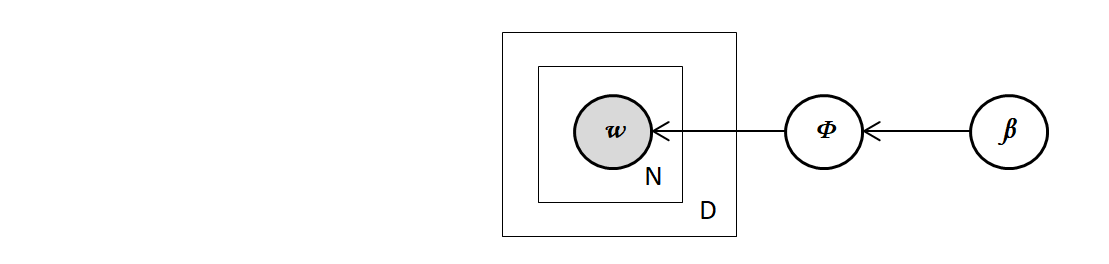
• $β$：単語分布のパラメータ
• $Φ$：単語分布
• D ：文書数
• N ：文書内の単語数
• $w$：単語（観測データ）

混合ユニグラムモデル

ユニグラムモデルにトピックの概念が入り、1つの文書が1つのトピックを持つと仮定するモデルです。

全体で1つのトピック分布$Θ$を持ち、トピック分布$Θ$から文書ごとにトピック$z$を生成します。
一方、単語分布をトピック毎に生成します。トピック数をK個とすると単語分布はK個になります。
そして文書内の単語をトピック$z$（トピック1～Kのどれか）の単語分布$Φ$から生成していきます。

つまり、混合ユニグラムモデルは

• トピック数K回
  • トピックKの単語分布を生成
• 文書数D回
  • その文書のトピック$z$（トピック1～Kのどれか）生成
  • その文書の単語数N回
    • $z$の単語分布$Φ$から単語$w$生成

という流れで文書集合を生成していきます。

• $α$：トピック分布のパラメータ
• $Θ$：トピック分布
• $z$：トピック
• $β$：単語分布のパラメータ
• $Φ$：単語分布
• $k$：トピック数
• D ：文書数
• N ：文書内の単語数
• $w$：単語（観測データ）

トピックモデル

1つの文書が複数のトピックを持つと仮定するモデルです。

例えば「CMと株価」についての文書には「マーケティング」と「投資」の2つのトピックが含まれています。混合ユニグラムモデルでは1文書1トピックを仮定しているため、これを表現するには「マーケティング＋投資」という1トピックと考えることになります。すると「マーケティング＋投資」の単語分布も必要になります。同様に「経済＋投資」「技術＋投資」など推定すべき単語分布が膨大になり適切に推定できないという問題が起こります。

トピックモデルはこのような問題を解決します。
上述の「1つの文書が複数のトピックを持つ」というのは、具体的に言うと「文書ごとにトピック分布を持つ」ということです。「CMと株価」についての文書は「マーケティング」と「投資」の2つのトピックが出やすいトピック分布を持つ文書となるでしょう。

トピックモデルは

• トピック数K回
  • トピックKの単語分布を生成
• 文書数D回
  • その文書のトピック分布$Θ$を生成
  • その文書の単語数N回
    • $Θ$からトピック$z$（トピック1～Kのどれか）生成
    • $z$の単語分布$Φ$から単語$w$生成

という流れで文書集合を生成していきます。

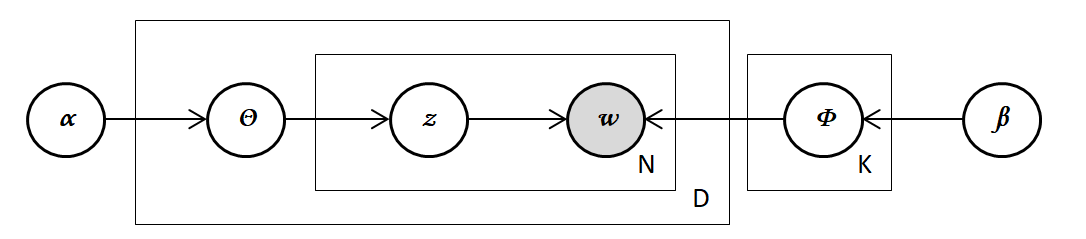
• $α$：トピック分布のパラメータ
• $Θ$：トピック分布
• $z$：トピック
• $β$：単語分布のパラメータ
• $Φ$：単語分布
• $k$：トピック数
• D ：文書数
• N ：文書内の単語数
• $w$：単語（観測データ）

文書集合を生成って・・・観測データでしょ??
「文書集合を生成します」と書きましたが、私が学習開始当初にトピックモデルの説明で良く分からなかった点がここでした。観測データ（与えられた文書）を生成するってどういうこと？と。その後トピックモデルは何を推定するのかを知ってようやく意味が分かりました。

LSA/LSI と PSLA/PLSI

LSA/LSI は特異値分解を利用して次元削減し潜在的意味を得ようとするモデルです。LSA/LSI の問題点を解消すべく確率モデルとして再定式化してできたモデルが PSLA/PSLI です。

PLSAとPLSIの違い
[Wikipedia] (https://en.wikipedia.org/wiki/Probabilistic_latent_semantic_analysis)によると、PLSA = PLSIですが、特に情報検索の用途の場合にPLSIと呼ぶようです。PLSAはProbabilistic Latent Semantic Analysis：確率的潜在意味解析、PLSIはProbabilistic Latent Semantic Indexing：確率的潜在的意味索引の略です。LSAとLSIの関係も同様です。

PSLA/PLSI と LSA

どちらもトピックモデルです。
PLSA/PLSIは最尤推定する手法、LDAはトピック分布にディリクレ事前分布を仮定しベイズ推定する手法です。

トピックモデルは何を推定するのかに記載した通り、それぞれの手法について今後別記事にまとめていきたいと思います。

（doc2vec）

ニューラルネットワーク型のdoc2vec で得られる文書の分散表現は文書の潜在意味を表していると思うのですが、トピックモデルとして紹介されているケースを見たことがありません（私が見つけられなかっただけかもしれませんが）。潜在意味を解析するということとは観点が違うのかな。。。
※doc2vec は厳密には実装を指す言葉のようですが、ここでは一般的に用いられているようにモデル名として記載しています。

1. 確率変数間の因果関係を図示したもの ↩