概要
計算グラフの逆伝播でtanhの微分を求めるお題にトライ。
前提:計算グラフって?
- 計算グラフとは、計算の過程を図示したようなもの。
-
ゼロから作るDeep Learning でとても分かりやすく説明している。
- オライリーで電子書籍も入手可能
- TensorFlowの「データフローグラフ」も上記の本を読んでおくととても理解しやすい。
tanh の式
\begin{align}
\tanh x&=\frac{\sinh x}{\cosh x} \\
&=\frac{\frac{e^x-e^{-x}}{2}}{\frac{e^x+e^{-x}}{2}} \\
&=\frac{e^x-e^{-x}}{e^x+e^{-x}}
\end{align}
自分の回答
以下で求めたtanhの微分と、調べたtanhの微分は一致したので、解けているみたい。
自分が分かりやすいように式を変形して計算グラフを作ったけど、普通は割り算のまま描くのかな?
その後教えていただいた回答も、分数は掛け算の形に変形していた。
分数のままでも微分は出来るのでそれでも正解のはずだが、掛け算に変形した方が逆伝播にシンプルな微分の法則を適用できる。
1. 前準備:tanhの式を変形
数学苦手な自分が逆伝播を描きやすくするため、以下のように変形した。
- 分母を-1乗して、掛け算の形に変形
- 引き算$A-B$ は $A+(-B)$ として、足し算の形に変形
\frac{e^x-e^{-x}}{e^x+e^{-x}}=\bigl({e^x+(-e^{-x})}\bigr)*(e^x+e^{-x})^{-1}
2. 計算グラフの順伝播を描く
1で変形した式を元に順伝播を描く。
- 以下の記載ルールで描いた
- グラフの〇は、演算内容を示す。
- グラフの矢印は、計算の途中結果を示す。
3. 計算グラフの逆伝播を描く
- 前提知識
- 連鎖律
- 微分関連の公式が少し
- ネイピア数eについて、$(e^x)'=e^x$
右端から微分していった。
ハートウォーミングな手描きを掲載・・・
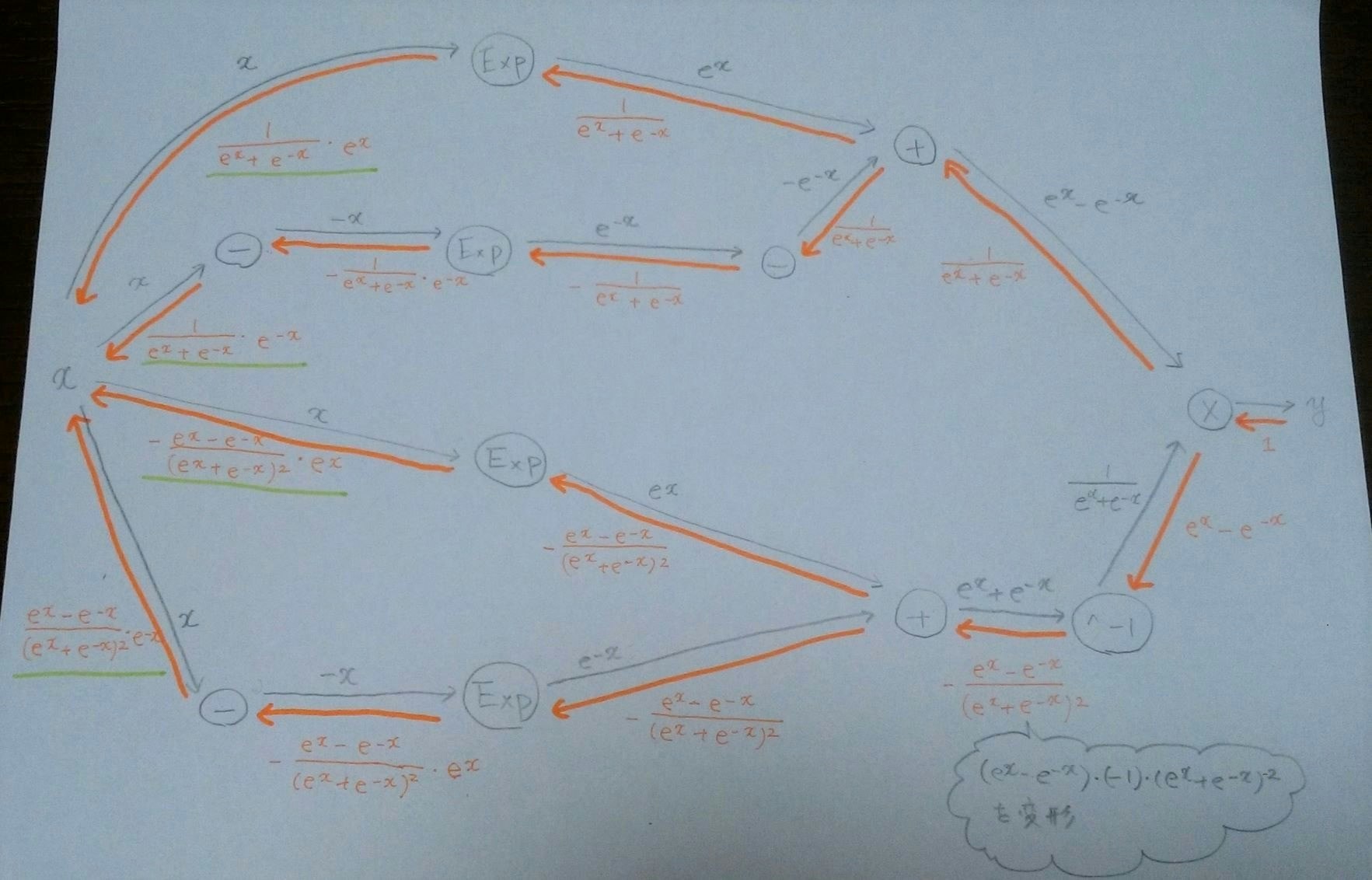
4. 計算グラフから求めたtanhの微分
上のtanhの計算グラフの黄緑で示した式(逆伝播の最終式)を合算。
\begin{align}
&\frac{1}{e^x+e^{-x}}*e^x+\frac{1}{e^x+e^{-x}}*e^{-x}-\frac{e^x-e^{-x}}{(e^x+e^{-x})^2}*e^x+\frac{e^x-e^{-x}}{(e^x+e^{-x})^2}*e^{-x} \\
&=\frac{1}{e^x+e^{-x}}*(e^x+e^{-x})-\frac{e^x-e^{-x}}{(e^x+e^{-x})^2}*(e^x-e^{-x}) \\
&=\frac{e^x+e^{-x}}{e^x+e^{-x}}-\frac{(e^x-e^{-x})^2}{(e^x+e^{-x})^2} \\
&=1-\biggl(\frac{e^x-e^{-x}}{e^x+e^{-x}}\biggr)^2 \\
&=1-\tanh^{2} x
\end{align}
5. 教えていただいた解
\frac{4}{\bigl(e^x+e^{-x}\bigr)^2}
自分の回答とは形は異なるが実質同じ、とのこと。。。
一緒にいただいた計算グラフは形は違くても同じことをやっているのは分かった。
しかし、この式は私には違う解に見えてしまう。。。
と納得がいかず、続き。
実際、$\tanh x$ の微分としては上記両方正しい。
ならば $1-\tanh^{2} x=\frac{4}{(e^x+e^{-x})^2}$ に変形できるはずなのでトライ。
関係式 $\cosh^2 x-\sinh^2 x=1$ を利用して解決、すっきりした。
\begin{align}
1-\tanh^{2} x=&1-\frac{\sinh^2 x}{\cosh^2 h} \\
&=1-\frac{\cosh^2 {x-1}}{\cosh^2 x} \\
&=\frac{\cosh^2 x-\cosh^2 x+1}{\cosh^2 x} \\
&=\frac{1}{\cosh^2 x} \\
&=\frac{1}{\biggl(\frac{e^x+e^{-x}}{2}\biggr)^2} \\
&=\frac{4}{\bigl(e^x+e^{-x}\bigr)^2}
\end{align}
私の解$1-\biggl(\frac{e^x-e^{-x}}{e^x+e^{-x}}\biggr)^2$よりも、教えていただいた形の解の方が処理速度が上がる、など性能上の違いはあるんだろうか。