アルゴリズムイントロダクション 練習問題1.2

本記事の概要

概要はこちら

第一回の記事を参照ください。
さっそく回答していきます。
（第一回の記事でも申し上げましたが、私の回答は正解ではないですし、間違ってる可能性大！です。）

練習問題1.2

紙で計算したりする問題増えてきましたね！
プログラムも書いて回答していきます。

1.2-1

アプリケーション層でアルゴリズムが必要になる応用の例を挙げ、必要とされるアルゴリズムの機能を議論せよ。

書籍では地図アプリの最短経路探索を紹介されていましたね。

回答
例えばオセロのゲームアプリを例に挙げてみます。
専門家ではないので、予想になりますが、
盤面の評価関数に基づき、n手先までの盤面を評価し、最も有利な手を選択するという手法を用いると思います。
n手先まで予想する場合、およそnの累乗のような形で実現し得る盤面が存在します。
（序盤や終盤はおける場所が限られているので底は小さいが、中盤は底が大きな値を取る。）
もちろんなるべく先の手順まで読んだほうが強くなりそうなので、nは大きな値を取りたいですが、
計算時間が増え過ぎるのはユーザー体験として良くないでしょう。
探索のアルゴリズムを効率的にすることにより、限られたリソースで最も良い手を選択することができると思います。（小並感）

1.2-1

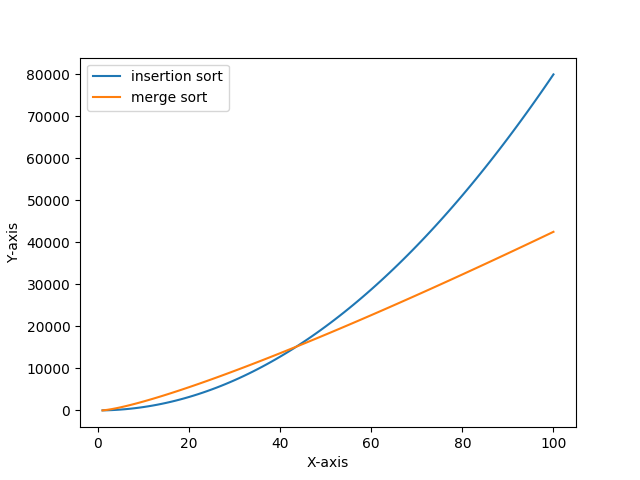
同じ計算機上で挿入ソートとマージソートの実現を比較する。サイズ$n$の入力に対し、挿入ソートの実行には$8n^2$ステップかかり、一方、マージソートの実行には$64n\log_2 n$ステップかかるとする。挿入ソートがマージソートに優る$n$の値を調べよ。

回答
これ普通に高校数学で方程式解けるんでしたっけ？(汗)
まあ、サイズを整数として扱えば計算していけばわかります。
調べよとのことなのでpythonに調べてもらいました。

1.2-2.py

# -*- coding: utf-8 -*-
import math
import numpy as np
from matplotlib import pyplot


def main():
  x = np.linspace(1, 100, 100)
  y1 = 8 * (x ** 2)
  y2 = 64 * x * np.log2(x)
  pyplot.plot(x, y1, label="insertion sort")
  pyplot.plot(x, y2, label="merge sort")
  pyplot.legend()
  pyplot.xlabel("X-axis")
  pyplot.ylabel("Y-axis")
  filename = "1.2-2.png"
  pyplot.savefig(filename)


if __name__ == '__main__':
  main()

およそ43くらいですかね。
$n$はサイズなので整数として扱います。43前後の整数をいくつか実際に計算して調べましょう。
対話モードで検証します。compare関数で計算時間の小さい方のアルゴリズムを出力します。

>>> def insertion(x):
...     return 8 * (x ** 2)
...
>>> import numpy as np
>>> def merge(x):
...     return 64 * x * np.log2(x)
...
>>> def compare(x):
...     return 'merge' if merge(x) < insertion(x) else 'insertion'
...
>>> compare(42)
'insertion'
>>> compare(43)
'insertion'
>>> compare(44)
'merge'
>>> compare(45)
'merge'

上記の通り、サイズ43までは挿入ソートが優り、サイズ44以上はマージソートに軍配があがります。

1.2-3

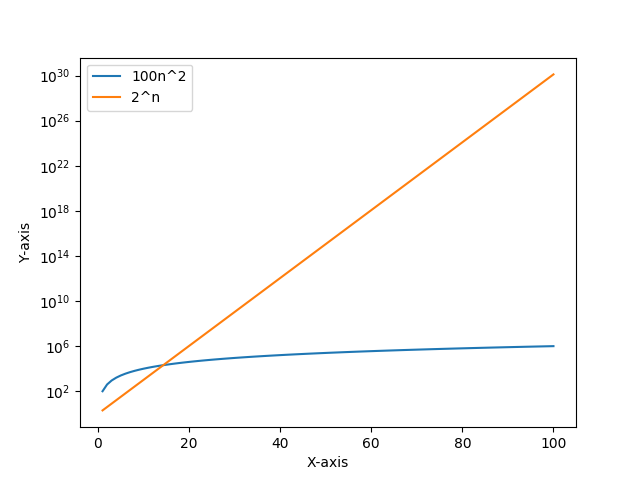
同じ計算機上で、実行時間が$100n^2$のアルゴリズムが、実行時間が$2^n$のアルゴリズムより高速に実行できる最小の$n$の値を調べよ。

回答

1.2-3.py

# -*- coding: utf-8 -*-
import math
import numpy as np
from matplotlib import pyplot


def main():
  x = np.linspace(1, 100, 100)
  y1 = 100 * (x ** 2)
  y2 = np.power(2, x)
  pyplot.plot(x, y1, label="100n^2")
  pyplot.plot(x, y2, label="2^n")
  pyplot.legend()
  pyplot.xlabel("X-axis")
  pyplot.ylabel("Y-axis")
  pyplot.yscale("log") 
  filename = "1.2-3.png"
  pyplot.savefig(filename)


if __name__ == '__main__':
  main()

y軸は対数目盛です。

だいたい13～14くらいかな。
これも調べてみましょう。

1.2-3.sch

(define (min_n n)
    (if (< (y1 n) (y2 n))
        (- n 1)
        (min_n (+ n 1))))

(define (y1 n)
    (* 100 (expt n 2)))

(define (y2 n)
    (expt 2 n))

(print (min_n 1))

>14

唐突のscheme。
$2^n$の方が大きくなったときの一個前のnを返却するmin_n関数により14と求められました。
めでたしめでたし。

次回

今回は超かんたんなプログラムだけど色々計算できて楽しかったです。
もうちょっと紙で計算してみればよかったのかな。
MITの教科書ということですが、MITの学生はどうしてるのかな。。

次回は章末問題やっていきますか！！