Nuco Advent Calendar 13日目の記事です。
Bitcoin
最早毎日のようにニュースやSNSで仮想通貨の話題を目にするようになりました。
私も個人的に投資目的でいくつか仮想通貨を購入していますし、
マイニングリグを組み立ててマイニングもしています。
価格が不安定なので、通貨としてというよりも投資目的で仮想通貨を購入している人が今は多いと思います。
多少デイトレードも行ってますが、基本的には長期的に保持して資産が増えていくのを楽しんでます。
そうなれば気になるのは将来的にBitcoinがいくらくらいになるのかが知りたいですね。
よし、やってみようではないか。
ロジスティック方程式
僕は経済学などには特に詳しくないのですが、
通貨の価値が高まれば高まるほど、通貨を欲しがる人は増えるでしょう。
通貨を欲しがる人が増えれば増えるほど通貨の価値は高まります。
と考えられます。
そうなれば線形な関数よりも非線形に増えていくほうが自然な気がします。
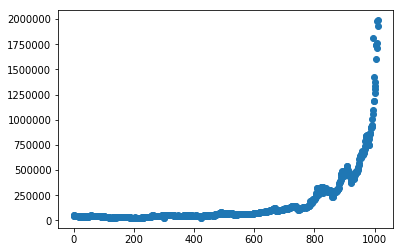
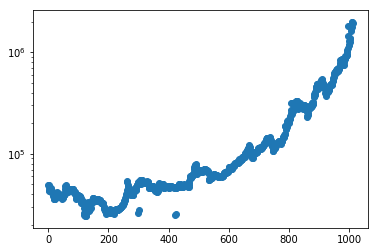
実際に過去のBitcoinは線形関数よりも指数関数の方がよく近似できます。
Excelなどで対数目盛を使うと直線に近づくのがわかると思います。
指数関数で近似しても良いのですが、
感覚的に将来の価格はどこかのタイミングで頭打ちになると考えた方が自然でしょう。
それがどのくらいの価格になりそうなのか知りたいですね。
そこで出て来るのがロジスティック方程式です。
生物の個体数増加のモデルとして知られます。
生物の個体数は個体数が増えれば増えるほど、増加率も大きくなりますが、
環境収容力(土地や食料など)によって制限がかかり、やがて増加が頭打ちになります。
このロジスティック方程式にフィッティングさせれば、将来どのくらいの価格になるか、予想できるかもしれません。
フェルフルストモデル
1838年にベルギーの数学者Pierre Verhulst(フェルフルスト)によって考案されたモデルです。
具体的には下記の微分方程式になります。
$\frac{dN}{dt}=r_{0} N(1 - \frac{N}{K})$
上記の解は、
$N_{t} = \frac{N_{0}K}{N_{0} + (K - N_{0}) e^{ - r_{0}t}}$
|記号|意味|
|:---|:---|:---|
|$r_{0}$|平衡水準に近づく速さ|
|$K$|環境収容力|
|$N_{0}$|$t=0$のときの値|
|$N_{t}$|時間$t$のときの値|
こちらのモデルのパラメータを最小二乗法で求めてみます。
最小二乗法
ライブラリはScipyを用います。
Scipyにはleastsqという最小二乗法フィッティングソルバがありますので、こちらを使います。
下記が実際のソースコードです。
実行環境はUbuntu14.04, python3, jupyter notebookです。
df = pd.read_csv('./btc_jpy.csv', thousands=',')
df = df[0:-2]
high = df['高値'].apply(lambda x: x.replace(',','')).astype(np.int)
low = df['安値'].apply(lambda x: x.replace(',','')).astype(np.int)
median = ((high + low) / 2).astype(np.int)
df = DataFrame({'date': df['日付け'], 'median': median})
df = df[::-1]
df.index = range(len(df))
データをいい感じに整形します。
1日ごとの高値と安値の平均を使います。
def logistic_model(param, x, y):
N0 = 49107
r0 = param[1]
K = param[0]
y0 = 0
Nx = y - N0 * (K/(N0+(K-N0)*np.exp(-r0*x)))
return Nx
r, info = leastsq(logistic_model, [100000, 0.1], args=(df.index, df['median']))
r
>[ 4.60186206e+12 2.53551510e-03]
こちらでparameterを算出します。
このパラメータを用いて、
def predict(x):
N0 = 49107
r0 = 2.85628441e-03
K =6.53673303e+12
y0 = 0
return N0 * (K/(N0+(K-N0)*np.exp(-r0*x)))
fig = plt.figure()
ax1 = fig.add_subplot(1,1,1)
ax1.scatter(df.index, df['median'], label='actual', color='blue', marker='o')
ax1.scatter(df.index, predict(df.index), label='predict', color='red',marker='x')
fig.show()
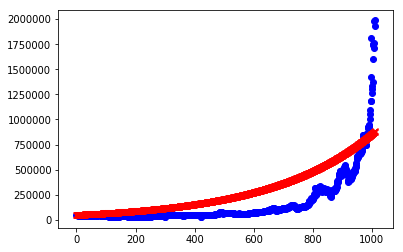
実際にプロットして比べてみます。
うーん。。あまり上手くいきませんね。。
ビットコインの価格の上がりが強すぎるのと、変曲点を越えて頭打ちになり始めないとフィッティングは難しいようです。。
まとめ
目的は果たせませんでしたが、Scipyなどのパッケージを使った非線形関数へのフィッティングの実装ができたので、
何かおもしろい題材があればまたやってみたいと思います。