はじめに
この記事は、以下PDFを多分に参考にさせていただきました。
この場を借りて、厚く御礼申し上げます。
CCD-IKのアルゴリズムなどについても詳しく述べられていますので、より詳しく知りたい方は、ぜひこちらもご覧ください。
CCD-IK and Particle-IK - TMPSwiki
https://mukai-lab.org/content/CcdParticleInverseKinematics.pdf
IK(Inverse Kinematics)とは
人間の腕(肩-ひじ-手首)のように、各関節(ジョイント)が連動しており、末端のジョイントを目標地点に置くために、各ジョイントの角度を自動計算する方式。
何か物を取る時に、ひじの角度を意識せず、手首の位置を物の近くに持っていくような動作の事です。
IKが計算出来ると何が嬉しい?
物を取るときに、肩やひじの角度をいちいち意識して(計算して)手首の位置を物の近くに近づけようとするより、手首の位置だけを意識して、肩やひじの角度は可動範囲内であれば特に気にしない、という方が、処理の省略ができます。
コードサンプル(Colab)
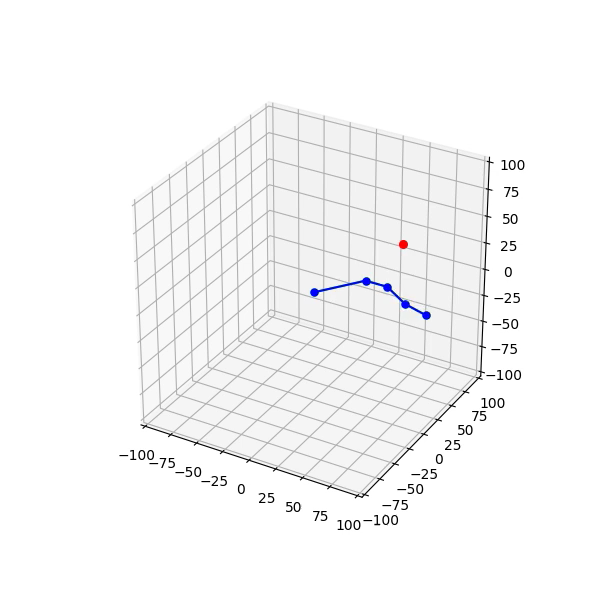
上記参考文献のコードをpythonに書き直し、上記gifのようにアニメーションでIKの動きを視認できるサンプルをColab上に作成しました。
Playgroundで開いて、実行してみてください。
アニメーションの生成に若干時間がかかります。
目標地点などを適当に変更すると、動きが変わります。
(-100~100の範囲外ですと、図からはみ出る可能性があります)
IKの処理概要
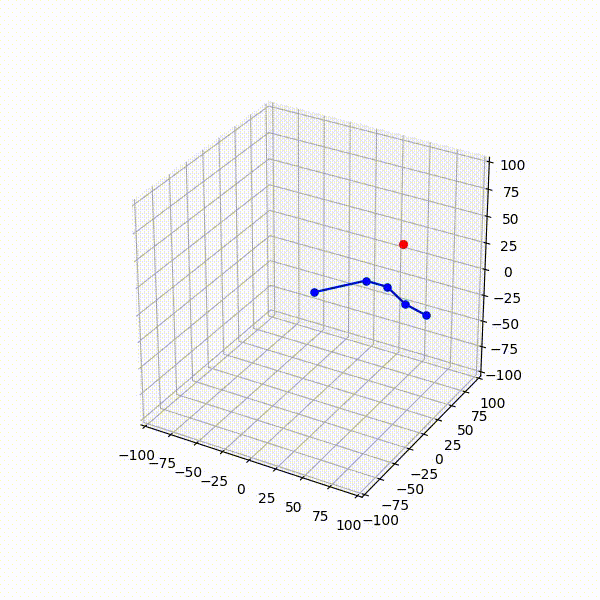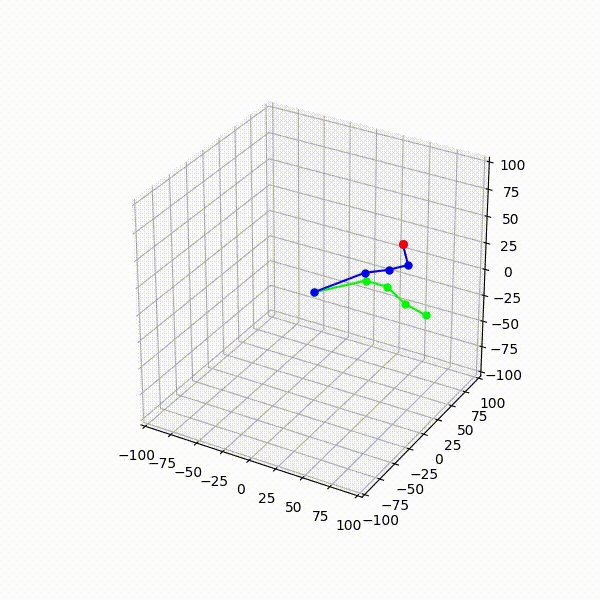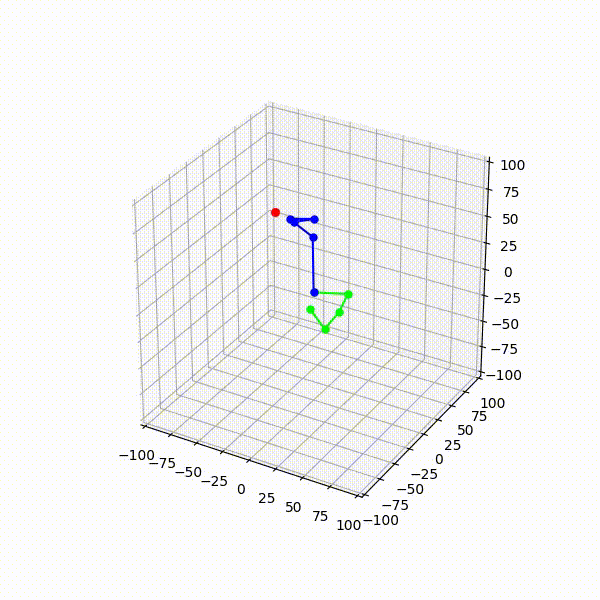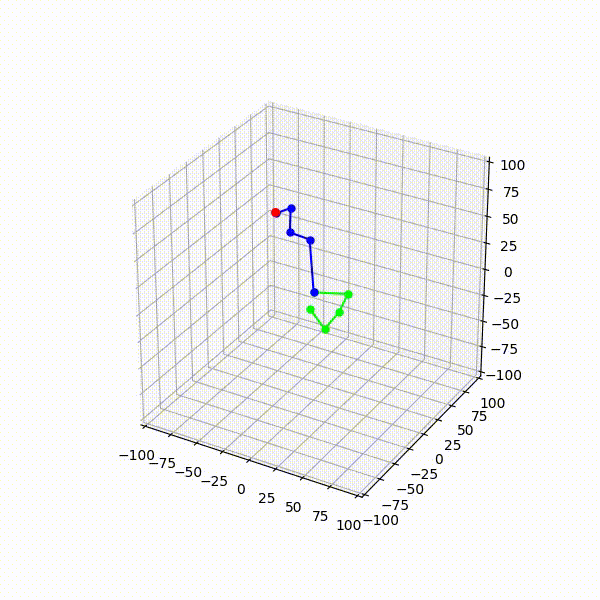
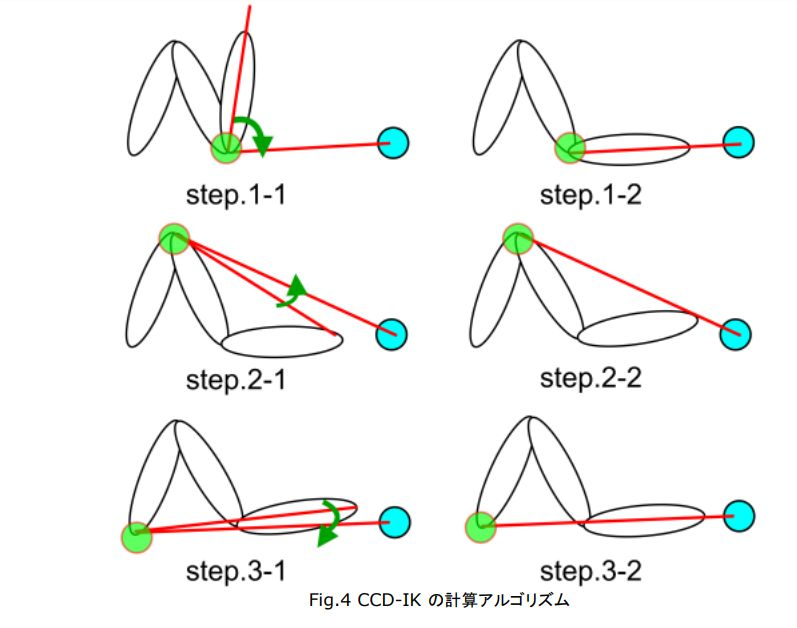
CCD 法では,この計算ステップをエフェクタに近い関節からルート関節に向かう順に繰り返し適用することで,スケルトン全体としての最適解を求めます.この繰り返し手順と,それに伴うスケルトン姿勢の変化の例を Fig.4 に示します.ここで,青丸がスケルトンのエフェクタの到達目標位置,緑丸が各計算ステップでの注目関節を示します.
- step.1-1:エフェクタに最も近い関節から,エフェクタに向かうベクトルと目標位置に向かうベクトルをそれぞれ計算
- step.1-2:2 つのベクトルを利用して,エフェクタに最も近い関節の回転量を修正
- step.2-1:中間の関節から,エフェクタに向かうベクトルと目標位置に向かうベクトルをそれぞれ計算
- step.2-2:2 つのベクトルを利用して,中間の関節の回転量を修正
- step.3-1:ルート関節から,エフェクタに向かうベクトルと目標位置に向かうベクトルをそれぞれ計算
- step.3-2:2 つのベクトルを利用して,ルート関節の回転量を修正
- step.4:step.1-1 から再度繰り返し
引用元: CCD-IK and Particle-IK - TMPSwiki
簡単に言うと、関節の角度を目標地点の方向に向くよう変更する、それを末端から親に向けて順番に行い、それを一定回数反復することで、目標地点に近づける、というアルゴリズムです。
コード解説
※引用元PDFのJavaコードをpython用に変換したものです。
※本コードはPyQt5ライブラリを使用しております。
1. 初期データを用意する
初期データとして、以下を準備します。
- ジョイントデータ(青い点)
- IKとして動かす関節位置データ(グローバル座標)
- クラス:
Joint
# 関節データを親から登録していく
joints = []
joints.append(Joint("J1", QVector3D(0, 0, 0)))
joints.append(Joint("J2", QVector3D(40, 15, 15)))
joints.append(Joint("J3", QVector3D(60, 15, 15)))
joints.append(Joint("J4", QVector3D(80, 15, 15)))
joints.append(Joint("J5", QVector3D(100, 15, 15)))
- モーションデータ(青い線(点の向き))
- ジョイントのフレームごとの回転量データ(クォータニオン)
- クラス:
JointMotion
# モーションデータを全関節分の初期データを用意する(関節名をキーとする)
motions = {}
motions["J1"] = JointMotion(0, "J1", QQuaternion.fromEulerAngles(0, 0, 0))
motions["J2"] = JointMotion(0, "J2", QQuaternion.fromEulerAngles(10, 0, 0))
motions["J3"] = JointMotion(0, "J3", QQuaternion.fromEulerAngles(0, 40, 0))
motions["J4"] = JointMotion(0, "J4", QQuaternion.fromEulerAngles(0, 0, 20))
motions["J5"] = JointMotion(0, "J5", QQuaternion.fromEulerAngles(0, -20, 0))
- 目標グローバル位置(赤い点)
- IKの末端ジョイントが最終的に置かれるべき位置(グローバル座標)
# 各フレームごとの目標グローバル位置
target_poss = []
target_poss.append(QVector3D(50, 60, 30))
target_poss.append(QVector3D(20, -40, 10))
target_poss.append(QVector3D(-60, 40, 40))
2. IK計算処理を行う
IK計算は常に末端から親に向かって処理していきます。
そして、親まで処理が終わったら、それを規定回数分反復します。
# 関節は末端から処理していくため、事前に反転させたリストを生成しておく
reversed_joints = list(reversed(joints))
# 最大反復回数分ループ
for idx in range(maxc):
# 末端から処理していくため、リバース
for eidx, effector in enumerate(reversed_joints):
# エフェクタは末端
effector_idx = 0
エフェクタ=末端ジョイントです。
末端から処理していくため、常に0番目の要素がエフェクタとなります。
# ジョイントは、現在の処理対象の親
joint_idx = eidx + 1
# ジョイントデータ
joint = reversed_joints[joint_idx]
# ジョイントモーションデータ
joint_motion = joint_motions[joint.name]
実際に回転角度を調整するジョイントは、ループで処理している要素のひとつ親となります。
ジョイントデータ(関節の配置)とモーションデータ(関節の現在回転量)を取り出しておきます。
# ルートからのグローバル位置と行列生成
global_poss, comp_matrixs = create_globalpos_matrix(joints, joint_motions)
# グローバル位置をリバース
reversed_global_poss = list(reversed(global_poss))
# ルートからの合成行列をリバース
reversed_comp_matrixs = list(reversed(comp_matrixs))
# エフェクタのグローバル位置
global_effector_pos = reversed_global_poss[effector_idx]
# 注目ノードのグローバル位置
global_joint_pos = reversed_global_poss[joint_idx]
まず、ジョイントデータとモーションデータから、現在のジョイント(以降、注目ノード)のグローバル位置を求めます。
詳細はメソッドの中を参考にしてください。
グローバル位置は一番上の親から求めるため、求めた後、リバースしたリストを保持しておきます。回転行列も同様にリバースしておきます。
(そうするとインデックス処理が楽です)
# ワールド座標系から注目ノードの局所座標系への変換
inv_coord = reversed_comp_matrixs[joint_idx].inverted()[0]
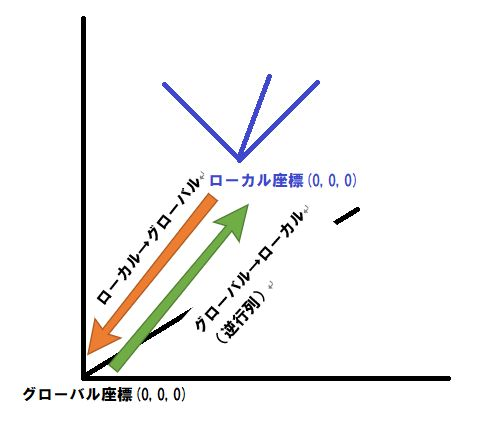
一番上の親から累積した行列データは、そのジョイントのグローバル座標系内の位置を表しています。
その逆行列は、そのジョイントのローカル座標系内の位置を表します。
もうちょっと言うと、ローカル座標系の原点をグローバル座標系の原点に移動したのが、comp_matrixs 行列で、グローバル座標系の原点から見たローカル座標系の原点の位置が、グローバル座標の位置として求めることのできる行列となっています。
その逆は、ローカル座標系の原点から見たグローバル座標の位置を求める事ができる行列なのです。
# 注目ノードを起点とした、エフェクタのローカル位置
local_effector_pos = inv_coord * global_effector_pos
local_target_pos = inv_coord * target_pos
という事で、現在の注目ノードの原点から見た、エフェクタの位置と目標地点の位置が逆行列をかけることで求められます。
# (1) 基準関節→エフェクタ位置への方向ベクトル
basis2_effector = local_effector_pos.normalized()
# (2) 基準関節→目標位置への方向ベクトル
basis2_target = local_target_pos.normalized()
正規化して、単位方向ベクトル(直線が延びている方向を指し示す大きさ1のベクトル)をそれぞれ求めます。
「どのくらい離れているか」は問題ではなく、「どの方向にいるか」だけが問題であるためです。
# ベクトル (1) を (2) に一致させるための最短回転量(Axis-Angle)
# 回転角
rotation_dot_product = QVector3D.dotProduct(basis2_effector, basis2_target)
# 念のため0~1の間に収める
rotation_dot_product = 1 if rotation_dot_product > 1 else rotation_dot_product
rotation_dot_product = 0 if rotation_dot_product < 0 else rotation_dot_product
# 回転角度
rotation_angle = acos(rotation_dot_product)
エフェクタと目標地点の内積から、「注目ノードをどのくらい回転させたらエフェクタの方向と目標地点の方向が合うか」を求めます。
(内積は0~1のはずですが、何かの拍子でその範囲から外れた値が出たことがあったため、念のため範囲内に収めています)
if abs(rotation_angle) > 0.0001:
# 一定角度以上の場合
# 回転軸
rotation_axis = QVector3D.crossProduct(basis2_effector, basis2_target)
rotation_axis.normalize()
rotation_degree = degrees(rotation_angle)
# 関節回転量の補正
correct_qq = QQuaternion.fromAxisAndAngle(rotation_axis, rotation_degree)
# ジョイントモーションに補正をかける
joint_motion.rotation = correct_qq * joint_motion.rotation
回転角度が一定以上の場合、エフェクタと目標地点の外積から回転軸を求め、回転軸と回転量から補正クォータニオンを生成します。
その補正クォータニオンを、注目ノードの回転量にかけることで補正します。
# 回転の差がほとんどない場合、終了
if (local_effector_pos - local_target_pos).lengthSquared() < 0.0001:
return
エフェクタと目標地点のグローバル座標位置の差がほとんどない場合、反復を途中で止めます。
これを繰り返すことで、IK計算ができます。
以上。
不備・不明点等ございましたら、ご指摘ください。