そもそも回帰とは？

回帰（かいき、英: regression）とは、統計学において、Y が連続値の時にデータに Y = f(X) というモデルを当てはめる事。別の言い方では、連続尺度の従属変数（目的変数）Yと独立変数（説明変数）Xの間にモデルを当てはめること。X が1次元ならば単回帰、X が2次元以上ならば重回帰と言う。Wikipedia

つまり、回帰の目的は連続値の予測に着地する。
例えば・・・・
ある人の年収（目的変数)を、学歴と年齢と住所（説明変数）から予測する事。
トウモロコシ農家の収穫量(目的変数)を、前年の収穫量、天候、従業員数（説明変数）から予測する事。

では、線形モデルによる回帰とは

線形モデルによる回帰とは文字通り、線形関数を用いて目的変数を予測するものです。

回帰問題での線形モデルによる一般的な予測式は、

y = w[0] \times x[0] + w[1] \times x[1] + \dots + w[p] \times x[p] + b

と表せます。

ここでx[0]・・・x[p]は１データポイントの特徴量を示し、w, bは学習されたモデルのパラメータであり、yはモデルからの予測である。

つまり訓練データから最適化されたw, bを求め（学習し）,新しいx[0]・・・x[p]を入れられたときに、
出来るだけ正確なyを出力することに帰着する。

ここで線形モデルを用いた回帰には様々なアルゴリズムが存在する。
それらのモデルの相違点は、w, bを求める(学習する）方法とモデルの複雑さを生業する方法に存在する。

今日は最も単純で古典的な線形回帰手法である通常最小二乗法（OLS）について触れたいと思う。

通常最小二乗法（OLS）

それでは簡単にするために、1つの説明変数で考えましょう。
つまり数式は

y = wx + b

この線形回帰では訓練データにおいて、yと予測値の平均二乗誤差が最小になるようにw, bを求める。
文章じゃわかりづらいので画像で考えると下記です。

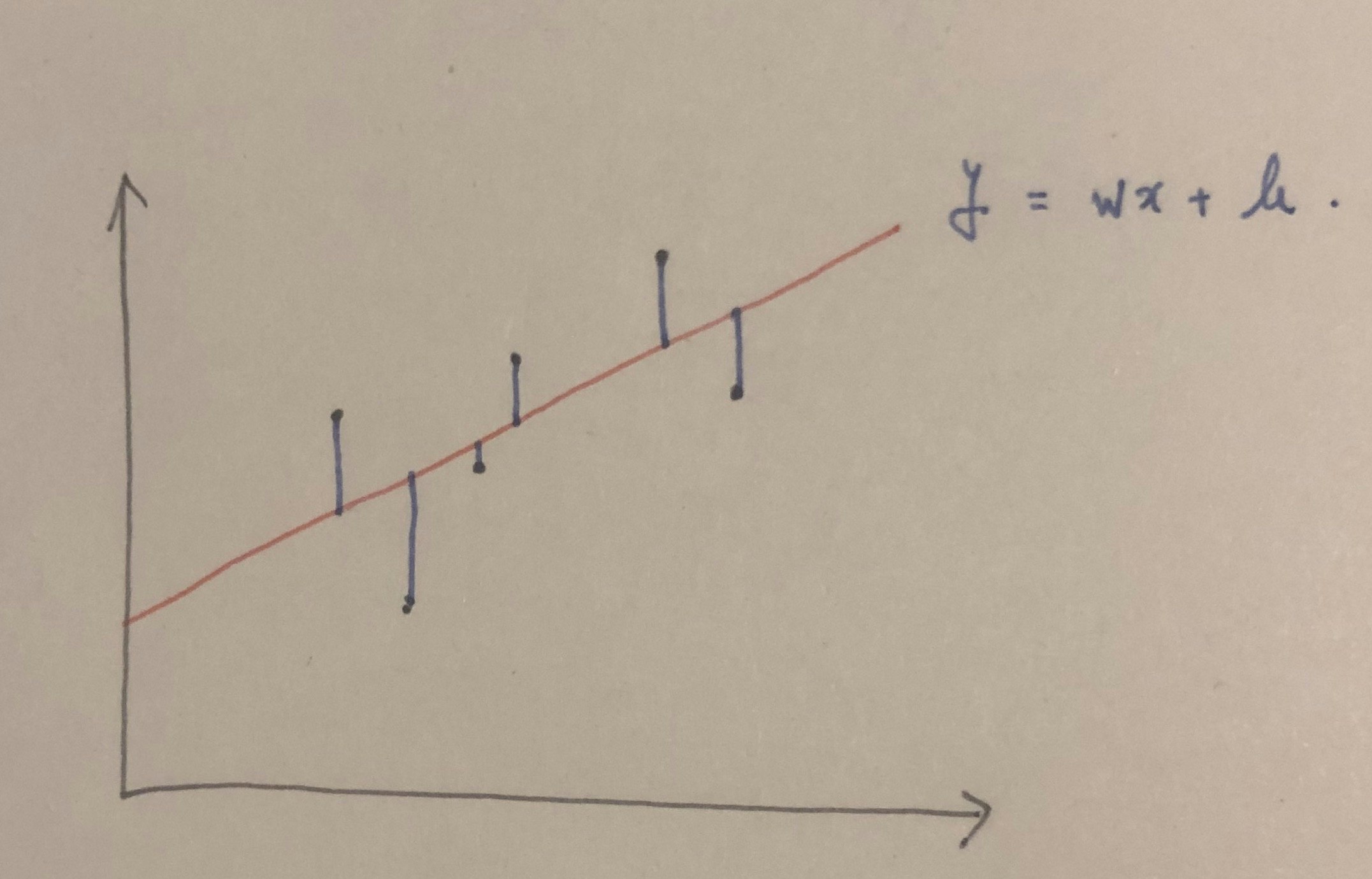
つまり青い線（誤差）の長さの二乗和が出来るだけ小さくなるようにwとbを求めて、その結果が赤い直線となります。

数式で書くならば

平均二乗誤差=\frac{1}{n}\sum_{i=1}^{n} (y_i - y'_i)^2,  (y_i:i番目の訓練データでの値, y'_i: i番目の予測値)

この平均二乗誤差が小さくなるように、w, bを選んでいきます。
これがOLSです。簡単で美しいですね。

サンプルコード

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

import mglearn

X, y =mglearn.datasets.make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

lr = LinearRegression().fit(X_train, y_train)

print("lr.coef_(傾きOR重み) : {}".format(lr.coef_))
print("lr.intercept_(切片) : {}".format(lr.intercept_))

print("Training set score: {:.2f}".format(lr.score(X_train, y_train)))
print("test set score: {:.2f}".format(lr.score(X_test, y_test)))

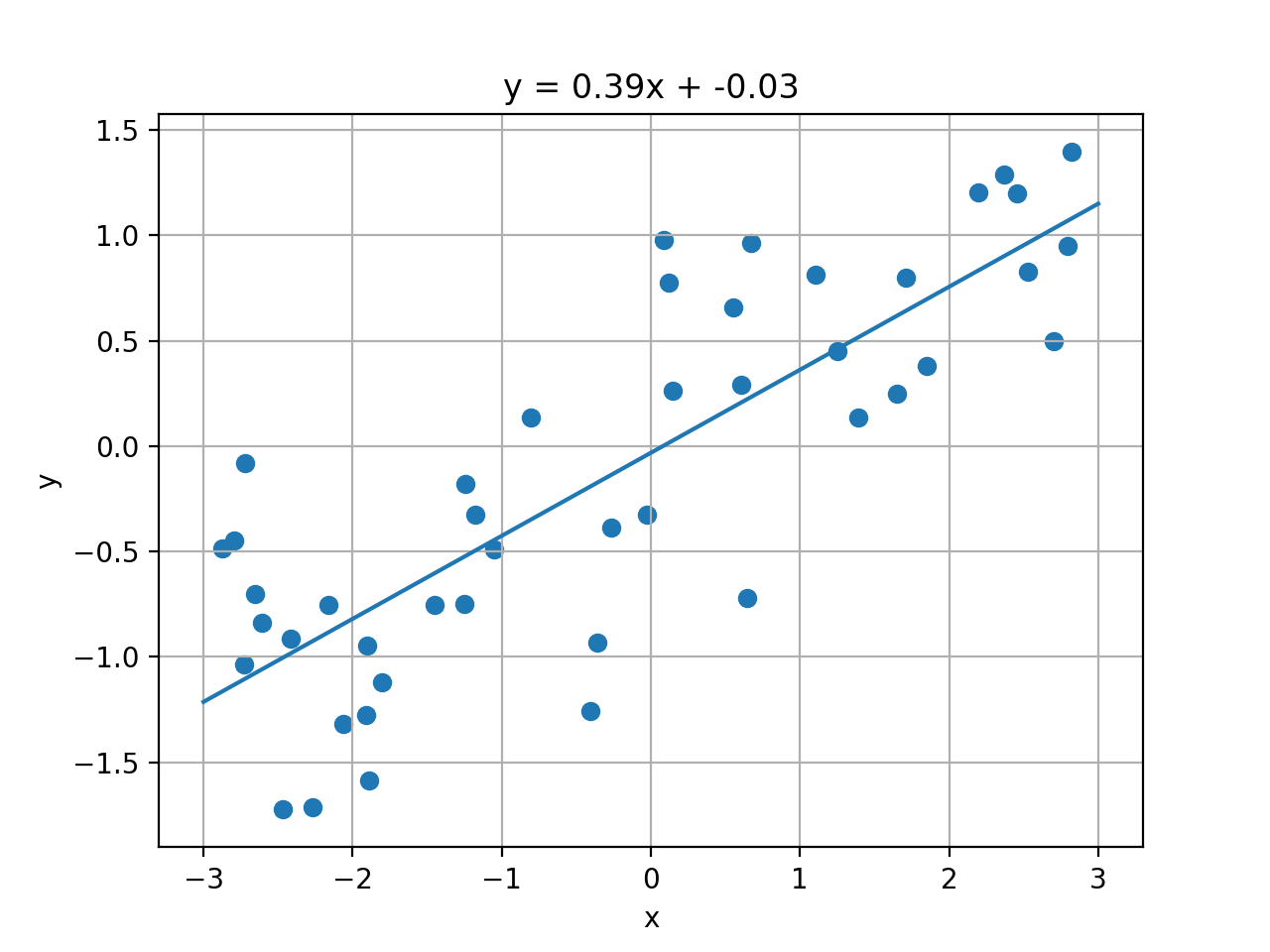
結果はこちら

lr.coef_(傾きOR重み) : [0.39390555]
lr.intercept_(切片) : -0.031804343026759746
Training set score: 0.67
test set score: 0.66

この直線をプロットしてみる。

しかし、予測が６６％とはあまり良くありませんね。
おそらくこれは適合不足（underfitting)だと考えられます。

次回は別の回帰モデルであるRidgeとLassoについてです。
皆さん、いい夜をお過ごしください。
おやすみなさい。