概要を読んでいない方は先にこちらを読んでください!
目次のページ
はじめに
今回は上図のcsv_path_dataの部分について説明します.
ロボットの経路生成には最適制御を用いました.様々な制約を考慮しつつ,評価関数を最小化することで設定した目的を達成できるためです.また,得られた最適経路情報はcsvファイルに保存しました.今回は最適制御による経路を事前にオフラインで保存するため,計算時間を考える必要がなかったので,特にモデル化において線形化などを行わず非線形最適制御問題を解きました.
最適制御とは
ある連続時間システム $\dot{x}(t) = f(x(t), u(t), t)$ を考えます.
そのとき,最適制御問題は以下のように定式化されます.
$\min \hspace{5pt}
J = \int^{T}_{0} L\left({x}\left(t\right), {u}\left(t\right), t\right) d\tau$
$\rm{s.t.}$ $\hspace{1pt} \dot{{x}}(t) = f({x}(t), {u}(t), t)$
$\hspace{30pt} g({x}(t), {u}(t), t) = 0$
$\hspace{30pt} h({x}(t), {u}(t), t) \leq 0$
車両制御への応用
今回は,コンテストで用いる(予定だった)車両ロボットTURTLEBOT3 Burgerに対して最適制御問題を解きます.
車両の座標を($x$,$y$),角度を$\theta$,車両への速度入力を$v$,角速度入力を$\omega$とします.すると,車両モデルの状態方程式は,状態ベクトルを $\boldsymbol{x}=\left[x,y,\theta\right]^\top$, 入力ベクトルを$\boldsymbol{u}=\left[v, \omega\right]^\top$とおくと,
$$
\dot{\boldsymbol{x}}=\frac{d}{d t}\left[\begin{array}{c}x, y, \theta\end{array}\right]^\top =\left[\begin{array}{c}v\cos\theta,v\sin\theta, \omega \ \end{array}\right]^\top
$$
と表されます.
そして,始点から終点まで最短で移動したいので,移動時間を最小化する問題を考えます.また,角速度の急激な変化は好ましくないため,角速度の分散も評価関数に加えました.
したがって,今回の問題設定において最適制御問題は以下のように定式化されます.
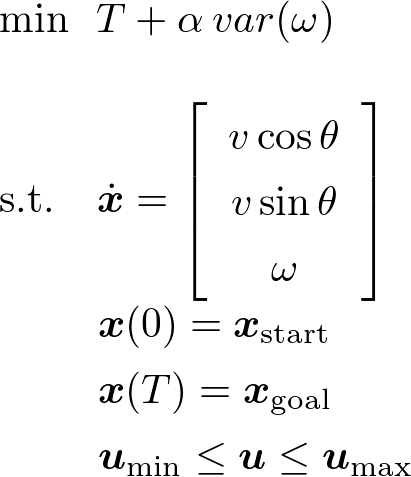
これを解くために,十分大きい$N$を用いて以下のように離散化します.

また,今回は自動微分・最適化ライブラリCasADiを用いてこの非線形最適制御問題を解きました.
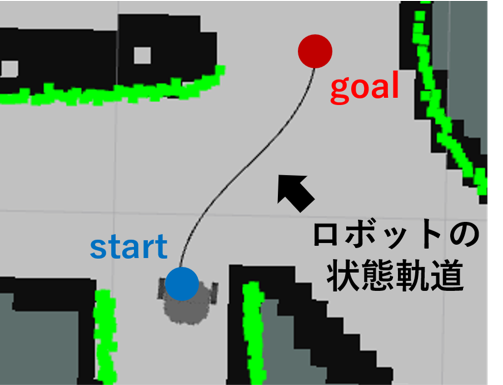
その結果を下に示します.
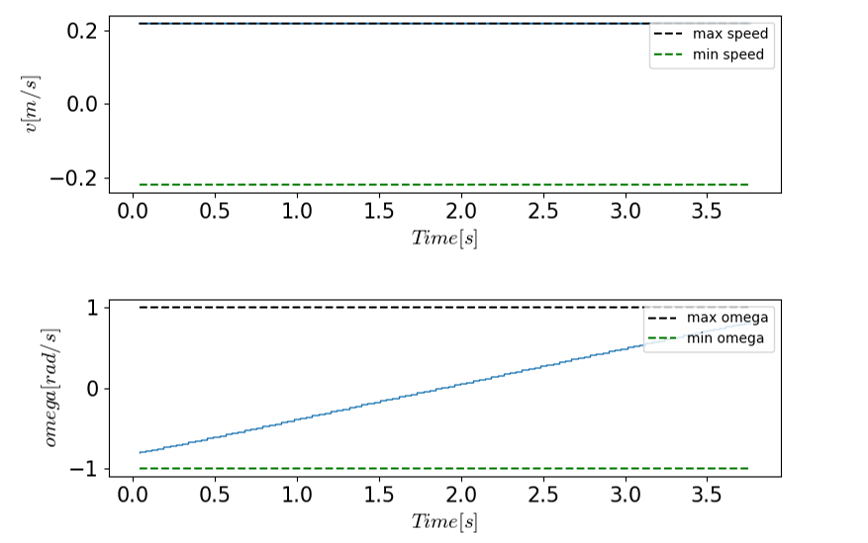
状態軌道が滑らかで,拘束条件を守りつつ,移動時間と角速度の分散を最小化していることがわかります.
ロボットの状態軌道
ロボットの速度入力と角速度入力の系列
参考文献
- 大塚敏之,非線形最適制御入門 コロナ社,2011.
- https://web.casadi.org/