0. はじめに
本稿では、量子機械学習のフレームワークであるQuantum Circuit Learning(K. Mitarai et al. 2019)を紹介します。この論文は少々古いですが、量子機械学習のエッセンスが詰まっています。
元の論文に加えて、筆者らのHPを参考にしました。以下が参考文献です。
[1] 元論文 https://arxiv.org/pdf/1803.00745.pdf
[2] 筆者らの実装記事 https://dojo.qulacs.org/ja/latest/notebooks/5.2_Quantum_Circuit_Learning.html
[3] 量子ゲートの代数表現を参考にした https://utokyo-icepp.github.io/qc-workbook/dynamics_simulation.html
筆者らは独自のシミュレータであるQulacsを使用していますが、本稿ではIBMのQiskitを使用します。
1. 仕組み
まず、量子回路の構成を俯瞰し、その後学習アルゴリズムを説明します。
これ以降、nはqubitの数を表します。
1.1 回路の構成
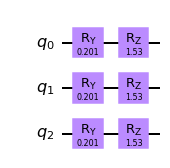
3つのコンポーネントで構成されます。1つ目は入力データをエンコードし、2つ目はqubitを相互に干渉させ、3つ目はパラメータに応じた回転ゲートを作用させます。
1.1.1 入力データのエンコーディング
適当にデータを角度エンコーディングします。実装ではデータ$x$を$R_{y}(\arcsin(x)),R_{z}(\arccos(x^2))$を用いて以下のように角度エンコーディングさせています(例はn=3の場合です)。
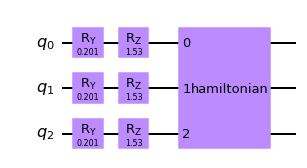
1.1.2 ランダムハミルトニアンによる干渉
作用させるハミルトニアンを$H = \sum_{i<j}Z_iZ_j+\sum_{i} X_{i}$と定義します。$X,Z$はパウリオペレータです。添え字は、作用するqubitの位置を表します。私は勘違いしていましたが、この式に出てくるパウリ行列は通常の$2×2$の行列ではなく、$2^n×2^n$の行列です。たとえば、3つのqubitで1番目と2番目に作用する行列を正確に書くと$Z_{1}\otimes Z_{2}\otimes I$で、これは$8×8$のエルミート行列です。
シュレーディンガー方程式を解くと$\exp(-iHt)$が得られ、これはユニタリ行列です。(エルミート行列の指数はユニタリ行列であるため)tは時間を表しこの実装では適当な定数が与えられます。
参考ページでは対角化して実装していますが、この文書では、qiskitのハミルトニアンから直接$\exp(-iHt)$をゲートとして実装できる関数を使用しています。$\exp(-iHt)$をそのまま行列としゲートに埋め込んでいるため(おそらく3-qubit程度なのでできた?)、qiskitではその詳細は表示されないようです。
ここで中身がどのように相互作用しているかを考えます。元のハミルトニアンは行列の指数であるため、$\exp(a+b) = \exp(a)\exp(b)$は一般的には成立しません。そこで、鈴木・トロッター分解なるものを行うことで、大きな数$M$(トロッタ数)を用いて$H$を$\left( \prod_{i<j} \exp(-itZ_{i}Z_{j}/M)\prod_{i} \exp(-itX_{i}/M) \right)^M$と近似することができます。$\exp(-itZ_{i}Z_{j}/M)$は、一般的に$CNOT_{ij}R_{z}(2*t/M)j CNOT_{ij}$となることが知られています(参考:[3]や筆者らの元記事のhttps://dojo.qulacs.org/ja/latest/notebooks/4.2_trotter_decomposition.html の下の方)。つまり、上記の図中の2つ目のコンポーネントは、近似して中身を見てみると、2量子ビットに作用するユニタリ変換の積となっていると言えます。
1.1.3 回転角をパラメータとしたゲートで回転させる
最後のコンポーネントは、パラメータ付きの回転ゲートで構成されます。このパラメータを学習誤差が小さくなるように学習します。$i$番目のビットに対して、$R_{x,i}(θ_{i,1})R_{z,i}(θ_{i,2})R_{z,i}(θ_{i,3})$と定義します。$n=3$の場合、$\prod_{i=1}^{3} R_{x,i}(θ_{i,1})R_{z,i}(θ_{i,2})R_{z,i}(θ_{i,3})$となります。各回転ゲートも$2×2$ではなく、$2^n×2^n$の行列です。この時点で最適化すべきパラメータ数は$3×n$であることがわかります。
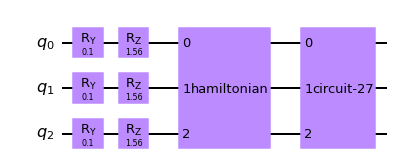
1.1.4 コンポーネントを繰り返す
元論文の筆者らの実装をまねして、エンコーディング以外の2つのコンポーネント群が3回繰り返されるようにします。そして1番上のビットのz方向の値を観測するために、その値を格納する古典レジスタを用意して、
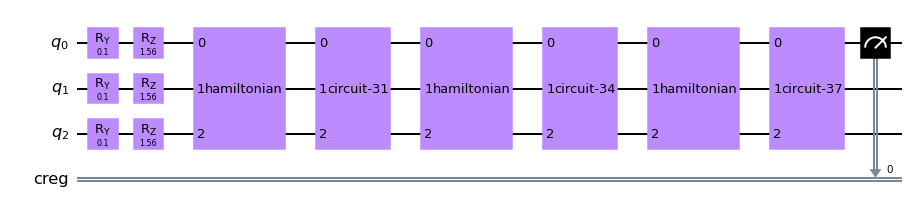
とします。これで完成です。最適化するために動かすパラメータは$3×3×3=27$です。
1.2 学習
1.2.1 誤差関数
$Z$測定で一番上のbitの$Z$方向の物理量の期待値を$\hat{y}$とし、この値と教師データ$y$の2乗誤差を小さくするようにパラメータを学習します。$-1≤E[Z]≤1$であるので、一般的なデータの値に対応するために、$\hat{y}$に定数倍$a$を乗じ($-a≤E[Z]≤a$となる)、この$a$も学習します。
今回は学習データが$sin$関数なので$a$はパラメータではなく定数を与えます。$-1≤sinx≤1$なので$a=1$で良いと思うのですが、参考ページでは$a=2$を与えています。実際$a=1$だと学習が上手くいきません($y=-1,1$付近で誤差が大きいまま学習が終わってしまう)。学習が上手くいくようにヒューリスティックに定めた値なのでしょう。私は$2$でもうまくいかなかったので$2.5$で設定しました。
1.2.2 学習アルゴリズム
- 2乗誤差の最小化のために古典の勾配フリーソルバーを使用します。ただし元の論文ではパラメータθの微分を計算する方法が提示されています。ご興味ある方はそちらを参照願います。
2. 実装
python上で実行可能なIBMのqiskitで実装します。qubit=3、コンポーネントの繰り返しも3で行います。設定部分など[2]の記事のコードをそのまま使わせて頂いています。
# 必要ライブラリのインストール
import numpy as np
from qiskit import *
import matplotlib.pyplot as plt
from qiskit.quantum_info.operators import Operator
from qiskit import Aer
from qiskit.quantum_info.operators import Operator, Pauli
from qiskit.extensions import HamiltonianGate # Hからexp(-itH)を計算
# 最適化計算のため
from scipy.optimize import minimize
使用するqubit数や、コンポーネントの繰り返し数を設定します。また学習するサンプルデータを作成します。ここでは$\sin(x)$但し$(-1≤x≤1)$を学習します。定義域を$(-1≤x≤1)$としているのは、エンコーディング角度を入力の逆三角関数としているからです。より一般の定義域を持つ関数の場合、入力を適当な値でスケールすれば良さそうです。
# パラメータ設定
nqubit = 3 # qubitの数
c_depth = 3 # circuitの深さ
time_step = 0.77 # ハミルトニアンによる時間発展の経過時間
# [x_min, x_max]のうち, ランダムにnum_x_train個の点をとって教師データとする.
x_min = - 1.; x_max = 1.;
num_x_train = 50
# 学習したい1変数関数
func_to_learn = lambda x: np.sin(x*np.pi)
# 乱数シード設定
np.random.seed(0)
# 教師データ
x_train = x_min + (x_max - x_min) * np.random.rand(num_x_train)
y_train = func_to_learn(x_train)
# 現実のデータを用いる場合を想定し、きれいなsin関数にノイズを付加
mag_noise = 0.1 # 参考先よりやや大きいばらつきとする
y_train = y_train + mag_noise * np.random.randn(num_x_train)
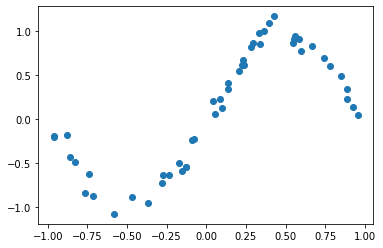
plt.plot(x_train, y_train, "o")# ; plt.show()
# xをエンコードするゲートを作成する関数
def U_in(x):
cirq = QuantumCircuit(nqubit)
angle_y = np.arcsin(x)
angle_z = np.arccos(x**2)
for i in range(nqubit):
cirq.ry(angle_y, i)
cirq.rz(angle_z, i)
return cirq
ハミルトニアン部分を作成します。
# ハミルトニアンの部分を作成
np.random.seed(0)
ham = Operator(np.zeros((2**nqubit, 2**nqubit)))
# l = []
for i in range(nqubit):
init_x = list('I'*nqubit) # Xはnqubit通り 全部単位行列で初期化 I⊗I⊗I
init_x[i] = 'X' # i番目だけXに変える I⊗X⊗I
print ("".join(init_x))
jx = -1. + 2.* np.random.rand() # ランダム磁場
# print (jx)
ham += jx * Operator.from_label("".join(init_x))
for j in range(i+1, nqubit): # Zはnqubit_C_2通り
init_z = list('I'*nqubit) # 全部単位行列で初期化 I⊗I⊗I
# print (i, j)
init_z[i] = 'Z' # i番目Z
init_z[j] = 'Z' # j番目Z Z⊗Z⊗I
print ("".join(init_z))
J_ij = -1. + 2.* np.random.rand() # ランダム相互作用
#print (J_ij)
ham += J_ij * Operator.from_label("".join(init_z))
# H→exp(itH)
gate = HamiltonianGate(ham, time_step)
回転ゲートも合わせて作成し、コンポーネント群を3回繰り返す関数を作成します。ハミルトニアン部分だけ関数ではなく、上記で作成したオブジェクトを使います(特に入力がないため)。
# パラメータを初期化
params_init = 2.0 * np.pi * np.random.rand(c_depth*nqubit*3)
# 入力x_iからモデルの予測値y(x_i, theta)を返す関数
def qcl_pred(x, params):
# 入力状態計算
circ = U_in(x)
# 出力状態計算
for k in range(c_depth): # c_depth回繰り返す
circ.append(gate, range(nqubit)) # あらかじめ定義しておいたハミルトニアンgate
# 回転ゲート作成
qc = QuantumCircuit(nqubit) # nqubitの回路作成
pmt = params.reshape(c_depth, nqubit ,3) # c_depth×nqubit×3のパラメータ配列
for i in range(nqubit):
qc.rx(pmt[k,i,0], i)
qc.rz(pmt[k,i,1], i)
qc.rx(pmt[k,i,2], i)
circ.append(qc, range(nqubit))
# 古典レジスタ
cr = ClassicalRegister(1,'creg')
circ.add_register(cr)
circ.measure(0,0) # 0番目の状態をz方向に観測
# モデルの出力
emulator = Aer.get_backend('qasm_simulator')
job = execute(circ, emulator, shots=1024 ) # 1024回観測
hist = job.result().get_counts()
# print (hist)
# z方向の期待値計算
if len(hist.keys())==2: # 0(or1)が100%の場合だけ処理かえる 要領悪いが...
res = (1 * hist['0'] -1 * hist['1']) / (hist['0'] + hist['1'])
else:
res = ((int(list(hist.keys())[0])+1) % 2)*2-1
# print (res)
res = 2.5 * res # この2.5倍はヒューリスティックであるが重要
return res
optimizeに与える目的関数(2乗誤差関数)を定義します。
# cost function Lを計算
def cost_func(params):
# num_x_train個のデータについて計算
y_pred = [qcl_pred(x, params) for x in x_train]
# quadratic loss
L = ((y_pred - y_train)**2).mean()
return L
scipyのoptimizeソルバーで解きます。
%%time
# 学習 2時間程度
opt_result = minimize(cost_func, params_init, method='Nelder-Mead')
学習したパラメータで$\sin$を再現できているか確認しましょう!
# パラメータthetaの初期値のもとでのグラフ
xlist = np.arange(x_min, x_max, 0.02)
y_init = [qcl_pred(x, params_init) for x in xlist]
plt.plot(xlist, y_init)
xlist = np.arange(x_min, x_max, 0.02)
y_init = [qcl_pred(x, opt_result.x) for x in xlist]
plt.plot(xlist, y_init)
plt.plot(x_train, y_train, "o")# ; plt.show()
# plt.plot(x,y)
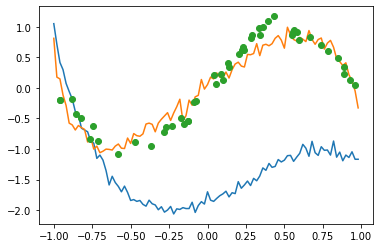
青色の線が初期値で、オレンジの線が学習後のパラメータで描画したものです。$y=-1,1$に近いところでの誤差が依然として残っていますが、まあまあいい感じです。
3. 考察など
驚くべきは、入力50事例に対して27個ものパラメータを用いていながら、過剰な適合をしていないところです。しかしこれを非効率(多くのパラメータが必要)とみるか、汎化性能が高いとみるかは議論が残ります。
入力事例1つにつき量子回路を作成する必要があります。そのため量子重ね合わせの計算の利点が失わているとも言えます。この問題は他の量子回路機械学習にみられる問題です。
今度はクラス分類にも挑戦したいです。では!