はじめに
Pythonで動かして学ぶ! あたらしいベイズ統計の教科書を読んだ事をgoogle colaboratryでやろうと思ったらこちらの記事にあるように、colabではpymc3ではなくpymcを使ってくれとのことなので、pymcでやってみました。
ベイズ推定とは
ベイズ推定は、統計的な手法の1つであり、事前に与えられた確率分布(事前分布)とデータを元に、事後分布を計算し、その分布を利用してパラメータの推定や予測を行う手法です。
ベイズ推定では、あるパラメータ(例えば、母平均や母分散など)が持つ確率分布を事前分布として仮定します。この事前分布は、事前にパラメータについて知っている情報や仮定に基づいて設定されます。そして、データが得られた後、データと事前分布を組み合わせて事後分布を計算し、それによりパラメータの推定や予測が可能になります。
ベイズ推定に使用するデータの取得と前処理
今回も、私の以前書いた記事で使用したScikit-learnのデータセットのボストン市の住宅価格を使おうと思ったら、こいつもScikit-learnの最新バージョンじゃdeprecatedになってるじゃん...、仕方ないので、同じScikit-learnのデータセットにある糖尿病患者の診療データセットを使用したいと思います。糖尿病患者の診療データセットは、糖尿病患者の検査数値と1年後の進行状況をデータセットにしたものです。
まずは、データ取得と前処理に使うライブラリのインポート
import numpy as np
import pandas as pd
from sklearn.datasets import load_diabetes
そしてデータの読み込み
diabetes = load_diabetes()
diabetes_data = pd.DataFrame(diabetes.data, columns = diabetes.feature_names).assign(target=np.array(diabetes.target))
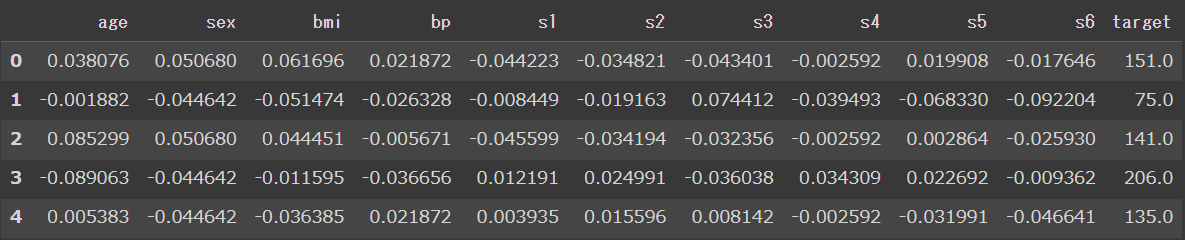
せっかくなので、データの中身と概要も見ておきましょう。
diabetes_data.head()
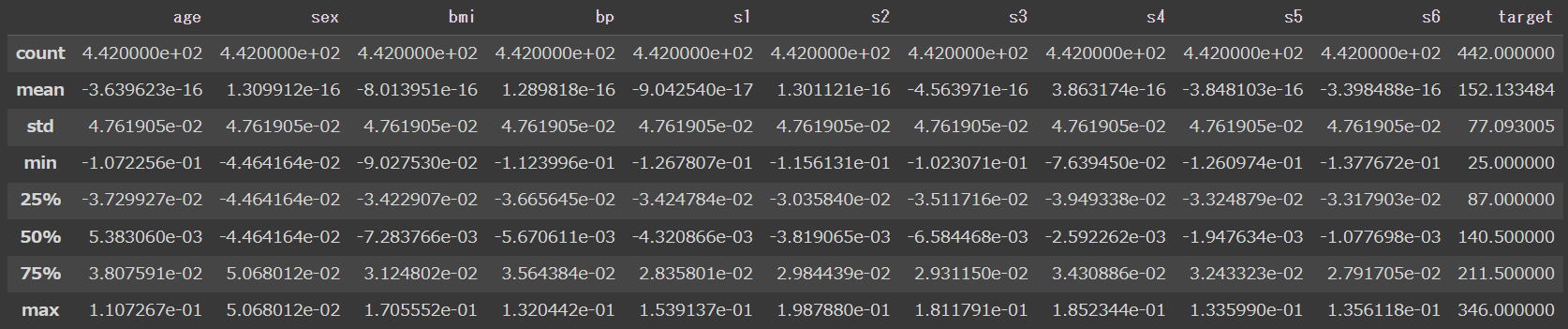
diabetes_data.describe()
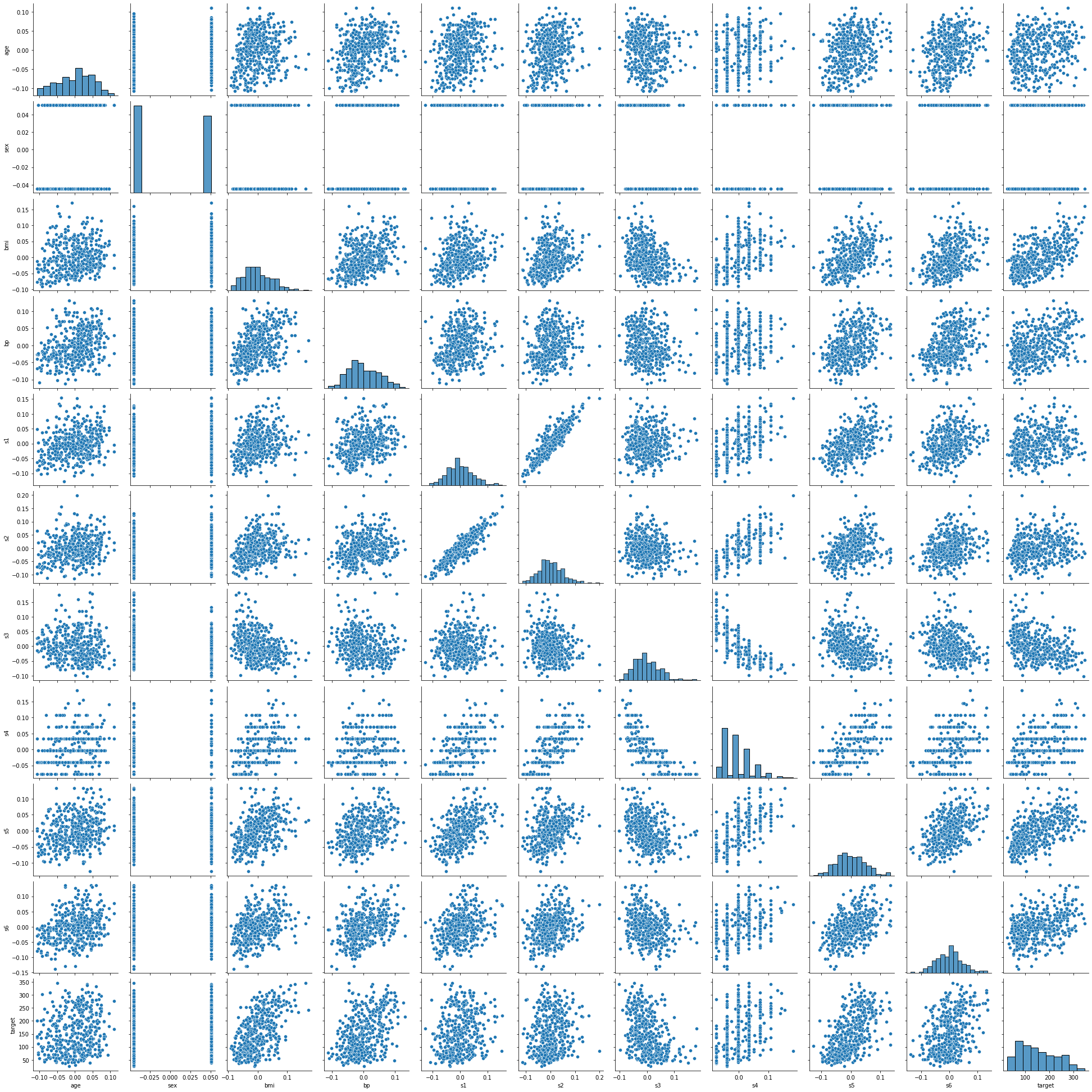
seabornのpairplotを使ってデータの関係性も見ておきましょう。
import seaborn as sns
sns.pairplot(diabetes_data)
とりあえずこの中で、s1(tc、総血清コレステロール)とs2(ldl、低密度リポタンパク質)が高い相関関係を持ってそうなので、それを使って単回帰分析を行います。
X = diabetes_data[['s1']].values
y = diabetes_data[['s2']].values
Scikit-learnを使った単回帰分析
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(X, y)
y_pred = reg.predict(X)
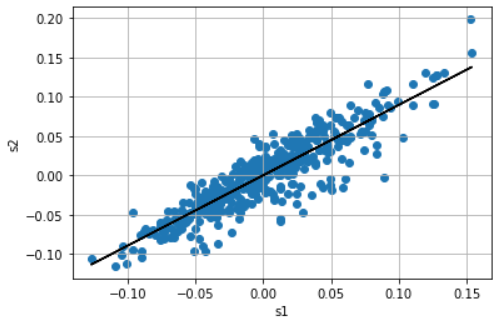
回帰直線の描画、単回帰分析なのでy=α+βXで表せます。
import matplotlib.pyplot as plt
plt.scatter(X, y)
plt.plot(X, reg.predict(X), color='black')
plt.xlabel('s1')
plt.ylabel('s2')
plt.grid()
plt.show()
Scikit-learnによる単回帰分析で求めた回帰直線の切片(alpha_0)と傾き(beta_0)を表示
alpha_0 = reg.intercept_[0]
beta_0 = reg.coef_[0][0]
print("alpha_0:", alpha_0)
print("beta_0:", beta_0)
出力
alpha_0: 5.1571733982230335e-17
beta_0: 0.8966629578104912
pymcを使ったベイズ推定による線形回帰
それでは、ここからが本題のpymcを使ったベイズ推定による線形回帰になります。
pymcをインポートしてから、取得したデータを、切片(α)、傾き(β)の事前分布が平均0、標準偏差10の正規分布、観測値の標準偏差が半正規分布の線形回帰モデルを定義します。
import pymc as pm
with pm.Model() as model:
alpha = pm.Normal("alpha", mu=0, sigma=10) #切片
beta = pm.Normal("beta", mu=0, sigma=10) #傾き
sigma = pm.HalfNormal("sigma", sigma=1) #データのばらつき
mu = alpha + beta * X
Y_obs = pm.Normal("Y_obs", mu=mu, sigma=sigma, observed=y)
sample関数を用いて事後分布のサンプリング
with model:
trace = pm.sample()
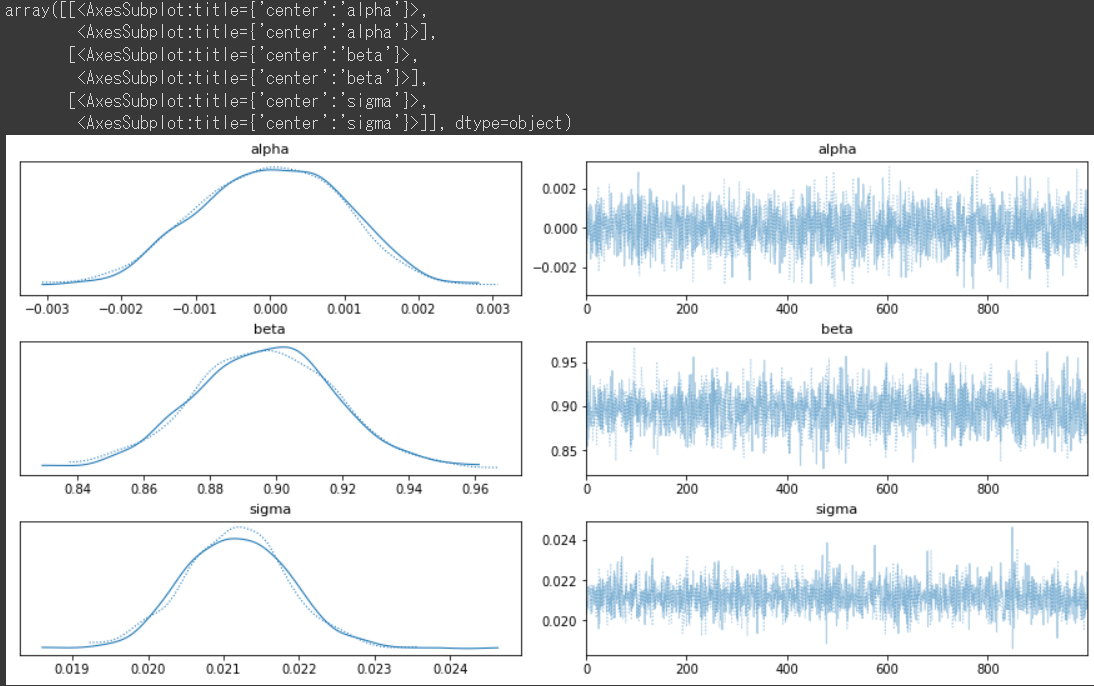
plot_trace関数を用いて結果を可視化
var_names = ["alpha", "beta", "sigma"]
pm.plot_trace(trace, var_names=var_names, backend_kwargs={"constrained_layout":True})
summary関数で要約統計量を表示。結果からScikit-learnによる単回帰分析で求めた回帰直線の切片と傾きとほぼ同じであることが確認できました。
pm.summary(trace, var_names=var_names)
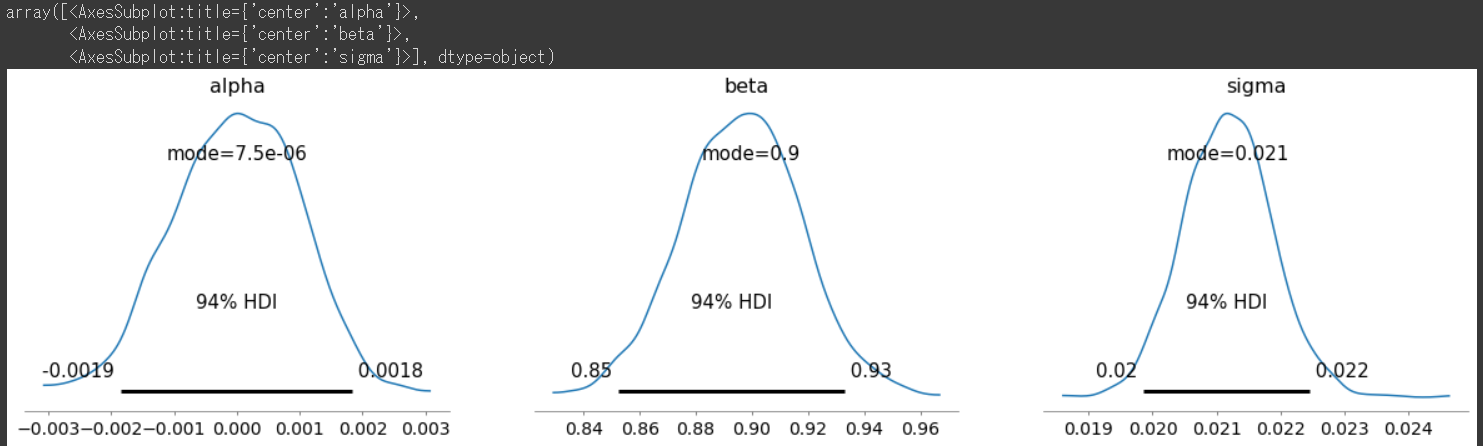
plot_posterior関数で推論された事後分布と信頼区間を表示。
pm.plot_posterior(trace, point_estimate='mode')
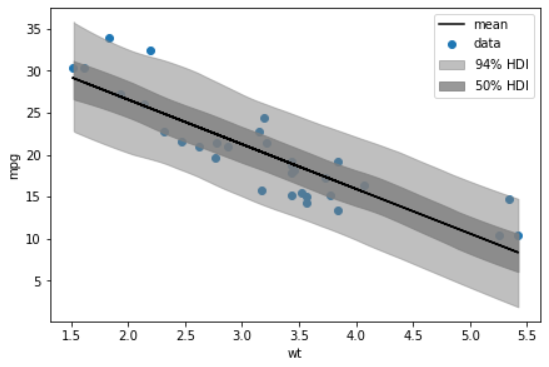
おわりに
本当は以下みたいな感じの線形回帰のグラフに信頼区間も表示したかったのですが、pymc3からpymcに変えた影響もあってか、上手くできませんでした。機会があればまた挑戦したいと思います。