二項分布とは
二項分布(Binomial Distribution)とは、互いに独立したベルヌーイ試行をn回行ったときに、ある事象が何回起こるかの確率分布です。例えば、「コインを5回投げた時に表2回出る確率」「SRの出現割合が1%のガチャを100回まわして1回SRを引ける確率」などを表した確率分布です。
※ベルヌーイ試行・・・「成功か失敗か」「表か裏か」「勝ちか負けか」のように2種類のみの結果しか得られないような実験、試行のこと
二項分布は科学技術計算でよく使われるライブラリSciPyにあるstatsを使用して計算することができます。
確率50%のコインを10回投げて表が出る確率の二項分布の例
まずは簡単に例題としてコインを10回投げた時の表の出る確率の二項分布を表示してみます。pは確率、nは試行回数を入力します。
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
plt.style.use("seaborn-darkgrid")
n = 10 #試行回数
p = 0.5 #確率
x = np.arange(n + 1)
plt.bar(x, stats.binom.pmf(x, n, p))
plt.xlabel('number of successes')
plt.ylabel('probability')
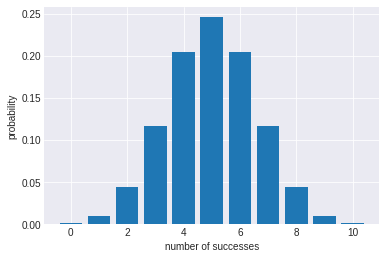
出力結果
このグラフでは、5回ほど表が確率が最も高くだいたい25%、そして9回、11回ほど表が出る確率が同じくらいで約20%ということがわかります。
確率1%の当たりのガチャを100回まわした確率の二項分布の例
そして上記のコードのnとpの値を変えれば、確率1%(p=0.01)のガチャを100回(n=100)まわした時に当たりが何回出るかをグラフ化することができます。
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
plt.style.use("seaborn-darkgrid")
n = 100 #試行回数
p = 0.01 #確率
x = np.arange(n + 1)
plt.bar(x, stats.binom.pmf(x, n, p))
plt.xlim(-1, 10) #X軸の表示範囲を指定
plt.xlabel('number of successes')
plt.ylabel('probability')
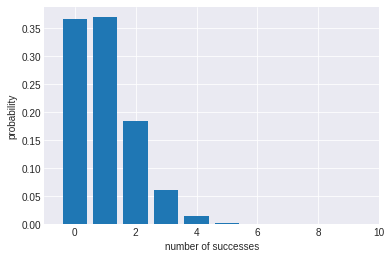
出力結果
グラフから確率1%のガチャを100回まわした場合、1回当たりが出る確率はだいたい36%程度で、0回もほぼ同じ確率ということがわかります。
確率1%の当たりのガチャを100回、200回、300回とまわしてみた場合の比較
それでは上記のコードに少し手を加えて最後に確率1%の当たりのガチャを100回、200回、300回とまわしてみた場合の二項分布を比較をしてみたいと思います。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
plt.style.use("seaborn-darkgrid")
def show_binom(x, n, p):
plt.bar(x, stats.binom.pmf(x, n, p), alpha=0.5, label=r"$N$:"+str(n))
p = 0.01 #確率
n = 100 #試行回数
x = np.arange(n + 1)
show_binom(x, n, p)
n = 200 #試行回数
x = np.arange(n + 1)
show_binom(x, n, p)
n = 300 #試行回数
x = np.arange(n + 1)
show_binom(x, n, p)
plt.xlim(-1, 12) #X軸の表示範囲を指定
plt.xlabel('number of successes')
plt.ylabel('probability')
plt.legend()
plt.show()
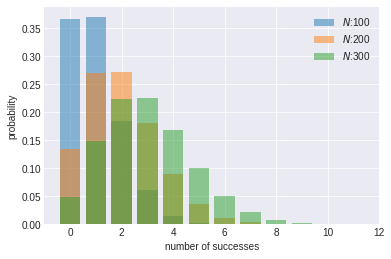
出力結果
この結果を見ると、当たりの確率1%のガチャを300回まわしても、5%ぐらいの確率で当たりが出ないということがわかりますね。
まとめ
ガチャってやっぱり怖いね。