zkSNARKs全然理解できないので一度まとめてみる.
zkSNARKs とは
zkSNARK (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge)
- Zero-Knowledge: ある命題が真であることを証明する際に,それ以外の情報を外部に漏らさなくて良い
- Succinct: 証明のサイズが非常に小さく迅速な検証が可能である
- Non-interactive: 証明者と検証者間で対話をする必要が無い
結局何が出来るの?
証明者は検証者に$y=f(x)$が成り立つことを証明したいとします.率直に考えれば$x, y, f$を検証者に渡し,実際に計算してもらうのが一番簡単でしょう.しかし,$x$が例えば個人情報など秘密にしたい値だった場合この方法は使えません.ここでzkSNARKsの登場です.zkSNARKsを使用すると$x$を秘密にしたまま$y=f(x)$が成り立つことを証明でき,更に実際に計算して確かめるよりも少ない時間で検証が可能になります.
zkSNARKsの手順
以下,$f(x)=x^3+x+5$を例に考えていきます.ここでは,$f(x)$の解$(x=3)$を知っていることを,その解の情報を公開することなく検証者に証明します.
問題(方程式)をQAPへ
まずはじめに,zkSNARKsを適用するため,問題をQAPと呼ばれる形式に変換します.以下順を追って説明していきます.
方程式から算術回路へ
まず,$y=f(x)$を平坦化します.具体的には,$y=f(x)$を$a=b (op) c$の集まりに分解します.$(op)$は演算子を表し,今回は $+,*$ が入ります.以下が,$f(x)=x^3+x+5$を平坦化した式であり,元の式関係を保ちながら四つの式に分解されていることが分かります.
\displaylines{
\begin{align}
&G_1: \quad \mu_1=x * x \\
&G_2: \quad \mu_2=\mu_1 * x \\
&G_3: \quad \mu_3=\mu_2 + x \\
&G_4: \quad out=\mu_3 + 5
\end{align}
}
この平坦化された式のそれぞれは2入力1出力のゲート$G_i$と考えることができ,それらの集まりは算術回路として考えることが出来ます.
算術回路からR1CSへ
次に,算術回路をR1CS(Rank-1 Constraint System)に変換します.R1CSでは,算術回路で表される関係を保ちながら以下の等式を満たすような行列$A, B, C$を計算により求めます.$\star$演算子は行列の要素同士の掛け算を意味します.解ベクトル$\boldsymbol{a}$は式の変数と,定数を表すために必要な$1$から構成されます.
\boldsymbol{a}=(one, x, out, \mu_1, \mu_2, \mu_3)^T
(A\cdot\boldsymbol{a})\star(B\cdot\boldsymbol{a})=C\cdot\boldsymbol{a}
今回の例では,以下の行列$A, B, C$が等式を満たします.
A=\begin{pmatrix}
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 \\
0 & 1 & 0 & 0 & 1 & 0 \\
5 & 0 & 0 & 0 & 0 & 1 \\
\end{pmatrix},
B=\begin{pmatrix}
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 \\
\end{pmatrix},
C=\begin{pmatrix}
0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 & 0 & 0 \\
\end{pmatrix}
本当に満たしているかの確認
一つずつ確認していきます.まず一行目.
\displaylines{
\begin{pmatrix}
0 & 1 & 0 & 0 & 0 & 0
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}\star
\begin{pmatrix}
0 & 1 & 0 & 0 & 0 & 0
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}=
\begin{pmatrix}
0 & 0 & 0 & 1 & 0 & 0
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}
\\
\Leftrightarrow
x * x = \mu_1
}
計算結果が算術回路の一つ目と等しくなることが分かります.
同様にして二行目.
\displaylines{
\begin{pmatrix}
0 & 0 & 0 & 1 & 0 & 0
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}\star
\begin{pmatrix}
0 & 1 & 0 & 0 & 0 & 0
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}=
\begin{pmatrix}
0 & 0 & 0 & 0 & 1 & 0
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}
\\
\Leftrightarrow
\mu_1 * x = \mu_2
}
三行目.先ほどとは違い$+$演算が出てきます.この場合,左辺の$\star$演算左側で$+$演算を行い,$\star$演算右側は$one$にして$\star$演算で定数$1$を掛けるだけにします.
\displaylines{
\begin{pmatrix}
0 & 1 & 0 & 0 & 1 & 0
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}\star
\begin{pmatrix}
1 & 0 & 0 & 0 & 0 & 0
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}=
\begin{pmatrix}
0 & 0 & 0 & 0 & 0 & 1
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}
\\
\Leftrightarrow
(x + \mu_2) * one = \mu_3
\\
\Leftrightarrow
x + \mu_2 = \mu_3
}
最後に四行目.これも三行目の例と同様です.
\displaylines{
\begin{pmatrix}
5 & 0 & 0 & 0 & 0 & 1
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}\star
\begin{pmatrix}
1 & 0 & 0 & 0 & 0 & 0
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}=
\begin{pmatrix}
0 & 0 & 1 & 0 & 0 & 0
\end{pmatrix}\cdot
\begin{pmatrix}
one \\ x \\ out \\ \mu_1 \\ \mu_2 \\ \mu_3
\end{pmatrix}
\\
\Leftrightarrow
(5 + \mu_3) * one = out
\\
\Leftrightarrow
5 + \mu_3 = out
}
よって,これらの行列$A, B, C$が算術回路を満たすことが分かりました.
\boldsymbol{a}=(1, 3, 35, 9, 27, 30)^T
解ベクトル$\boldsymbol{a}$の計算
\displaylines{
\begin{align}
(\mu_1=x * x)|_{x=3} \rightarrow 9&=3 *3 \\
(\mu_2=\mu_1 * x)|_{x=3} \rightarrow 27&=9 * 3 \\
(\mu_3=\mu_2 + x)|_{x=3} \rightarrow 30&=27 + 3 \\
(out=\mu_3 + 5)|_{x=3} \rightarrow 35&=30 + 5
\end{align}
}
R1CSからQAPへ
最後に,R1CSをQAP(Quadratic Arithmetic Program)に変換します.まず,先ほどの章で求めた行列 $A,B,C$ の列を多項式に変換します.具体的には,ある列($A$の一列目)の要素を$y$座標に,index:[1, 2, 3, 4] を$x$座標として$xy$座標面の点としてプロットします.
Aの一列目:
\begin{pmatrix}
0 \\ 0 \\ 0 \\ 5
\end{pmatrix}
=>
\{(1, 0), (2, 0), (3, 0), (4, 5)\}
次に,プロットした点を全て通るような多項式をラグランジュ補間で計算します.点がd個あると,d-1次の多項式が算出され,今回の例では3次多項式 $0.83x^3-5x^2+9.17x-5$ となります.
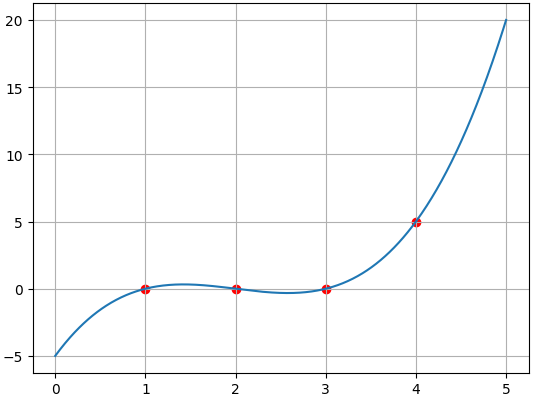
このように,行列 $A $ の$i$列目を多項式 $A_i$ で表現すると以下の様になります.行列 $B, C$ も同様です.
A=\begin{pmatrix}
A_1(1) & A_2(1) & A_3(1) & A_4(1) & A_5(1) & A_6(1) \\
A_1(2) & A_2(2) & A_3(2) & A_4(2) & A_5(2) & A_6(2) \\
A_1(3) & A_2(3) & A_3(3) & A_4(3) & A_5(3) & A_6(3) \\
A_1(4) & A_2(4) & A_3(4) & A_4(4) & A_5(4) & A_6(4) \\
\end{pmatrix}
多項式$A_i, B_i, C_i$
\displaylines{
\begin{align}
A_1(x) &= 0.833x^3 - 5.0x^2 + 9.166x - 5.0 \\
A_2(x) &= -0.666x^3 + 5.0x^2 - 11.333x + 8.0 \\
A_3(x) &= 0.0x^3 + 0.0x^2 + 0.0x + 0.0 \\
A_4(x) &= 0.5x^3 - 4.0x^2 + 9.5x - 6.0 \\
A_5(x) &= -0.5x^3 + 3.5x^2 - 7.0x + 4.0 \\
A_6(x) &= 0.166x^3 - 1.0x^2 + 1.833x - 1.0 \\
\end{align}
}
\displaylines{
\begin{align}
B_1(x) &= -0.333x^3 + 2.5x^2 - 5.166x + 3.0 \\
B_2(x) &= 0.333x^3 - 2.5x^2 + 5.166x - 2.0 \\
B_3(x) &= 0.0x^3 + 0.0x^2 + 0.0x + 0.0 \\
B_4(x) &= 0.0x^3 + 0.0x^2 + 0.0x + 0.0 \\
B_5(x) &= 0.0x^3 + 0.0x^2 + 0.0x + 0.0 \\
B_6(x) &= 0.0x^3 + 0.0x^2 + 0.0x + 0.0 \\
\end{align}
}
\displaylines{
\begin{align}
C_1(x) &= 0.0x^3 + 0.0x^2 + 0.0x + 0.0 \\
C_2(x) &= 0.0x^3 + 0.0x^2 + 0.0x + 0.0 \\
C_3(x) &= 0.166x^3 - 1.0x^2 + 1.833x - 1.0 \\
C_4(x) &= -0.166x^3 + 1.5x^2 - 4.333x + 4.0 \\
C_5(x) &= 0.5x^3 - 4.0x^2 + 9.5x - 6.0 \\
C_6(x) &= -0.5x^3 + 3.5x^2 - 7.0x + 4.0 \\
\end{align}
}
この多項式変換を適用すると,R1CSで定義された等式を多項式の計算に落とし込むことが出来ます.もちろん,この等式は間違った$a_i$の割り当てでは成り立ちません.
\sum^6_{i=1}a_iA_i(x)\sum^6_{i=1}a_iB_i(x)=\sum^6_{i=1}a_iC_i(x)
次に,おもむろに以下のような$p(x)$を考えます.
p(x)=\sum^6_{i=1}a_iA_i(x)\sum^6_{i=1}a_iB_i(x)-\sum^6_{i=1}a_iC_i(x)
この$p(x)$は$x=1,2,3,4$を根に持ちます.つまり,$t(x)=(x-1)(x-2)(x-3)(x-4)$とすると,$p(x)=t(x)h(x)$と分離できるはずです.
p(x)=\sum^6_{i=1}a_iA_i(x)\sum^6_{i=1}a_iB_i(x)-\sum^6_{i=1}a_iC_i(x) = t(x)h(x)
ここで,「解ベクトル$\boldsymbol{a}$の割り当てを知っていること」を「$p(x)/t(x)$が割り切れるような$h(x)$を知っている」という問題,つまりQAPに変換できました.
以下,$\sum^6_{i=1}a_iA_i(x)=A(x),\sum^6_{i=1}a_iB_i(x)=B(x),\sum^6_{i=1}a_iC_i(x)=C(x)$とします.
確認のため,$p(x)$を計算してみましょう.
\displaylines{
\begin{align}
A(x)&=-5.166x^3 + 38.5x^2 - 73.333x + 43.0 \\
B(x)&=0.666x^3 - 5.0x^2 + 10.333x - 3.0 \\
C(x)&=2.833x^3 - 24.5x^2 + 71.666x - 41.0 \\
\end{align}
}
p(x)=-3.444x^6 + 51.5x^5 - 294.777x^4 + 805.833x^3 - 1063.777x^2 + 592.666x - 88.0
$p(x)$のグラフを見ると,$x=1,2,3,4$の点で$p(x)=0$になっていることが分かります.

次に,以下のような間違った割り当て$a_i$を使用して$p(x)$を計算してみます.
a_i=[1, 3, 35, 9, 27, \color{red}{20}]
p(x)=-4.556x^6 + 66.5x^5 - 374.222x^4 + 1007.5x^3 - 1298.222x^2 + 681.0x - 78.0
$p(x)$を$x=1,2,3,4$で評価すると以下の様に$x=3,4$でゼロにならず不当な割り当てであることが分かります.もちろん$p(x)$を$t(x)$で割り切ることも出来ません.

ある$x$で$p(x)\ne0$とは,割り当てがそれに対応するゲートの制約を満たしていないという事です.$x=1,2,3,4$はそれぞれゲート$G_1,G_2,G_3,G_4$に対応します.したがって,制約を満たさない$x=3,4 (G_3,G_4)$において$p(x)\ne0$となっています.
\displaylines{
\begin{align}
&G_1: \quad (\mu_1=x * x) \rightarrow 9=3 *3 \\
&G_2: \quad (\mu_2=\mu_1 * x) \rightarrow 27=9 * 3 \\
&G_3: \quad (\mu_3=\mu_2 + x) \rightarrow \color{red}{20} \ne 27 + 3 \\
&G_4: \quad (out=\mu_3 + 5) \rightarrow 35\ne\color{red}{20} + 5
\end{align}
}
実際には全ての$x$でゼロになることを確認するのではなく,上にも示した通り$p(x)$が$t(x)$で割り切れるかどうかを確認します.今回の例ではゲートは四つでしたが,実際には数千~数万になります.このゲート全てを確認するのは非常に面倒ですが,QAPを使えば多項式の計算一回で全てのゲートを確認出来てしまいます.
一旦まとめ
ここまでの長い道のりでようやく問題をQAPに変換できました.単純に考えればzkSNARKsは既に機能しそうです.証明者は検証者に$A(x),B(x),C(x),h(x)$を送り,$(A(x)B(x)-C(x))=h(x)t(x)$を検証してもらえば良さそうな気がします.しかし,欠点があります.第一に,$t(x)$から$(A(x)B(x)-C(x))=t(x)h(x)$となるような$A(x),$$B(x)$$,C(x)$$,h(x)$を作れてしまう事.第二に,$A(x),B(x),C(x)$を形成する秘密にしたい割り当て$a_i$が検証者に公開されてしまう事です.
Pinocchioプロトコル
Pinocchioプロトコルとは,zkSNARKsを実現するために考案された非常にシンプルなプロトコルです.以下,重要な四つのテクニックについて説明します.
重要なテクニック
KEA (Knowledge of Exponent Assumption)
有限巡回群の生成元を$P$として$Q=P^k$を考えたとき,$Q$と$P$から$k$を求めることは非常に困難とされ,離散対数問題(DLP)と呼ばれます.更に,楕円曲線上では$Q=k * P$から$k$を求めることは非常に困難とされます(ECDLP)(正確な解説は他の記事に任せます).
唐突ですが,$k$が分からない状態から,$R=k * S$となるような$R$と$S$を作れるでしょうか.方法は唯一,線形結合を考えることです.$Q_n=k * P_n$となるような$n$個のペア$(P_n,Q_n)$があったとします.もちろん$k$は分かりません.ここで,以下の様に$R$と$S$を線形結合により形成すれば$R=k*S$となり条件を満たします.
\displaylines{
\begin{align}
S&=i_1*P_1+i_2*P_2+\cdots+i_n*P_n \\
R&=i_1*Q_1+i_2*Q_2+\cdots+i_n*Q_n
\end{align}
}
\displaylines{
\begin{align}
k*S &= i_1*k*P_1+i_2*k*P_2+\cdots+i_n*k*P_n \\
&= i_1*Q_1+i_2*Q_2+\cdots+i_n*Q_n \\
&= R
\end{align}
}
$Q_n=k*P_n$となるようなペアが少なくとも2個以上あれば,$k$を知らずに線形結合から$R=k * S$となるような$R$と$S$を作れることが分かりました.KEAではこれを利用し,$R$と$S$が線形結合で形成されていることを証明できます.
zkSNARKsではKEAを利用し,$A(x),B(x),C(c)$が線形結合で形成されていること,つまり$A(x)B(x)-C(x)=t(x)h(x)$となるように適当に作られた多項式では無いことを証明できます.
有限巡回群?楕円曲線?
この記事を読むために必要最低限の説明をします.
-
有限巡回群
常に$5$で割った余りを考える世界で$\lbrace 0,1,2,3,4 \rbrace$みたいな集合を考えたとき,これは加法に関して有限巡回群です.加法とは足し算です.元(要素)が五個しかないので有限です.$1+1=2,2+1=3,3+1=4,4+1=0$($5$で割るから)という風に$1$の演算だけで全ての元を表現できるので巡回です. -
楕円曲線
楕円曲線は以下のような関数です.y^2=x^3+ax+bこの曲線上の点に以下の様な演算を定義してみます.(図はWikipediaより)
\displaylines{ P+Q=-R \\ k * P = P+P+\cdots+P }このままでは何も起きませんが,有限体(群の仲間)上の楕円曲線を考えると不思議なことに,$Q=k * P$から$k$を求めることが出来なくなります(語弊あり).
正確な説明,定義は別のサイトをご確認ください.この説明がいかに適当か分かります.
Schwartz–Zippelの補題
体$\mathbb{F}_p$上の未知の$n$次多項式$f(x),g(x)$が同じかどうかを検証したいとします.これを確かめるには全ての$x$について$f(x)-g(x)=0$となるか検証しなければなりません.これは非常に面倒です.しかし,ランダムに選んだ$s$について$f(s)-g(s)=0$なら同じ,$f(s)-g(s)\ne0$なら異なると高い確率で判定できます.
理由は簡単で,$f(x) \ne g(x)$の場合,多項式$f(x)-g(x)$がもつ根は高々$n$個のため,体$\mathbb{F}_p$からたまたま$f(s)-g(s)=0$となるような$s$を選ぶ確率は$n / |\mathbb{F}_p|$となります.$p \gg n$の時この確率は非常に小さいため,ある一点$s$のみで$f(x),g(x)$が同じかどうかを検証出来ます.これがSchwartz–Zippelの補題です.
楕円曲線のペアリング
双線形性をもつ写像$e:G_1 \times G_2 \rightarrow G_3$をペアリングと呼びます($\times$は掛け算ではなく直積です).$G_1,G_2$はどちらも楕円曲線で,その座標は有限体$\mathbb{F}_p$上の要素です.$G_3$は拡大体として定義されます.また,双線形性とは以下のような性質です
\displaylines{
e(P+Q,R)=e(P,R) * e(Q,R) \\
e(P,Q+R)=e(P,Q) * e(P,R)
}
このような写像を考えたとき,以下が成り立ちます.つまり,楕円曲線上でのスカラー倍が拡大体上での累乗に結び付いています.
\displaylines{
e(aP,Q)=e(P,aQ)=e(P,Q)^a
}
ペアリングは非常に難しい数学です.実際私もほとんど理解できていません.しかし,ここではそういうものだと思って読み進めてください.
Pinocchioプロトコルの実装
上記に示した四つのテクニックを使用して,Pinocchioプロトコルを実装します.実装に際して,証明者,検証者のほかに信頼できる第三者が必要になります.今後単純に設定者と呼びます.まずはじめに,設定者がランダムな値$s,k_a,k_b,k_c$を決定し,以下の値を計算して公開します.この作業はTrusted Setupと呼ばれます.$G$及び計算された値は楕円曲線上の点です.楕円曲線上の離散対数問題より,$G * A_i(s) * k_a$から$A_i(s)$及び$k_a$を計算することは困難となっています.
\displaylines{
G * A_i(s), \quad G * A_i(s) * k_a \\
G * B_i(s), \quad G * B_i(s) * k_b \\
G * C_i(s), \quad G * C_i(s) * k_c
}
$s,k_a,k_b,k_c$はtoxic waste(有害廃棄物)と呼ばれ,計算後ただちに捨てなければなりません.次に,証明者は公開された値から以下の証明$\pi$を作成します.もちろん,証明者は$s,k_a,k_b,k_c$の値を知らずに計算できます.
\displaylines{
\pi_a=G * A(s), \quad \pi_a'=G * A(s) * k_a \\
\pi_b=G * B(s), \quad \pi_b'=G * B(s) * k_b \\
\pi_c=G * C(s), \quad \pi_c'=G * C(s) * k_c \\
}
証明の作成を見てみましょう.まず,$G * A_i(s)$から割り当て$a_i$を用いて$\pi_a$を作成します.
\displaylines{
\begin{align}
&a_1(G * A_1(s))+a_2(G * A_2(s))+ \cdots +a_n(G * A_n(s)) \\
&=G * (a_1A_1(s)+a_2A_2(s)+\cdots+a_nA_n(s)) \\
&=G * A(s) \\
&=\pi_a
\end{align}
}
楕円曲線上の演算$ * $とスカラー倍が混じっていて大丈夫なのか?と感じますが,$G * A_1(s)$は楕円曲線上の点$G$と数値$A_1(s)$の演算なので$ * $で計算.$a_1A_1(s)$は数値同士の計算なのでスカラー倍と考えれば良いと思います.
次に$G * A_i(s) * k_a$から割り当て$a_i$を用いて$\pi_a'$を作成します.
\displaylines{
\begin{align}
&a_1(G * A_1(s) * k_a)+a_2(G * A_2(s) * k_a)+ \cdots +a_n(G * A_n(s) * k_a) \\
&=G * (a_1A_1(s)+a_2A_2(s)+\cdots+a_nA_n(s)) * k_a \\
&=G * A(s) * k_a \\
&=\pi_a'
\end{align}
}
他の証明についても同様に作成すればよいです.結果,提出された証明と公開情報からKEAにより$A(s),B(s),C(s)$が線形結合で形成されていることが証明できます.検証者は以下の様にペアリングを用いて検証します.この検証には$G * k_a,G * 1$が必要なため,設定者はこれも公開する必要があります.$B(s),C(s)$についても同様です.
\displaylines{
e(G * A(s),G * k_a)\overset{?}{=}e(G * A(s) * k_a,G * 1)
}
次に,$A(s),B(s),C(s)$の作成に同じ割り当て$a_i$が使われていることを証明します.そのために,設定者は事前に以下の値を公開しておく必要があります.$k_d$はtoxic wasteであり,すぐに捨てる必要があります.
\displaylines{
G * (A_i(s)+B_i(s)+C_i(s)) * k_d
}
証明者は割り当て$a_i$を利用して証明$\pi_d$を作成します.
\displaylines{
\begin{align}
&a_1\left\{ G * (A_1(s) + B_1(s) + C_1(s)) * k_d \right\} \\
+&a_2\left\{ G * (A_2(s) + B_2(s) + C_2(s)) * k_d \right\} \\
&\vdots \\
+&a_n\left\{ G * (A_n(s) + B_n(s) + C_n(s)) * k_d \right\} \\
\\
=&G * (A(s)+B(s)+C(s)) * k_d \\
=&\pi_d
\end{align}
}
検証者は以下の様にペアリングを用いて検証し,同じ割り当て$a_i$が使われていることを確認します.
\displaylines{
e(G * (A(s)+B(s)+C(s)),G * k_d)\overset{?}{=}e(G * (A(s)+B(s)+C(s)) * k_d,G * 1)
}
重要なことを忘れていました.$h(s)$はどのように作成すればよいでしょうか.$h(x)$は証明者しか知らないため設定者は$h(s)$を作成できません.逆に,$s$は設定者しか知らないため証明者は$h(s)$を作ることが出来ません.しかし,$h(s)$がどのような形になるのかは既に分かっています.
\displaylines{
h(s)=\beta_0+\beta_1s+\beta_2s^2+\cdots+\beta_Ns^N
}
そこで,設定者は以下の値をTrusted Setupで公開することにします.
\displaylines{
G * s, \, G * s^2, \, \cdots, \, G * s^N
}
すると,証明者は以下の様に$h(s)$を計算出来るようになります.
\displaylines{
\begin{align}
&\beta_0(G * 1) +\beta_1(G * s) +\beta_2(G * s^2) + \beta_N(G * s^N) \\
=&G * (\beta_0+\beta_1s+\beta_2s^2+\cdots+\beta_Ns^N) \\
=&G * h(s)
\end{align}
}
最後に,$A(s)B(s)-C(s)=t(s)h(s)$かどうかを検証します.これは簡単で,検証者は以下のペアリングを検証します.なお,$G * t(s)$は設定者が公開する必要があります.
\frac{e(G * A(s),G * B(s))}{e(G * C(s),G * 1)}\overset{?}{=}e(G * t(s),G * h(s))
証明?を書いておくと,
\begin{align}
(左辺)&=\frac{e(G * 1,G * 1)^{A(s)B(s)}}{e(G * 1,G * 1)^{C(s)}} \\
&=e(G * 1,G * 1)^{A(s)B(s)-C(s)} \\
&=e(G * 1,G * 1)^{t(s)h(s)} \\
&=e(G * t(s),G * h(s)) \\
&=(右辺)
\end{align}
ここまでで,Trusted Setupの際に公開するパラメータと証明者が提出する証明に大幅な修正があったため一度まとめます.
- Trusted Setup 公開パラメータ
\displaylines{
G * A_i(s), \quad G * A_i(s) * k_a \\
G * B_i(s), \quad G * B_i(s) * k_b \\
G * C_i(s), \quad G * C_i(s) * k_c \\
}
\displaylines{
G * k_a, \ G * k_b, \ G * k_c, \ G * k_d, \ G * t(s)
}
\displaylines{
G * 1, \ G * s, \ G * s^2, \ \cdots, \ G * s^N
}
- toxic waste
\displaylines{
s, \ k_a, \ k_b, \ k_c, \ k_d
}
- 証明
\displaylines{
\pi_a=G * A(s), \quad \pi_a'=G * A(s) * k_a \\
\pi_b=G * B(s), \quad \pi_b'=G * B(s) * k_b \\
\pi_c=G * C(s), \quad \pi_c'=G * C(s) * k_c \\
}
\displaylines{
\pi_d=G * (A(s)+B(s)+C(s)) * k_d
}
\displaylines{
\pi_h=G * h(s)
}
Pinocchioプロトコルの流れ
必要なものが出揃ったので,Pinocchioプロトコルの流れを説明します.
- QAPの作成
証明者が証明したい問題とその解からQAPを作成します.
p(x)=\sum^n_{i=1}a_iA_i(x)\sum^n_{i=1}a_iB_i(x)-\sum^n_{i=1}a_iC_i(x) = t(x)h(x)
- Trusted Setup
設定者が検証に必要なパラメータを計算し,公開します.そして直ちにtoxic wasteを破棄します.- Trusted Setup 公開パラメータ
\displaylines{ G * A_i(s), \quad G * A_i(s) * k_a \\ G * B_i(s), \quad G * B_i(s) * k_b \\ G * C_i(s), \quad G * C_i(s) * k_c \\ }\displaylines{ G * k_a, \ G * k_b, \ G * k_c, \ G * k_d, \ G * t(s) }\displaylines{ G * 1, \ G * s, \ G * s^2, \ \cdots, \ G * s^N }- toxic waste
\displaylines{ s, \ k_a, \ k_b, \ k_c, \ k_d } - 証明の作成
証明者がパラメータを用いて証明を作成し,検証者に送信します.- 証明
\displaylines{ \pi_a=G * A(s), \quad \pi_a'=G * A(s) * k_a \\ \pi_b=G * B(s), \quad \pi_b'=G * B(s) * k_b \\ \pi_c=G * C(s), \quad \pi_c'=G * C(s) * k_c \\ }\displaylines{ \pi_d=G * (A(s)+B(s)+C(s)) * k_d }\displaylines{ \pi_h=G * h(s) } - 検証
検証者はペアリングを用いて証明を検証し,証明者の主張が正しいことを確認します.- $A(s),B(s),C(s)$が線形結合かどうかの検証
\displaylines{ e(\pi_a,G * k_a)\overset{?}{=}e(\pi_a',G) \\ e(\pi_b,G * k_b)\overset{?}{=}e(\pi_b',G) \\ e(\pi_c,G * k_c)\overset{?}{=}e(\pi_c',G) \\ }- $A(x),B(x),C(x)$が同じ割り当て(係数)かどうかの検証
e(\pi_a+\pi_b+\pi_c,G * k_d)\overset{?}{=}e(\pi_d,G)- $A(s)B(s)-C(s)=t(s)h(s)$かどうかの検証
\frac{e(\pi_a,\pi_b)}{e(\pi_c,G)}\overset{?}{=}e(G * t(s),\pi_h)
以上の流れでPinocchioプロトコルは完成です.
しかし,実際のPinocchioプロトコルはこの手順と異なる点が多々あります.興味のある方は元論文や参考記事をご覧ください.
まとめ
はじめに紹介したzkSNARKsの三つの要素が満たされていることが分かります.
- Zero-Knowledge: 検証者に送信する情報は全てECDLPにより秘匿されている
- Succinct: 膨大なゲート制約を一つの多項式で検証できる
- Non-interactive: Schwartz–Zippelの補題により証明を検証者に一回送るだけ
間違っている箇所多々あると思います.お知らせください.
補足
参考記事
