TL;DR
three.jsを使った立体図形の表示に関しては説明しているサイトが多くありましたが、その図形の展開方法についてはありませんでしたので一例としてまとめました。
HTML、JavaScript、three.jsについてある程度の知識を持っている方を対象としています。
three.jsを使って正四面体を展開するときのポイントは次の通りです。
- CylinderGeometry(三角柱)を4枚合わせる
- 各面の中心点(メッシュのposition)の「位置」を計算する
- 底面に対する各面の回転角を計算する
- 回転にQuaternionを用いる(回転軸を定義する)
- 計算には「ピタゴラスの定理」と「三角関数」を用いる
- 角度はラジアンで計算する
開発環境
- OS : Microsoft Windows 10 Home
- プロセッサ : Intel(R) Core(TM) i7-7500U CPU @ 2.70GHz、2904 Mhz、2 個のコア、4 個のロジカル プロセッサ
- メモリ : 16GB
- プログラミング言語 : JavaScript ※const、letは使用しますがIEを意識してアロー関数は使用していません
- ブラウザ: Google Chrome
説明の流れ
本記事では「three.jsで正四面体を展開する」という目的に必要な知識を次の順番に説明します。少々長い内容となりますが、ご容赦いただければと思います。
- 必要な数学知識
- 3D描画においては表示する座標を計算することが必要になります。小中高レベルの数学知識が役に立ちます。ここではその内容を説明します。
- ベースとなるHTMLコード
- JavaScriptの結果を画面に表示させるのに必要なHTMLについて説明します。
- 正四面体を表示するJavaScriptコード
- 展開をする前に表示方法を把握しているとコードに対する理解が深まりますので、先に説明します。
- 正四面体を展開するJavaScriptコード
- メインのコードです。クロージャを多用していますので読みづらい場合は、先にクロージャについて調べておくと読みやすくなるかもしれません。
1.必要な数学知識
1-1.円周の長さ
小学算数で一般に習う次の公式を用います。
「直径1の円の円周の長さを円周率という」

ですが円の問題を扱うときは直径ではなく、
その半分の「半径」を用いた方が分かりやすくなるため円周の定義としては次が広く知られています。
「半径1の円の円周の長さは円周率の2倍」
円周率は$\pi$(3.141592...)と表します。
JavaScriptではMath.PIで表します。
ラジアン表記の角度ではこの円周率が半円の角度(180°)を表します。
半円の角度はまっ平(水平)を表します。
その半分の$\pi$/2、JavaScriptではMath.PI/2が直角(90°)を表します。
1-2.三角形の内角の和
小学算数で一般に習う次の公式を用います。
「三角形の内角θ1、θ2、θ3の和は180°」

ラジアンで表すと次の通りです。
「三角形の内角θ1、θ2、θ3の和は$\pi$」
JavaScriptで表すと次の通りです。
Math.PI = θ1 + θ2 + θ3;
このあたりの知識を応用することで、直角三角形の直角以外の角度の和は90°ということが分かります。
例えばθ3が90°ならば、
Math.PI = θ1 + θ2 + Math.PI/2;
Math.PI/2 = θ1 + θ2;
1-3.平方根
中学数学で一般に習う次の定義を用います。
「2乗するとその値になる値のことを平方根という」
$$b = a^{2}$$
が成り立つとき、aをbの平方根といいます。
JavaScriptで表すと次の通りです。
b = Math.pow(a, 2);
に対して
a = Math.sqrt(b);
1-4.ピタゴラスの定理(三平方の定理)
中学数学で一般に習う次の公式を用います。
「辺a、b、cの "直角三角形" において、最も長い辺をcとした場合に次の式が成り立つ」
$$c^{2} = a^{2} + b^{2}$$

JavaScriptで表すと次の通りです。
Math.pow(c, 2) = Math.pow(a, 2) + Math.pow(b, 2);
1-5.三角関数
高校数学で一般に習う次の三角関数の定義を用います。
「辺a、b、cの "直角三角形" において、最も長い辺をc、垂直な辺をa、底辺をb、bとcの間の角度をθとした場合に次の式が成り立つ」
$$sinθ = a \div c$$
$$cosθ = b \div c$$
 ※矢印に沿って「分母」「分子」の順で考えると分かりやすいです。
※矢印に沿って「分母」「分子」の順で考えると分かりやすいです。
JavaScriptで表すと次の通りです。
Math.sin(θ) = a / c;
Math.cos(θ) = b / c;
sin、cosともに「割合」を表すと考えると分かりやすいです。
値の範囲は「-1~1」になります。
主な値は次の通りです。
| 角度 (度数) |
角度 (ラジアン) |
sin | cos |
|---|---|---|---|
| 0° | $0$ | $0$ | $1$ |
| 90° | $\pi\times1/2$ | $1$ | $0$ |
| 180° | $\pi$ | $0$ | $-1$ |
| 270° | $\pi\times3/2$ | $-1$ | $0$ |
| 360° | $\pi\times2$ | $0$ | $1$ |
この値を利用することで、「一つの辺の長さとそのどちらかの角度」が分かる直角三角形であれば、他の辺の長さを計算することができます。
斜辺に対して高さは「sin」をかけ、
底辺は「cos」をかけると求めることができます。

三角関数は他にもありますが、ここでは「sin」「cos」だけを知っていれば大丈夫です。
1-6.逆三角関数
高校数学で一般に習う逆三角関数の定義を用います。
「$sinθ = a \div c$が成り立つ場合、$θ = arcsin(a \div c)$と定義する」
「$cosθ = b \div c$が成り立つ場合、$θ = arccos(b \div c)$と定義する」
逆関数自体は非常に難しい概念ですが、ポイントは「2辺の角度を表す」ことです。
三角関数で扱ったsin、cosは「2辺の割合」であることに対して逆三角関数は「角度」です。
そのため角度の代わりに扱うことができます。
二辺の長さが決まっていてその角度がわからないときに用いるのがよいです。
JavaScriptで表すと次の通りです。
θ = Math.asin(a/c);
θ = Math.acos(b/c);

逆三角関数は他にもありますが、ここでは「asin」「acos」だけを知っていれば大丈夫です。
1-7.ベクトル
高校数学で一般に習うベクトルの概念を用います。
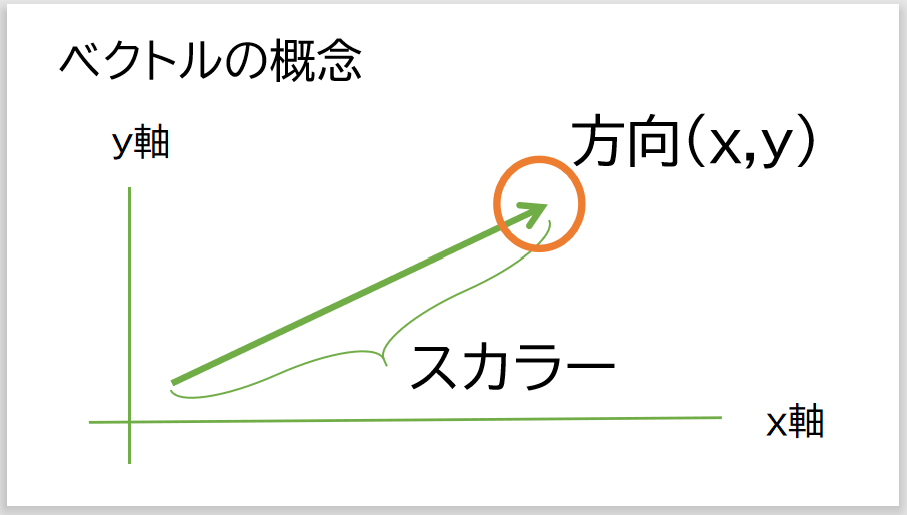
ベクトルはスカラーと呼ばれる「値」と「方向」を持つもので「矢印」をイメージすると分かりやすくなります。
矢印で表すと矢印の「長さ」がスカラーで矢印の「向き」が方向を表します。
向きは「座標」で表します。
2.ベースとなるHTMLコード
画面を定義するHTMLコードを説明します。
2-1.全体
コード全体を見る場合はここをクリックしてください
<!DOCTYPE html>
<html lang="ja">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>three.js 正四面体サンプル</title>
<script type="text/javascript" src="lib/three.min.js"></script>
<script type="text/javascript" src="lib/OrbitControls.js"></script>
<script type="text/javascript">
window.onload = function()
{
'use strict';
// TODO: ここに3D描画をするコードを書きます
};
</script>
</head>
<body>
<div class="rp4Wrap">
<h2>正四面体</h2>
<canvas id="rp4"></canvas>
</div>
<div class="rp4OpenWrap">
<h2>正四面体(展開)</h2>
<div style="margin-bottom:5px;">
<button id="btnOpen">展開</button>
<button id="btnReset">リセット</button>
</div>
<canvas id="rp4Open"></canvas>
</div>
</body>
</html>
2-2.個別説明
(1)必要ファイル
<script type="text/javascript" src="lib/three.min.js"></script>
<script type="text/javascript" src="lib/OrbitControls.js"></script>
実行には次のファイルが必要です。
three.min.js
three.jsのライブラリファイル。
公式サイトよりダウンロードできます。
OrbitControls.js
カメラコントロールライブラリ。
メインのライブラリには含まれていませんが、これを利用するとマウスでのカメラ制御が非常に簡単になります。
公式サイトからダウンロードしたファイルの次のパスにあります。
three.js-master/examples/js/controls
(2)実行トリガー
<script type="text/javascript">
window.onload = function()
{
'use strict';
// TODO: ここに3D描画をするコードを書きます
};
</script>
window.onloadイベントで読み込みが終わった後に3D描画処理を実行します。
念のためuse strictでstrictモードにし変数の宣言忘れなどに気づけるようにします。
(3)body部
<body>
<div class="rp4Wrap">
<h2>正四面体</h2>
<canvas id="rp4"></canvas>
</div>
<div class="rp4OpenWrap">
<h2>正四面体(展開)</h2>
<div style="margin-bottom:5px;">
<button id="btnOpen">展開</button>
<button id="btnReset">リセット</button>
</div>
<canvas id="rp4Open"></canvas>
</div>
</body>
正四面体の表示用と展開用の描画箇所を分けます。
描画はcanvasに行うためそれぞれにid属性を付けておきます。
展開の方は「展開」を実行するボタンと「リセット」をするボタンを用意しておきます。
識別できるようにこちらにもid属性を付けておきます。
3.正四面体を表示するJavaScriptコード
JavaScriptを使って正四面体を表示します。
Viewクラス内に2つのメソッドに分けて定義します。
- renderメソッド
- 画面に3D図形を描画する処理をまとめたメソッドです。
汎用的なコードのため使い回せる部分が多いものになります。
- 画面に3D図形を描画する処理をまとめたメソッドです。
- setSceneRP4メソッド
- 正四面体を表示する処理(シーンに設定する処理)のメソッドです。
正四面体が関わる処理がまとめられています。
- 正四面体を表示する処理(シーンに設定する処理)のメソッドです。
3-1.全体
window.onloadイベントの中に次のコードを入力します。
コード全体を見る場合はここをクリックしてください
/** defines */
const CANVAS_WIDTH = 960;
const CANVAS_HEIGHT = 540;
const CANVAS_TYPE_RP4 = 1;
/** classes */
const View = function() {};
View.prototype =
{
render: function(id, canvasType) {
const canvas = document.getElementById(id);
const renderer = new THREE.WebGLRenderer({
canvas: canvas,
antialias: true
});
renderer.setPixelRatio(window.devicePixelRatio);
renderer.setSize(CANVAS_WIDTH, CANVAS_HEIGHT);
const scene = new THREE.Scene();
scene.background = new THREE.Color(0xffffff);
const camera = new THREE.PerspectiveCamera(60, CANVAS_WIDTH / CANVAS_HEIGHT);
camera.position.set(2, 0, 9);
const controls = new THREE.OrbitControls(camera, canvas);
controls.enableDamping = true;
controls.dampingFactor = 0.2;
switch(canvasType) {
case CANVAS_TYPE_RP4:
this.setSceneRP4(scene);
break;
default:
// pass
}
/** 描画更新処理 */
const update = function() {
controls.update();
renderer.render(scene, camera);
requestAnimationFrame(update);
};
update();
},
setSceneRP4: function(scene) {
const createMesh = function() {
const geometry = new THREE.ConeGeometry(3, 3, 3);
const material = new THREE.MeshBasicMaterial({
color: 0xccffcc,
transparent: true,
opacity: 0.8
});
const mesh = new THREE.Mesh(geometry, material);
return mesh;
};
const createLine = function() {
const geometry = new THREE.ConeBufferGeometry(3, 3, 3);
const edges = new THREE.EdgesGeometry(geometry);
const material = new THREE.LineBasicMaterial({ color: 0x000000 });
const line = new THREE.LineSegments(edges, material);
return line;
};
scene.add(createMesh());
scene.add(createLine());
},
};
/** objects */
const view = new View();
/** run */
view.render('rp4', CANVAS_TYPE_RP4);
3-2.個別説明
(1)定義部
const CANVAS_WIDTH = 960;
const CANVAS_HEIGHT = 540;
const CANVAS_TYPE_RP4 = 1;
上部に利用する定数を定義します。
| 定数名 | 説明 |
|---|---|
| CANVAS_WIDTH | キャンバスの幅です |
| CANVAS_HEIGHT | キャンバスの高さです |
| CANVAS_TYPE_RP4 | 正四面体表示を表す定数です |
(2)renderメソッド
3D図形を指定されたキャンバスに描画します。
引数
| 引数名 | 説明 |
|---|---|
| id | 描画するcanvasのid |
| canvasType | 定数定義された「CANVAS_TYPE_~」の値 |
戻り値
なし
各コード説明
const canvas = document.getElementById(id);
引数で渡されたcanvasのHTMLエレメントを取得します。
const renderer = new THREE.WebGLRenderer({
canvas: canvas,
antialias: true
});
renderer.setPixelRatio(window.devicePixelRatio);
renderer.setSize(CANVAS_WIDTH, CANVAS_HEIGHT);
画面描画をするクラスのインスタンスを生成します。
描画先のキャンバスのHTMLエレメントと、アンチエイリアスを利用する設定を渡します。
アンチエイリアスを有効にすることで滑らかな表示にしています。
画面調整は「setPixelRatio」「setSize」で行うと考えおくのがよいです。
const scene = new THREE.Scene();
scene.background = new THREE.Color(0xffffff);
シーンのインスタンスを生成します。
ここでは背景を白(0xffffff)で設定します。
const camera = new THREE.PerspectiveCamera(60, CANVAS_WIDTH / CANVAS_HEIGHT);
camera.position.set(2, 0, 9);
カメラのインスタンスを生成します。
ここではパースペクティブカメラ(遠近感のあるカメラ)を用います。
視野角は60°に設定しています。
初期座標は少し右からみて、すこし引くイメージで、
x=2、z=9と指定します。
three.jsでは、各座標とプラスマイナスの関係は次のようになります。
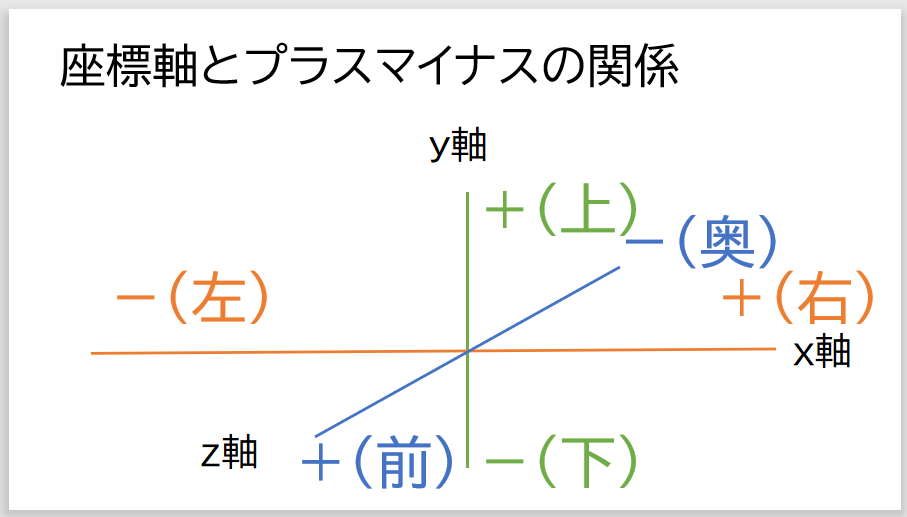
ここでは使用していませんが、「THREE.AxesHelper」を利用するとプラスの方向の座標軸が表示されるようになります。
マイナスの方向には表示されません。
const controls = new THREE.OrbitControls(camera, canvas);
controls.enableDamping = true;
controls.dampingFactor = 0.2;
カメラ制御のインスタンスを生成します。
操作が滑らかになるようにプロパティを設定します。
switch(canvasType) {
case CANVAS_TYPE_RP4:
this.setSceneRP4(scene);
break;
default:
// pass
}
引数で渡されたタイプ情報を元に後述の描画関数「setSceneRP4」を呼び出します。
const update = function() {
controls.update();
renderer.render(scene, camera);
requestAnimationFrame(update);
};
update();
再帰的に呼ばれるアニメーション処理を定義します。
ここではカメラの制御更新と描画オブジェクトの位置や回転が
指定された場合の表示更新をしています。
「requestAnimationFrame」に自身の関数を渡すことで連続実行をしています。
(3)setSceneRP4メソッド
正四面体を引数で渡されたシーンに追加します。
引数
| 引数名 | 説明 |
|---|---|
| scene | シーンオブジェクト |
戻り値
なし
各コード説明
const createMesh = function() {
const geometry = new THREE.ConeGeometry(3, 3, 3);
const material = new THREE.MeshBasicMaterial({
color: 0xccffcc,
transparent: true,
opacity: 0.8
});
const mesh = new THREE.Mesh(geometry, material);
return mesh;
};
正四面体のメッシュを生成する処理です。
ジオメトリには「ConeGeometry」を用います。
ここでは1辺が3の長さの正三角形の四面体に指定しています。
マテリアルはopacityで半透明に指定しています。
const createLine = function() {
const geometry = new THREE.ConeBufferGeometry(3, 3, 3);
const edges = new THREE.EdgesGeometry(geometry);
const material = new THREE.LineBasicMaterial({ color: 0x000000 });
const line = new THREE.LineSegments(edges, material);
return line;
};
ラインのメッシュを生成する処理です。
作成する正四面体は各辺に線を引きます。
単に「ConeGeometry」で生成するだけでは線はできないため、
別に「ConeGeometry」の縁に線を引いたメッシュを用意して、「同一座標」に表示させています。
似たような方法で「ConeGeometry」でwireframeのプロパティを設定することもできますが、
この場合は不要な対角線なども表示されてしまうため、「EdgesGeometry」を利用して縁のみを表示するようにしています。
scene.add(createMesh());
scene.add(createLine());
正四面体のメッシュと線のみのメッシュをシーンに追加します。
(4)呼び出し処理
const view = new View();
作成したクラスのインスタンスを生成します。
view.render('rp4', CANVAS_TYPE_RP4);
表示先のキャンバスのidを指定して正四面体の描画処理を呼び出します。
(5)動作確認
ここまでのコードを書いたらブラウザで開いて次の確認をします。
- 正四面体が正しく表示されること
4.正四面体を展開するJavaScriptコード
JavaScriptを使って正四面体を展開します。
Viewクラス内にsetSceneRP4Openメソッドを追加して、renderメソッドを更新します。
- renderメソッド(更新あり)
- 画面に3D図形を描画する処理をまとめたメソッドです。
汎用的なコードのため使い回せる部分が多いものになります。
- 画面に3D図形を描画する処理をまとめたメソッドです。
- setSceneRP4Openメソッド
- 正四面体を展開する処理(シーンに設定する処理)のメソッドです。
内部的に「表示の設定をする」部分と「展開の設定をする」部分に分かれています。
- 正四面体を展開する処理(シーンに設定する処理)のメソッドです。
4-1.全体
※「追加 START」~「追加 END」までが追加行になります。
コード全体を見る場合はここをクリックしてください(先ほどのコード全体より長めです)
/** defines */
const CANVAS_WIDTH = 960;
const CANVAS_HEIGHT = 540;
const CANVAS_TYPE_RP4 = 1;
// 追加 START-----------------------------------
const CANVAS_TYPE_RP4_OPEN = 2;
const ANIM_STATUS_STAY = 0;
const ANIM_STATUS_WAIT_START = 1;
const ANIM_STATUS_EXECUTING = 2;
const ANIM_STATUS_DONE = 3;
const ANIM_STATUS_WAIT_RESET = 4;
// 追加 END-------------------------------------
/** classes */
const View = function() {
// 追加 START-----------------------------------
this.animationStatus = {
renderCanvas4Open: ANIM_STATUS_STAY
};
// 追加 END-------------------------------------
};
View.prototype =
{
render: function(id, canvasType) {
const canvas = document.getElementById(id);
const renderer = new THREE.WebGLRenderer({
canvas: canvas,
antialias: true
});
renderer.setPixelRatio(window.devicePixelRatio);
renderer.setSize(CANVAS_WIDTH, CANVAS_HEIGHT);
const scene = new THREE.Scene();
scene.background = new THREE.Color(0xffffff);
const camera = new THREE.PerspectiveCamera(60, CANVAS_WIDTH / CANVAS_HEIGHT);
camera.position.set(2, 0, 9);
const controls = new THREE.OrbitControls(camera, canvas);
controls.enableDamping = true;
controls.dampingFactor = 0.2;
// 追加 START-----------------------------------
let interval;
// 追加 END-------------------------------------
switch(canvasType) {
case CANVAS_TYPE_RP4:
this.setSceneRP4(scene);
break;
// 追加 START-----------------------------------
case CANVAS_TYPE_RP4_OPEN:
interval = this.setSceneRP4Open(scene);
break;
// 追加 END-------------------------------------
default:
// pass
}
/** 描画更新処理 */
const update = function() {
// 追加 START-----------------------------------
if (typeof interval !== 'undefined') {
interval();
}
// 追加 END-------------------------------------
controls.update();
renderer.render(scene, camera);
requestAnimationFrame(update);
};
update();
},
setSceneRP4: function(scene) {
const createMesh = function() {
const geometry = new THREE.ConeGeometry(3, 3, 3);
const material = new THREE.MeshBasicMaterial({
color: 0xccffcc,
transparent: true,
opacity: 0.8
});
const mesh = new THREE.Mesh(geometry, material);
return mesh;
};
const createLine = function() {
const geometry = new THREE.ConeBufferGeometry(3, 3, 3);
const edges = new THREE.EdgesGeometry(geometry);
const material = new THREE.LineBasicMaterial({ color: 0x000000 });
const line = new THREE.LineSegments(edges, material);
return line;
};
scene.add(createMesh());
scene.add(createLine());
},
// 追加 START(上のコンマから)-----------------------------------
setSceneRP4Open: function(scene) {
const that = this;
// 辺の長さ
const length = 3;
// 上部3面の傾き角度(ラジアン)
const angle = Math.acos(1/3);
// 原点からx軸に平行な辺に下した垂線の長さ
const oa = length / 2;
// 原点と移動先中心点を結んだ線分の角度
const rad = (Math.PI - angle) / 2;
// 原点から移動先までの距離
const ab = oa * Math.sin(angle/2) * 2;
// 原点から移動先までの高さ
const h = ab * Math.sin(rad);
// 原点から移動先までの幅
const w = ab * Math.cos(rad);
/** 位置を設定する */
const setPosition = function(index, mesh) {
mesh.position.y = -1 * length / 2;
// 回転させるためのクォータニオンを取得
const quaternion = mesh.quaternion;
const target = new THREE.Quaternion();
let axis = null;
switch (index) {
case 0:
// 回転
axis = new THREE.Vector3(-1, 0, 0).normalize();
target.setFromAxisAngle(axis, angle);
quaternion.multiply(target);
// 移動
mesh.position.x = 0;
mesh.position.y += h;
mesh.position.z += -1 * w;
break;
case 1:
// 回転
axis = new THREE.Vector3(1, 0, -1 * Math.sqrt(3)).normalize();
target.setFromAxisAngle(axis, angle);
quaternion.multiply(target);
// 移動
mesh.position.x += w * Math.cos(Math.PI/6);
mesh.position.y += h;
mesh.position.z += w * Math.sin(Math.PI/6);
break;
case 2:
// 回転
axis = new THREE.Vector3(1, 0, Math.sqrt(3)).normalize();
target.setFromAxisAngle(axis, angle);
quaternion.multiply(target);
// 移動
mesh.position.x += -1 * w * Math.cos(Math.PI/6);
mesh.position.y += h;
mesh.position.z += w * Math.sin(Math.PI/6);
break;
case 3:
// 底面のため何もしない
break;
default:
// pass
}
};
/** メッシュを生成する */
const createMesh = function(index) {
const geometry = new THREE.CylinderGeometry(length, length, 0.01, 3, 1);
const material = new THREE.MeshBasicMaterial({
color: 0xccffcc,
transparent: true,
opacity: 0.8
});
const mesh = new THREE.Mesh(geometry, material);
setPosition(index, mesh);
return mesh;
};
/** 線を生成する */
const createLine = function(index) {
const geometry = new THREE.CylinderBufferGeometry(length, length, 0.01, 3, 1);
const edges = new THREE.EdgesGeometry(geometry);
const material = new THREE.LineBasicMaterial({ color: 0x000000 });
const line = new THREE.LineSegments(edges, material);
setPosition(index, line);
return line;
};
for (var i = 0; i < 4; i++) {
scene.add(createMesh(i));
scene.add(createLine(i));
}
// 100回で展開完了になるように移動・回転する
const moveAngle = (Math.PI - angle) / 100;
that.count = 0;
that.angle = angle;
// リセット用に位置と回転情報を保存
let orgChildren = [];
for (let i = 0; i < scene.children.length; i++) {
let child = {};
child.position = {};
child.rotation = {};
child.position.x = scene.children[i].position.x;
child.position.y = scene.children[i].position.y;
child.position.z = scene.children[i].position.z;
child.rotation.x = scene.children[i].rotation.x;
child.rotation.y = scene.children[i].rotation.y;
child.rotation.z = scene.children[i].rotation.z;
orgChildren.push(child);
}
/** 展開処理 */
const open = function() {
const status = that.animationStatus['renderCanvas4Open'];
if (status === ANIM_STATUS_STAY) {
return;
}
else if (status === ANIM_STATUS_WAIT_START) {
that.animationStatus['renderCanvas4Open'] = ANIM_STATUS_EXECUTING;
}
else if (status === ANIM_STATUS_EXECUTING) {
// pass
}
else if (status === ANIM_STATUS_WAIT_RESET) {
for (let i = 0; i < scene.children.length; i++) {
scene.children[i].position.x = orgChildren[i].position.x;
scene.children[i].position.y = orgChildren[i].position.y;
scene.children[i].position.z = orgChildren[i].position.z;
scene.children[i].rotation.x = orgChildren[i].rotation.x;
scene.children[i].rotation.y = orgChildren[i].rotation.y;
scene.children[i].rotation.z = orgChildren[i].rotation.z;
}
that.animationStatus['renderCanvas4Open'] = ANIM_STATUS_STAY;
that.count = 0;
that.angle = angle;
return;
}
// else if (status === ANIM_STATUS_EXECUTING) { }
// else if (status === ANIM_STATUS_DONE) { }
else {
return;
}
// angleがMath.PIになると展開完了のため処理を抜ける
if (that.angle >= Math.PI) {
that.animationStatus['renderCanvas4Open'] = ANIM_STATUS_DONE;
return;
}
that.count++;
let nextAngle = that.angle + moveAngle;
if (nextAngle > Math.PI) {
nextAngle = Math.PI;
}
const w = length/2 * (Math.cos(that.angle) - Math.cos(nextAngle));
const h = length/2 * (Math.sin(nextAngle) - Math.sin(that.angle));
that.angle = nextAngle;
/** 各図形の展開処理(indexはsceneの子要素インデックス) */
const openMesh = function(index) {
const quaternion = scene.children[index].quaternion;
const target = new THREE.Quaternion();
let axis = new THREE.Vector3(0, 0, 0);
switch (index) {
case 0:
case 1:
// 回転
axis = new THREE.Vector3(-1, 0, 0).normalize();
target.setFromAxisAngle(axis, moveAngle);
quaternion.multiply(target);
// 移動
scene.children[index].position.y += h;
scene.children[index].position.z -= w;
break;
case 2:
case 3:
// 回転
axis = new THREE.Vector3(1, 0, -1 * Math.sqrt(3)).normalize();
target.setFromAxisAngle(axis, moveAngle);
quaternion.multiply(target);
// 移動
scene.children[index].position.x += w * Math.cos(Math.PI/6);
scene.children[index].position.y += h;
scene.children[index].position.z += w * Math.sin(Math.PI/6);
break;
case 4:
case 5:
// 回転
axis = new THREE.Vector3(1, 0, Math.sqrt(3)).normalize();
target.setFromAxisAngle(axis, moveAngle);
quaternion.multiply(target);
// 移動
scene.children[index].position.x += -1 * w * Math.cos(Math.PI/6);
scene.children[index].position.y += h;
scene.children[index].position.z += w * Math.sin(Math.PI/6);
break;
default:
// pass
}
}
for (let i = 0; i < 6; i++) {
openMesh(i);
}
};
return open;
}
// 追加 END-------------------------------------
};
/** objects */
const view = new View();
// 追加 START-----------------------------------
/** events */
document.getElementById('btnOpen').addEventListener('click', function() {
view.animationStatus['renderCanvas4Open'] = ANIM_STATUS_WAIT_START;
});
document.getElementById('btnReset').addEventListener('click', function() {
view.animationStatus['renderCanvas4Open'] = ANIM_STATUS_WAIT_RESET;
});
// 追加 END-------------------------------------
/** run */
view.render('rp4', CANVAS_TYPE_RP4);
// 追加 START-----------------------------------
view.render('rp4Open', CANVAS_TYPE_RP4_OPEN);
// 追加 END-------------------------------------
4-2.個別説明
(1)定義部(更新)
const CANVAS_TYPE_RP4_OPEN = 2;
const ANIM_STATUS_STAY = 0;
const ANIM_STATUS_WAIT_START = 1;
const ANIM_STATUS_EXECUTING = 2;
const ANIM_STATUS_DONE = 3;
const ANIM_STATUS_WAIT_RESET = 4;
上部に利用する定数を追加定義します。
| 定数名 | 説明 |
|---|---|
| CANVAS_TYPE_RP4_OPEN | 正四面体展開を表す定数です |
| ANIM_STATUS_STAY | 「待機中」を表すアニメーションのステータスです |
| ANIM_STATUS_WAIT_START | 「展開待ち」を表すアニメーションのステータスです |
| ANIM_STATUS_EXECUTING | 「展開中」を表すアニメーションのステータスです |
| ANIM_STATUS_DONE | 「展開終了」を表すアニメーションのステータスです |
| ANIM_STATUS_WAIT_RESET | 「リセット待ち」を表すアニメーションのステータスです |
「ANIM_STATUS_~」はボタン操作に関する状態を表す定数です。
const View = function() {
// 追加 START-----------------------------------
this.animationStatus = {
renderCanvas4Open: ANIM_STATUS_STAY
};
// 追加 END-------------------------------------
};
クラスのコンストラクタに状態初期化の処理を追加します。
「renderCanvas4Open」というキーが正四面体展開を表します。
(2)renderメソッド(更新)
定義に変更はありません。
各コード説明
// 追加 START-----------------------------------
let interval;
// 追加 END-------------------------------------
switch(canvasType) {
case CANVAS_TYPE_RP4:
this.setSceneRP4(scene);
break;
// 追加 START-----------------------------------
case CANVAS_TYPE_RP4_OPEN:
interval = this.setSceneRP4Open(scene);
break;
// 追加 END-------------------------------------
default:
// pass
}
後述の「setSceneRP4Open」メソッドは連続処理の関数を返します。
その返却値を受け取れるように「interval」変数を定義します。
正四面体展開する「setSceneRP4Open」メソッドの呼び出し処理を追加します。
const update = function() {
// 追加 START-----------------------------------
if (typeof interval !== 'undefined') {
interval();
}
// 追加 END-------------------------------------
controls.update();
renderer.render(scene, camera);
requestAnimationFrame(update);
};
interval変数が定義されている場合には、その変数を実行する処理を追加します。
intervalは変数でも関数を表すため、関数形式の「interval()」と書きます。
(3)setSceneRP4Openメソッド
正四面体を引数で渡されたシーンに追加します。
また展開処理の関数を返します。
引数
| 引数名 | 説明 |
|---|---|
| scene | シーンオブジェクト |
戻り値
展開処理の関数
各コード説明
const that = this;
クロージャ内でこのメソッド自身を呼び出したいため、that変数に自分自身を格納しておきます。
// 辺の長さ
const length = 3;
正四面体の辺の長さです。
// 上部3面の傾き角度(ラジアン)
const angle = Math.acos(1/3);
今回は「setSceneRP4」メソッドとは異なり、正四面体を4つの三角形を結合して作成します。
そのときに必要になる上部3面の底面に対する角度です。
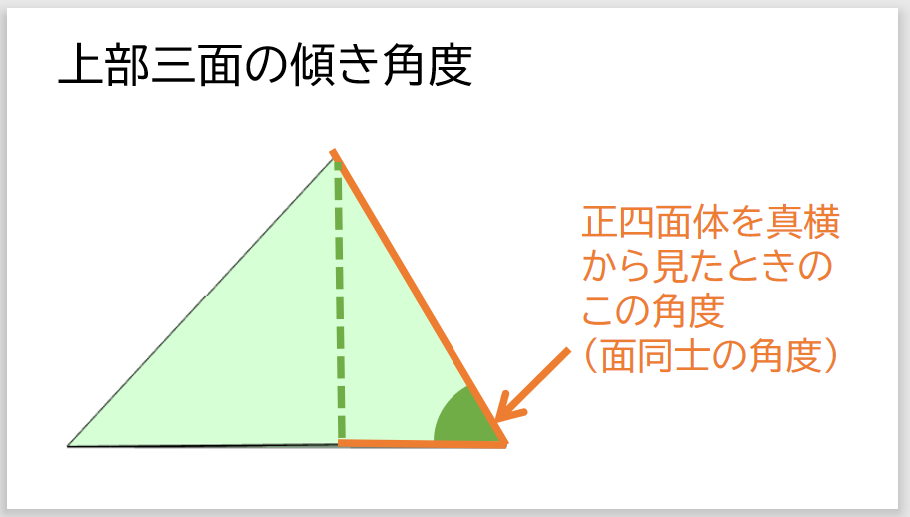
正四面体の最上部の頂点から底面に対して垂線を下ろした場合、
底面の中心に対して1/3の部分と交わるため、逆関数を使って角度を計算しています。
※証明は割愛しま。す

// 原点からx軸に平行な辺に下した垂線の長さ
const oa = length / 2;
// 原点と移動先中心点を結んだ線分の角度
const rad = (Math.PI - angle) / 2;
// 原点から移動先までの距離
const ab = oa * Math.sin(angle/2) * 2;
// 原点から移動先までの高さ(2次元におけるyに相当)
const h = ab * Math.sin(rad);
// 原点から移動先までの幅(2次元におけるxに相当)
const w = ab * Math.cos(rad);
ここではsetPositionで利用する、座標計算に必要な値を計算します。
考え方としては、底面の位置に4枚の正三角形を配置し、
1枚ずつ立てて辺と頂点を合わせていくイメージです。
この立てる行為を「回転」、頂点と合わせていく行為を「移動」と考えます。
つまりは「回転」させた後に「移動」をさせるイメージを持つとわかりやすいです。

o、a、bはそれぞれ三角形の頂点を表し、頂点同士をつないだ辺をoa、ob、abとします。
わかりやすくするためx軸を抜きで考えます。
そのためにx軸のプラス側からzy座標の平面(2次元)を見ていると考えます。
oを原点(底面の中心点)とします。
aを回転後(立てた後)の下にある辺の中心点とします。
bを底面のうちx軸と平行になっている辺の中心点とします。

oaの長さですが、これはthree.jsがどこに表示しているかを把握する必要があるため、
頂点の情報を出力して確認します。
底面の頂点の情報を出力すると次のようになります。
0: n {x: 0, y: 0.004999999888241291, z: 3}
1: n {x: 2.598076105117798, y: 0.004999999888241291, z: -1.5}
2: n {x: -2.598076105117798, y: 0.004999999888241291, z: -1.5}
3: n {x: 0, y: -0.004999999888241291, z: 3}
4: n {x: 2.598076105117798, y: -0.004999999888241291, z: -1.5}
5: n {x: -2.598076105117798, y: -0.004999999888241291, z: -1.5}
6: n {x: 0, y: 0.004999999888241291, z: 0}
7: n {x: 0, y: -0.004999999888241291, z: 0}
次のようなコードで上記の出力がされ頂点を確認することができます。
ジオメトリの「vertices」プロパティを出力します。
// 参考: 頂点情報を出力する
console.log(index, mesh.geometry.vertices);
このz座標でマイナスになっている値が底面のx軸と平行な辺のz座標になります。
この値は三角形の1辺の半分になります。そのためoaは次の式で表せます。
// 原点からx軸に平行な辺に下した垂線の長さ
const oa = length / 2;
またbは回転させる前の座標のため、obはoaと等しくなります。

今度は移動後の中心点とz軸との角度を求めます。
aからz軸に平行な線と、移動後の中心点とbの延長線が交わるところで菱形ができます。
つまり4辺が同じ長さになります。
aの座標の部分で考えると、移動後の中心点とz軸の角度は、180°から
面の傾き角度を半分にした値ということがわかります。
// 原点と移動先中心点を結んだ線分の角度
const rad = (Math.PI - angle) / 2;
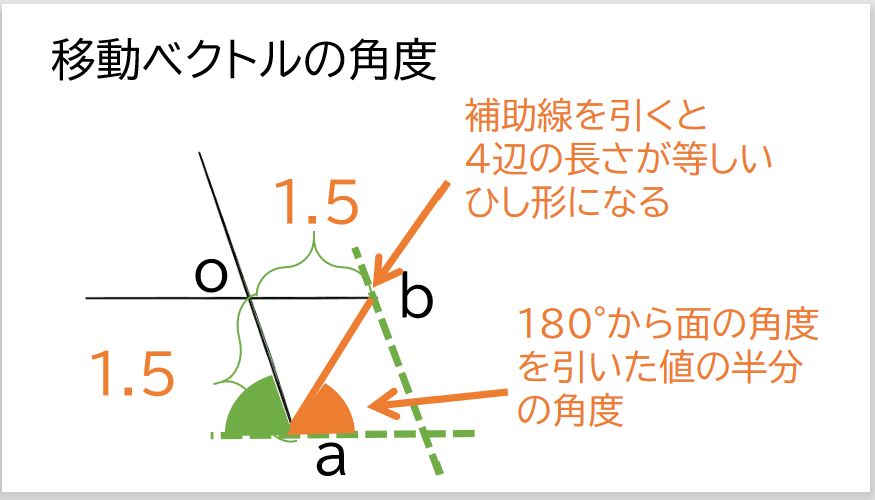
原点から移動後の中心点までの距離はabの長さと等しくなるためabの長さを求めます。
oabの二等辺三角形に対して、まずはoから垂線を下ろし直角三角形で考えます。
oの部分の角度は面の傾き角度の半分になるためabの半分の長さは
$$oa \times sin(面の傾き/2)$$
になります。abは上記の2倍のため次のようになります。
// 原点から移動先までの距離
const ab = oa * Math.sin(angle/2) * 2;
原点から移動後の中心点とその点を結んだ線分とz軸の角度がわかりましたので、
移動後の座標は次の通りになります。
$$y座標: ab \times sin(θ)$$
$$z座標: ab \times cos(θ)$$
JavaScriptで表すと次のようになります。
// 原点から移動先までの高さ
const h = ab * Math.sin(rad);
// 原点から移動先までの幅
const w = ab * Math.cos(rad);
ここで注意が必要なのは今計算している面については、
移動後の中心点のz座標は原点より奥にありますので、
wについては-1をかけてマイナスにした値が座標になります。
ここでは他の面でもこの計算結果を使うため、マイナスをかけるのは
実際に位置を指定するタイミングにしています。
(4)setPositionクロージャ
各面ごとの位置および回転を設定します。
引数
| 引数名 | 説明 |
|---|---|
| index | 各面につけられたインデックス(0~3) |
| mesh | 位置や角度を設定する対象の面 |
戻り値
なし
mesh.position.y = -1 * length / 2;
先に表示した正四面体と同じ位置に表示させるためy座標における位置を少し下げます。
// 回転させるためのクォータニオンを取得
const quaternion = mesh.quaternion;
const target = new THREE.Quaternion();
回転を設定するための準備です。定型コードと考えて大丈夫です。
case 0:
// 回転
axis = new THREE.Vector3(-1, 0, 0).normalize();
target.setFromAxisAngle(axis, angle);
quaternion.multiply(target);
// 移動
mesh.position.x = 0;
mesh.position.y += h;
mesh.position.z += -1 * w;
break;
case0はx軸と平行な底辺を持つ面を指します。
axis = new THREE.Vector3(-1, 0, 0).normalize();
target.setFromAxisAngle(axis, angle);
quaternion.multiply(target);
回転のコードですが、Quaternionは回転軸(ベクトル)を中心に回転をするのでその軸を決めます。
x軸のプラスの方向の軸とした場合に回転をさせるとその軸よりz座標が
正の位置にある頂点は反時計回り(yが減算される)に回転されます。
これは「ねじを抜くとき」をイメージするとわかりやすいです。
ねじを抜くときは同じく反時計回りに回します。
今回はこの回転の逆にしたいため、x座標がマイナスのベクトルを指定します。
「setFromAxisAngle」により回転の設定をしますが、
このときに渡すベクトルが正規化されていないと、拡大・縮小されてしまうため、
「normalize」をして回転のみされるようにします。
「multiply」を実行することで回転します。
描画の更新をしていないため、実際はまだ回転はしません。
mesh.position.x = 0;
mesh.position.y += h;
mesh.position.z += -1 * w;
移動後の面の中心点の位置を指定します。
x座標については移動しないので0のままです。
y座標については計算した「原点から移動先までの高さ」を追加して移動させます。
z座標については計算した「原点から移動先までの幅」を追加しますが、
z座標では奥がマイナスになるため、-1をかけた値を追加します。
case 1:
// 回転
axis = new THREE.Vector3(1, 0, -1 * Math.sqrt(3)).normalize();
target.setFromAxisAngle(axis, angle);
quaternion.multiply(target);
// 移動
mesh.position.x += w * Math.cos(Math.PI/6);
mesh.position.y += h;
mesh.position.z += w * Math.sin(Math.PI/6);
break;
case1はx座標がプラス側の面を指します。
axis = new THREE.Vector3(1, 0, -1 * Math.sqrt(3)).normalize();
target.setFromAxisAngle(axis, angle);
quaternion.multiply(target);
今回の回転軸は底面の辺に沿ってx座標がプラス、z座標がマイナスの方になります。
直角三角形で座標を考え、x座標を1とすると、次の計算式よりz座標は$-\sqrt{3}$になります。
一番長い辺の長さをcとすると、次の通り計算できます。
$$sin30° = 1 \div c$$
$$c = 1 \div sin30°$$
$$c = 2$$
三平方の定理より、残りの一辺b、つまりはz座標も求めることができます。
$$c^{2} = b^{2} + 1^{2}$$
$$4 = b^{2} + 1$$
$$b^{2} = 3$$
$$b = \sqrt{3}$$
今回はz座標は奥を指すため、-1をかけます。
mesh.position.x += w * Math.cos(Math.PI/6);
mesh.position.y += h;
mesh.position.z += w * Math.sin(Math.PI/6);
移動後の面の中心点の位置を指定します。
x座標については計算した「原点から移動先までの幅」を斜線とした直角三角形の辺を求める方法で、x座標を加算します。
y座標については計算した「原点から移動先までの高さ」を追加して移動させます。
z座標については計算した「原点から移動先までの幅」を斜線とした直角三角形の辺を求める方法で、x座標を加算します。
case 2:
// 回転
axis = new THREE.Vector3(1, 0, Math.sqrt(3)).normalize();
target.setFromAxisAngle(axis, angle);
quaternion.multiply(target);
// 移動
mesh.position.x += -1 * w * Math.cos(Math.PI/6);
mesh.position.y += h;
mesh.position.z += w * Math.sin(Math.PI/6);
break;
case2はx座標がマイナス側の面を指します。
axis = new THREE.Vector3(1, 0, Math.sqrt(3)).normalize();
target.setFromAxisAngle(axis, angle);
quaternion.multiply(target);
今回の回転軸は底面の辺に沿ってx座標がマイナス、z座標がマイナスの方になります。
直角三角形で座標を考えるとcase1同様にz座標は$-\sqrt{3}$になります。
mesh.position.x += -1 * w * Math.cos(Math.PI/6);
mesh.position.y += h;
mesh.position.z += w * Math.sin(Math.PI/6);
移動に関してはcase1に対してx座標がマイナスになります。
const createMesh = function(index) {
const geometry = new THREE.CylinderGeometry(length, length, 0.01, 3, 1);
const material = new THREE.MeshBasicMaterial({
color: 0xccffcc,
transparent: true,
opacity: 0.8
});
const mesh = new THREE.Mesh(geometry, material);
setPosition(index, mesh);
return mesh;
};
正四面体のメッシュを生成する処理です。
ジオメトリには「CylinderGeometry」を用います。
この三角柱の高さを非常に小さい値にして平面同様にしています。
平面のジオメトリを使ってしまうと3次元では見えない角度があるので
「CylinderGeometry」を利用しています。
マテリアルのオプションは先の正四面体と同様です。
メッシュ生成後に「setPosition」を呼び出して「回転」と「移動」をしています。
const createLine = function(index) {
const geometry = new THREE.CylinderBufferGeometry(length, length, 0.01, 3, 1);
const edges = new THREE.EdgesGeometry(geometry);
const material = new THREE.LineBasicMaterial({ color: 0x000000 });
const line = new THREE.LineSegments(edges, material);
setPosition(index, line);
return line;
};
ラインのメッシュを生成する処理です。
先の正四面体同様に作成する三角形の各辺に線を引きます。
面と同じ座標になるため、ここでも「setPosition」で「回転」と「移動」をします。
for (var i = 0; i < 4; i++) {
scene.add(createMesh(i));
scene.add(createLine(i));
}
正四面体の各面のメッシュと線のみのメッシュをシーンに追加します。
// 100回で展開完了になるように移動・回転する
const moveAngle = (Math.PI - angle) / 100;
that.count = 0;
that.angle = angle;
// リセット用に位置と回転情報を保存
let orgChildren = [];
for (let i = 0; i < scene.children.length; i++) {
let child = {};
child.position = {};
child.rotation = {};
child.position.x = scene.children[i].position.x;
child.position.y = scene.children[i].position.y;
child.position.z = scene.children[i].position.z;
child.rotation.x = scene.children[i].rotation.x;
child.rotation.y = scene.children[i].rotation.y;
child.rotation.z = scene.children[i].rotation.z;
orgChildren.push(child);
}
展開の前処理です。
今回は100回の展開処理実行完了となるように、展開範囲の角度を100で割ります。
リセット用に展開前の位置と回転の情報を保存します。
「position」「rotation」ともに読み取り専用のプロパティのため、
各値を取り出して格納しています。
const status = that.animationStatus['renderCanvas4Open'];
if (status === ANIM_STATUS_STAY) {
return;
}
else if (status === ANIM_STATUS_WAIT_START) {
that.animationStatus['renderCanvas4Open'] = ANIM_STATUS_EXECUTING;
}
else if (status === ANIM_STATUS_EXECUTING) {
// pass
}
else if (status === ANIM_STATUS_WAIT_RESET) {
for (let i = 0; i < scene.children.length; i++) {
scene.children[i].position.x = orgChildren[i].position.x;
scene.children[i].position.y = orgChildren[i].position.y;
scene.children[i].position.z = orgChildren[i].position.z;
scene.children[i].rotation.x = orgChildren[i].rotation.x;
scene.children[i].rotation.y = orgChildren[i].rotation.y;
scene.children[i].rotation.z = orgChildren[i].rotation.z;
}
that.animationStatus['renderCanvas4Open'] = ANIM_STATUS_STAY;
that.count = 0;
that.angle = angle;
return;
}
// else if (status === ANIM_STATUS_EXECUTING) { }
// else if (status === ANIM_STATUS_DONE) { }
else {
return;
}
設定されたステータスに応じて処理を分けています。
// angleがMath.PIになると展開完了のため処理を抜ける
if (that.angle >= Math.PI) {
that.animationStatus['renderCanvas4Open'] = ANIM_STATUS_DONE;
return;
}
平面になった場合はステータスを完了にします。
that.count++;
let nextAngle = that.angle + moveAngle;
if (nextAngle > Math.PI) {
nextAngle = Math.PI;
}
次の角度として移動角度を加算した値を設定します。
const w = length/2 * (Math.cos(that.angle) - Math.cos(nextAngle));
const h = length/2 * (Math.sin(nextAngle) - Math.sin(that.angle));
that.angle = nextAngle;
移動距離を計算しています。
幅は斜線(length/2)に現在の角度と移動後の角度の差をかけて求めます。
case 0:
case 1:
// 回転
axis = new THREE.Vector3(-1, 0, 0).normalize();
target.setFromAxisAngle(axis, moveAngle);
quaternion.multiply(target);
// 移動
scene.children[index].position.y += h;
scene.children[index].position.z -= w;
break;
回転は正四面体を表示させた時と同様です。
移動はy座標には移動高さ分を追加します。
x座標は動きませんので何も指定していません。
z座標には移動幅分を引きます。(奥に移動するため)
case 2:
case 3:
// 回転
axis = new THREE.Vector3(1, 0, -1 * Math.sqrt(3)).normalize();
target.setFromAxisAngle(axis, moveAngle);
quaternion.multiply(target);
// 移動
scene.children[index].position.x += w * Math.cos(Math.PI/6);
scene.children[index].position.y += h;
scene.children[index].position.z += w * Math.sin(Math.PI/6);
break;
こちらも回転は正四面体を表示させた時と同様です。
移動はy座標には移動高さ分を追加するのは先ほどと同じです。
x座標は移動幅分に正三角形の内角の半分(30°=$\pi/6$)のcosをかけたものを足します。
z座標は移動幅分に正三角形の内角の半分(30°=$\pi/6$)のsinをかけたものを足します。
case 4:
case 5:
// 回転
axis = new THREE.Vector3(1, 0, Math.sqrt(3)).normalize();
target.setFromAxisAngle(axis, moveAngle);
quaternion.multiply(target);
// 移動
scene.children[index].position.x += -1 * w * Math.cos(Math.PI/6);
scene.children[index].position.y += h;
scene.children[index].position.z += w * Math.sin(Math.PI/6);
break;
こちらも回転は正四面体を表示させた時と同様です。
移動はy座標には移動高さ分を追加するのは先ほどと同じです。
x座標は移動幅分に正三角形の内角の半分(30°=$\pi/6$)のcosをかけたものに-1をかけたものを足します。(左に展開するため)
z座標は移動幅分に正三角形の内角の半分(30°=$\pi/6$)のsinをかけたものを足します。
for (let i = 0; i < 6; i++) {
openMesh(i);
}
底面以外の面に対して展開の処理を実行します。
面と線があるため、6回実行します。
return open;
展開処理を返却します。
(5)呼び出し処理(更新)
// 追加 START-----------------------------------
/** events */
document.getElementById('btnOpen').addEventListener('click', function() {
view.animationStatus['renderCanvas4Open'] = ANIM_STATUS_WAIT_START;
});
document.getElementById('btnReset').addEventListener('click', function() {
view.animationStatus['renderCanvas4Open'] = ANIM_STATUS_WAIT_RESET;
});
// 追加 END-------------------------------------
ボタンを押したときのイベントハンドラを追加します。
「animationStatus」プロパティの値を変更することにより、
動作指示を伝えています。
// 追加 START-----------------------------------
view.render('rp4Open', CANVAS_TYPE_RP4_OPEN);
// 追加 END-------------------------------------
表示先のキャンバスのidを指定して正四面体(展開)の描画処理を呼び出します。
(6)動作確認
ここまでのコードを書いたらブラウザで開いて次の確認をします。
- 展開用の正四面体が正しく表示されること
- 「展開」ボタンを押すと展開のアニメーションが始まること
- 「リセット」ボタンを押すと元の状態に戻ること
最後に
ここまでお付き合いいただきましてありがとうございました。
今回は計算部分の考え方をきちんと伝えたかったことと、一つの記事にしては非常に長いソースコードのため読むだけでも大変だったかと思います。
本記事に掲載したコードを書くのに次のサイト様の情報を参考にさせていただきました。
Three.js入門サイト
https://ics.media/tutorial-three/
Three.jsで立方体を転がすサンプルを作ろう
https://qiita.com/MasaoBlue/items/1ff943dde6ab5f53ef02
three.jsは非常に強力な3D描画ツールです。
これを用いて得られる知識はweb上での3D描画だけではなく、3DアプリやVRなどにおいても非常に有用に感じました。
有用なだけでなく実装しているのも楽しいので、これからもより理解を深めてもっと扱えるようになりたいと思います。
以上です。
この記事が3D描画に興味をお持ちの方の助力になれば幸いです。