ボルダリングの安定性をロボット工学で考えてみる

この記事は東京大学航空宇宙工学科/専攻 Advent Calendar 2019の10日目の記事として書かれています。昨年の同カレンダーではイベントカメラの話という記事を書きました。なんか地味にリアクションが多くて嬉しい限りです。

今回の内容

最近ボルダリングにはったのですが、やっぱり安定性が重要なので力とかモーメントのつり合いを（定性的に？）考えることが多いです。まあつまり力学なわけです。

実は今すこしだけ留学してロボット工学を勉強しているのですが、ロボット工学で登場する力学がこれに近いことをしているような気がしたので、ボルダリングをロボット工学（実質力学だけど）で考えてみようと思います。

ボルダリングとは

まあ皆さんボルダリングの壁くらいはみたことあると思いますが、下の画像のように壁についているホルダーを上手く使いながら壁を登るスポーツです。個人的には、上達っぷりが目に見えてわかること、周りの人とどう登るかを議論したりワイワイしたりしながら楽しむことができるのでハマっています。
実は筋力は（特に難しい課題でなければ）あまり必要では無く、それよりも手足や重心をどう配置してどの方向に力を入れれば安定して登れるのかという「力学的な安定性」を考えなければ上手く登ることができるができません（ボルダリング問題とここでは呼ぶことにします）。ちゃんと考えないと手足が滑ったり次のホルダーに手が届かなかったりしてうまく登れません。

ゼロモーメント点 (ZMP)

多分似ていると思われるのが、脚付きロボットの安定性の指標として用いられる**ゼロモーメント点(ZMP)**というものが近いかもしれません。

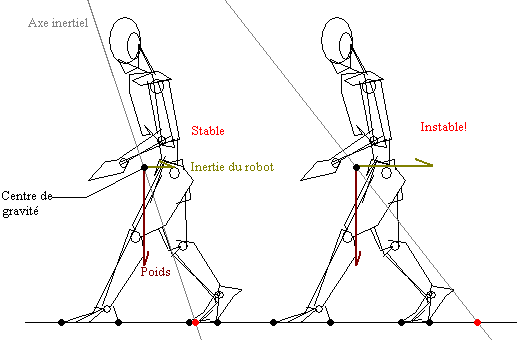
平面に立っている歩行ロボット（動物でも可）にはたらく重力と慣性力との合力が地面と交差する点がZMPです。航空力学でいう風圧中心的なやつですかね。慣性力を考慮しているあたりからも分かる通りロボットが動いている間の安定性も解析することができます。

ZMPでは不十分？

ZMPは、ロボットの接地面が水平なら良いのですが、実は水平ではなく**「滑り」を考慮しなければいけない場面では不十分**です。というのもZMPは摩擦が十分にあることを仮定していて、手足が滑るかどうかを判定することはできません。

ボルダリングでは、手足がホルダーから滑らないようにしっかりと垂直抗力をかける必要があります。経験者ならわかると思いますが（というか考えれば当たり前ですが）ホルダーの面に対してなるべく垂直に力をかけないとルートによってはすぐに滑ってしまいます。

ZMPは、手足のついたロボットや動物の安定性を数学的に扱えるという点でボルダリング問題に使えると思うのですが、滑りを考慮できないので拡張が必要そうです。

CWCへ拡張

とある論文で ¹ Contact Wrench Cone (CWC)というものが提案されています。ロボットの安定性を「レンチ$\mathbf{w}=(f,\tau)^T \in \mathbb{R}^6$が特定の領域（=CWC）内に入っていること」という条件として書き下すことができます。$f,\tau$はそれぞれロボットに作用している力とモーメントです。ちなみに接地面が水平なときはZMPと等価らしい ²です。

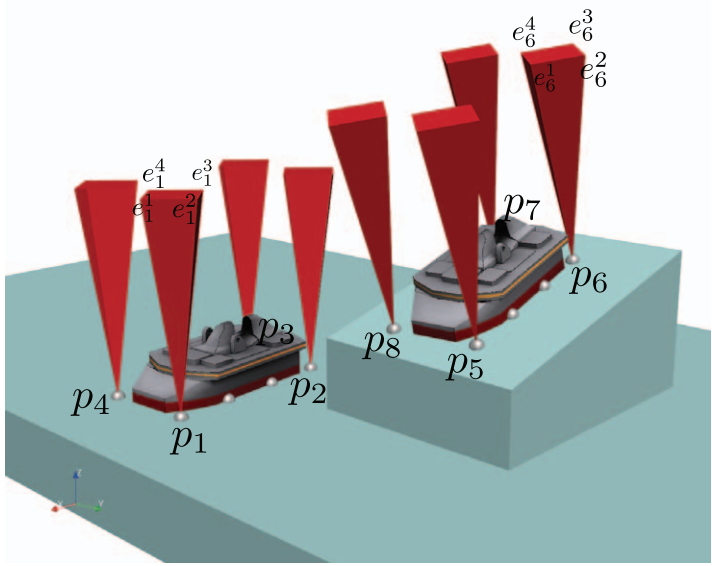
上の「特定の領域内」は6次元なので図示するのが難しいんですが、最初の3次元分だけ図示すると下図のようになります。接地点ごとにコーン状の領域を定義することができ、その積集合が上で言うCWCとなります。つまり、「ロボットにはたらいている力とトルクが下図のようなコーン内に入っている」ことが確認できればその状態は安定だということができるわけです。ボルダリングで言い換えれば

自分にはたらく力とトルクから定義されるレンチが、手足の接地点から定義されるCWC内にあれば安定である

というわけです。

ようするに

こんなこと考えないでもなんとなーく学習してスルスル登れる人間ってすごいですね。

...とあるきっかけでこの辺りに関する論文を読んでいて、ふとボルダリングにおける安定性の評価に使えるのではないかと思って書いたのですが、締め切りまであまり時間が取れず、にわか丸出しの内容スカスカ系記事になってしまいました、、、。というか内容が間違っている可能性もあるので誰か専門の人いたら教えてください。

留学のことについて書こうとも思ったのですが、僕よりインパクトのある（と期待される）南アフリカ留学体験記がこのカレンダーの後ろに控えているので気が引けたのと、特に航空と関係ないことなのでやめました。そして留学中にはまったボルダリングについて書こうと思い書いて見ましたが結局航空関係なくなりました。おわり。

1. Hongkai Dai and Russ Tedrake. Planning robust walking motion on uneven terrain via convex optimization. In IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), 2016. ↩

2. H Hirukawa, S Hattori, K Harada, S Kajita, K Kaneko, F Kanehiro, K Fujiwara, and M Morisawa. A universal stability criterion of the foot contact of legged robots - Adios ZMP. Proc. of the IEEE Int. Conf. on Robotics and Automation, 2003. ↩