（私のような）猿でもわかる強化学習（Q学習）

はじめに

一度、DQNを通してお勉強したのですが、いまいち納得できていなかったので、ちゃんと勉強し直します。
とは言っても、変数とか数式とか出てくると意識が飛んでしまうので、なるべく簡単な言葉に翻訳します。

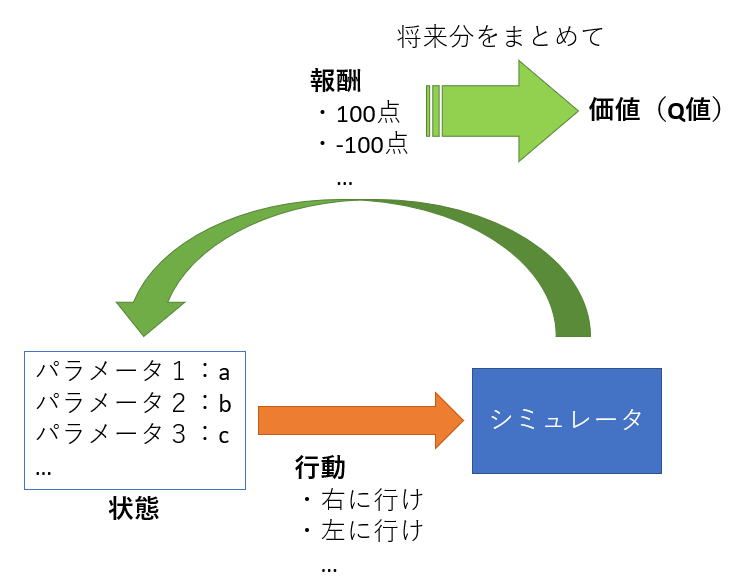
登場人物（ひとではない）

• 状態
  • 今どういう環境になっているのか
• 行動
  • 今の状態から何をするのか
• 報酬
  • 行動したことによりもらえるお金（のようなもの）
• 価値（Q値）
  • 将来の報酬を集めたもの

ゴール

ある状態でどういった行動をとれば、価値（Q値）が最大になるのかを求める。
瞬間瞬間で、常にベストな行動をとるイメージです。

基本的な考え方

今の状態である行動をとったときの価値（Q値）は、それによってもらえる報酬と、その後の価値（Q値）を足したものになります。

価値（Q値）＝報酬＋その後の価値（Q値）

ただし、その後の価値（Q値）は確定ではないので、正確にはちょっと割り引いた値（割引率）にします。
（この説明では、話を簡単にするために省略）

価値（Q値）の求め方

価値（Q値）の求め方はいろいろあります。

• Q学習
• SARSA
• モンテカルロ法
• etc.

ここでは「Q学習」での求め方を説明します。

Q学習

残念ながら将来の価値（Q値）はわかりませんので、実際に「ある状態のときにある行動をとったらいくらの報酬になった」かを学習して、どんどん価値（Q値）を更新することで実現します。

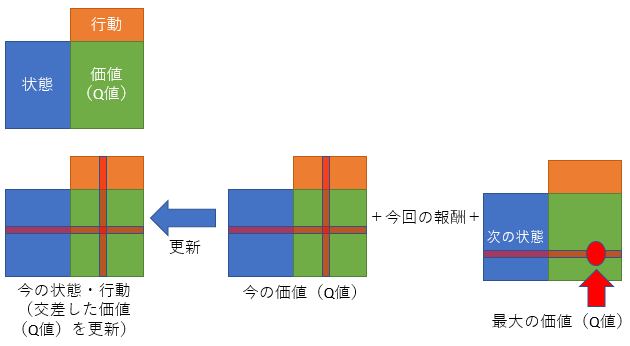
今の価値（Q値）を、更新前の今の価値（Q値）と、今回の行動によって得られる報酬と、次の全ての行動の価値（Q値）の最大値を足したものとするのがQ学習になります。
次に行う行動はわからないので、とりあえず最大値を使用するという、ざっくりとした計算でも大丈夫そうです。
なお、「次の全ての行動の価値（Q値）」も更新前の値を使用します。

今の価値（Q値）＝更新前の今の価値（Q値）
　　　　　　　　＋（今回の報酬＋次の全ての行動の価値（Q値）の最大値）

また、本当はそこに学習率をかけることで、どのくらい急激に価値（Q値）を変化させるかを指定します。
（この説明では、話を簡単にするために省略）

この計算を、実際に学習するときに行い、価値（Q値）を更新していきます。

最終的に、状態×行動のマトリックスに価値（Q値）を設定した表が出来上がります。
※今の状態と行動から報酬が求められるので、それと表の価値(Q値)を使って、表を更新していきます

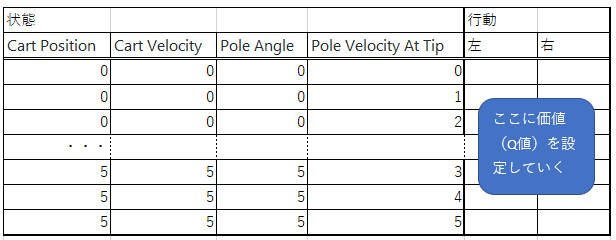
※OpenAIの「CartPole v0」で、状態を6種類に量子化した場合

図解

価値（Q値）の更新を、簡単なポンチ絵で説明してみます。

実行

出来上がった表に従い、今の状態から、価値（Q値）が最大となる行動を選んでいけば、最適な行動がとれるということになります。

問題点

一見なんの問題もなさそうな仕組みですが、状態のパターンが多い（離散的ではなく連続的な場合とか）と、表が作れないという問題があります。
（学習できなかったパターンがあると、正しく価値（Q値）が求められない）
そこで、機械学習（Deep Learning）を使って価値（Q値）を近似してしまおうというということになります。

なので、次はDQN（Deep Q-Network）をこのくらい簡単に説明できればなと思っています。