はじめに
はじめましてこの度NTTドコモサービスイノベーション部アドベントカレンダー21日目を担当させていただく三村と言います.
今年もドコモの有志でAdventCalendarを書くことになったので、記事を書きたいと思います。
いきなりですが、回帰問題ってご存知でしょうか?回帰問題は株価の予想などいろいろなところで使われる問題です。
ドコモでも様々なところでこの回帰問題を扱っています。
本記事でははこの回帰問題を解く手法の一つとしてガウシアンプロセス回帰があり、これを実装していこうと思います。今回の目的はnumpyで実装することであり理論的な説明ではありませんよろしくお願いします。
この辺の具体的な内容を知りたい方は「ガウス過程と機械学習 (機械学習プロフェッショナルシリーズ) 」 を呼んでください
また、実際にいろいろとガウシアンプロセスを使う人はGPyTorchやGPyを使いましょう!最後に今回はカーネル関数の最適化やパラメータ調整はできていません。ごめんなさい…
回帰問題を解く手法の簡単な説明について
回帰問題の簡単とは簡単にいうと、「ある観測できるデータ$X$から何かのデータ$Y$を予測したい」という問題です。
この問題を解く手法として$y=Ax+B$のような関数を用意する方法があります。こうすることである変数$x_i$を観測できれば$y_i$を予測することができます。
しかし現実には$y=Ax+B$のような簡単な関数で表現することは難しいです。これを解決する方法として$y=Ax^2+Bx+C$のように式を難しくして表現力を上げることを行います。
今回はこの複雑にした関数を$y = W^T \phi(x)$と表現します。例えば$W=[A,B,C],\phi(x)=[x^2,x^1,x^0]$とすればうまく$y=Ax^2+Bx+C$を表現することができます。
つまり$\phi(x)$を難しくしていきこれに対する$W$を求めることができればうまく$Y$を予測することができます!!!!
やったー!!!!!!!!!!!!!!!!!!!
…
ここで終わったら題目に反してしまうのでここからガウス過程について説明します。
ガウス過程の簡単な説明について
まず初めに$y = W^T \phi(x)$の$\phi(x)$をガウス分布にすることを考えてみましょう。つまり$\displaystyle \phi(x)=\exp(-\frac{(x-\mu_h)^2}{\sigma})$にしてみるということです。これでも回帰問題は解くことはできます。
しかしこの手法では次元の呪いで計算量が膨大なことになってしまいます。この問題を解決するために$W$で期待値をとってモデルから積分消去する方法を考えます。
$y=\Phi W$として$w$が平均$0$、分散$\lambda^2 I$のガウス分布から生成されていると$w \sim N(0,\lambda^2 I)$となります。これは$y$が「ガウス分布に従う$W$を定数行列$\Phi$で線形変換したもの」であることを意味します。
このとき期待値と共分散は
-
$E[y]=E[\Phi W]=\Phi E[ww^T]=0$
-
$\Sigma = E[yy^T]-E[y]E[y]^T=E[(\Phi w)(\Phi w)^T]=\Phi E[ww^T]\Phi^T=\lambda^2\Phi\Phi^T$
となります
この結果から$y$は$y\sim N(0,\lambda^2\Phi\Phi^2)$の多変量ガウス分布に従うということになるのです。
$K=\lambda^2\Phi\Phi^T$とし$K_{n,n'}=\lambda^2\phi(X_n)\phi(X_{n'})$としさらに$y$の平均を$0$になるように正規化すれば$y\sim N(0,K)$になります。
これでもまだ$K_{n,n'}=\phi(X_n)\phi(X_{n'})$の計算が重たいですね...。しかしここであの有名な「カーネルトリックを使いましょう!」となります。これは$\phi(X_n)$を頑張って計算しなくても$K_{n,n'}$が計算できれば良いという考え方です。
ここまでくるともうひといきデータを
D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\} \\
とおきこれを元に学習し、新しいデータ$x^{new}$を観測した時$y^{new}$がどうなるかという$y^{new}=w^T\phi(x^{new})$を解けば良いだけです。
これを実現するために$y'=(y_1,y_2,\cdots,y_N,y^{new}),X=(x_1,x_2,\cdots,x_N,x^{new})$とすれば$y\sim N(0,K')$になります。
こうすると
\begin{pmatrix}
y \\
y^{new}
\end{pmatrix}
\sim
N\left(0,\begin{pmatrix}
K,k_{new} \\
k_{new}^T,k_{new,new}
\end{pmatrix}\right)
と書くことができます。ここで$k_{new},k_{new,new}$はそれぞれ下記の通りです。
\left\{
\begin{array}{}
k_{new} &=(k(x^{new},x_1),k(x^{new},x_2),\cdots,k(x^{new},x_N))^T \\
k_{new,new}&= (k(x^{new},x^{new}))
\end{array}
\right.
ここで
\begin{pmatrix}
y_1 \\
y_2
\end{pmatrix}
\sim N\left(
\begin{pmatrix}
\mu_1 \\
\mu_2
\end{pmatrix}
,
\begin{pmatrix}
\Sigma_{1,1},\Sigma_{1,2} \\
\Sigma_{2,1},\Sigma_{2,2}
\end{pmatrix}
\right)
という式があった時、$p(y_2|y_1)$を$p(y_2|y_1)=N(\mu_2+\Sigma_{2,1}\Sigma_{1,1}^{-1}(y_1-\mu_1),\Sigma_{2,2}-\Sigma_{2,1}\Sigma_{2,1}^{-1}\Sigma_{1,2})$ で表現できるということが知られています。今回は$\mu_1=0,\mu_2=0$なので$p(y_2|y_1)=N(\Sigma_{2,1}\Sigma_{1,1}^{-1}y_1,\Sigma_{2,2}-\Sigma_{2,1}\Sigma_{2,1}^{-1}\Sigma_{1,2})$で表現できます。
ここまで長かったですがつまり
p(y^{new}|X^{new},D)=N(k_{new}^TK^{-1}y,k_{new,new}-k_{new}^TK^{-1}k_{new})
を実装すればよいということです!!!
実際に実装していこう!
p(y^{new}|X^{new},D)=N(k_{new}^TK^{-1}y,k_{new,new}-k_{new}^TK^{-1}k_{new})
さきほどこれを実装すれば良いということがわかりました。
↓↓↓↓↓↓↓ あなたの記事の内容
また$K,k_{new},k_{new,new}$は
───────
また $K$,$k_{*}$,$k_{**}$は
↑↑↑↑↑↑↑ 編集リクエストの内容
\left\{
\begin{array}{}
K &=\left[\begin{array}{}
k(x_1,x_1),k(x_1,x_2),\cdots,k(x_1,x_N) \\
k(x_2,x_1),k(x_2,x_2),\cdots,k(x_2,x_N) \\
\cdots \\
k(x_N,x_1),k(x_N,x_2),\cdots,k(x_N,x_N)
\end{array}
\right] \\
k_{new} &=(k(x^{new},x_1),k(x^{new},x_2),\cdots,k(x^{new},x_N))^T \\
k_{new,new}&= (k(x^{new},x^{new}))
\end{array}
\right.
でした。
k(x,x')=\theta_1\exp \left(-\frac{(x-x')^2}{\theta_2}\right)+\theta_3\delta(x,x')
とするとカーネル関数は
def RBF(X,X_):
theta_1 = 1
theta_2 = 0.2
theta_3 = 0.01
distance = ((X - X_)**2).sum(-1)
if distance.shape[0] == distance.shape[1]:
return theta_1 * np.exp(-1 * distance/theta_2) + theta_3 * np.eye(len(X))[:,:X.shape[1]]
else:
return theta_1 * np.exp(-1 * distance/theta_2)
で書くことができます。
↓↓↓↓↓↓↓ あなたの記事の内容
これを使って$K^{-1},k_{new},k_{new,new}$を計算していきましょう。
───────
これを使って$K^{-1}$, $k_{*}$, $k_{**}$を計算していきましょう。
↑↑↑↑↑↑↑ 編集リクエストの内容
まず$K^{-1}$を計算します。
X_ = np.array([X for _ in range(len(X))])
K = RBF(X_,X_.transpose(1,0,2))
inv_K = np.linalg.inv(K)
↓↓↓↓↓↓↓ あなたの記事の内容
次に$k_{new}$と$k_{new,new}$を計算します。
───────
次に$k_{*}$と$k_{**}$を計算します。
↑↑↑↑↑↑↑ 編集リクエストの内容
X__ = np.array([X for _ in range(len(Test_X))])
Test_X__ = np.array([Test_X for _ in range(len(X))]).transpose(1,0,2)
Test_X__a = np.array([Test_X for _ in range(len(Test_X))]).transpose(1,0,2)
k = RBF(X__,Test_X__)
k__ = RBF(Test_X__a,Test_X__a)
最後に
p(y^{new}|X^{new},D)=N(k_{new}^TK^{-1}y,k_{new,new}-k_{new}^TK^{-1}k_{new})
から生成するように
Y_result = np.random.multivariate_normal(k.dot(inv_K).dot(Y),k__ - k.dot(inv_K).dot(k.T))
とかけばよいです
ニューヨークのバイクシェアデータで実験
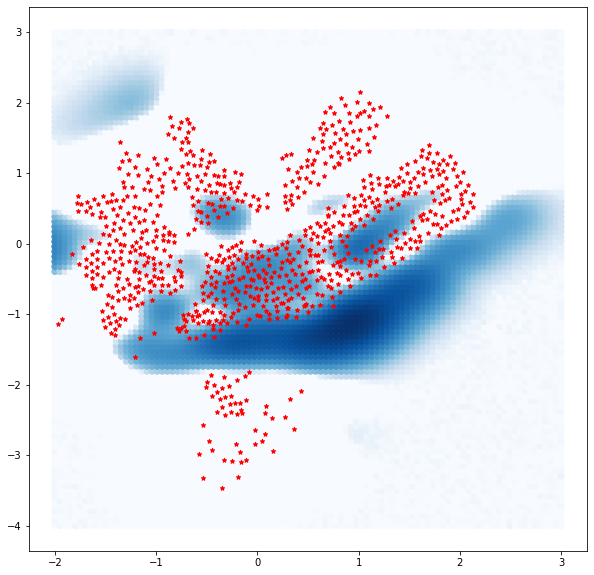
ニューヨークのバイクシェアデータを使って絵を予測してみましょう。
今回は6月30日の朝8時から昼12時までの自転車の返却された数で可視化してみました。
みやすいように返却された数に対して対数で正規化しています。
それではガウシアンプロセスを使って可視化してみましょう
するとこんな感じになります。
星がポートの位置です。
あと見やすいように$0$以下は$0$で補完しています。
結果から中心部に高い需要があることが見て取れます。
ポートがない位置は分散が大きいため色々な値がサンプリングされるため今回は高い需要がるように推論されました。
このようにガウシアンプロセスの良いところはデータがないところに対しても予測することができるだけでなくその部分の分散も計算できるところです。
最後に
こんな感じで回帰問題を解けるので皆さんも一度使ってみてはいかがでしょうか?