はじめに
「ハードダーツで得点計算をするシステムを作りたい!」
と言う目標を持ってプロジェクトを進めてみたが, なかなか課題も多くプログラミング初心者の私にはカメラ一つではうまく実装できないというのが現状である.
ところで, ダーツボードというのはかなり規則的な形をしている. そのもの自体は真円であり, その中心にはBULLというものが飾られているわけだ. その特性を利用し, 斜めから撮影したダーツボードをいかにも正面から撮ったみたいな写真(または動画)にしていきたいというのが今回の内容である.
これは意外と単純な話ではない(と思う). 例えば斜めから撮った画像をうまく淵が円になるようにAffine変換すると

こんな感じだ. 緑の線で描いた円とその中心がズレているのがわかるだろう.
ちなみにAffine変換についてはこの記事を参考にした.
Python, OpenCVで幾何変換(アフィン変換・射影変換など)
一方で今回のテーマの変換を用いれば

このように正面から撮ったような画像にすることができた.
以下ではこの変換自体について論じて, さらに実装も書いていきたいと考えている.
全二部構成(の予定)で, 今回は変換の理屈について論じ, 私の書いたコードの全体を提示したいと思う. 第二部ではコードの詳細を説明したい.
最終的にはリアルタイムに取得した斜めからのダーツボードのイメージを歪みなく中心が一致するように描画し続けるプログラムを与える.
私が使用したものと環境
- Raspberry Pi 4B / 4GB RAM
- raspi カメラモジュール / Pi Zero Camera
- Python 3.7.3
- Kivy 1.11.1
WebカメラとPython, Kivyの実行環境さえ整えれば上のものに縛らずともできると思います. Kivyはリアルタイム表示のGUIとして使用したので本質的に必要ではありません.
変換の理屈
特に図形的な処理をするのだが, 必要とするのは高校数学で扱ったような
- メネラウスの定理
- 3次元空間ベクトル
- 行列または複素平面を用いた座標の回転
このあたりの内容を含んでいて, あまり高度な処理は行なっていない.
さて, 楕円を含む画像を楕円画像, その座標系を楕円座標と呼ぶことにする. またそれを円に変換した時の座標系を円座標と呼ぶことにする. はじめに結論を述べるとその変換は適当な定数$a, h, \varphi$を用いて
\begin{align}
x_\mathrm{cir} &= \frac{x_\mathrm{ell}
(h + a\sin \varphi \cos \varphi) - a h \cos^2 \varphi}{x_\mathrm{ell} \cos \varphi + h \sin \varphi}\\
y_\mathrm{cir} &= \frac{y_\mathrm{ell}
(h \sin \varphi + a \cos \varphi)}
{x_\mathrm{ell} \cos \varphi + h \sin \varphi}
\end{align}
によって表される. ただしこの変換は座標の原点や軸の取り方に依存する.
ここからはこの式の意味を詳しく説明する.
まずダーツボードとそれを見ている観測者を模式的に表した次の図を考えよう.
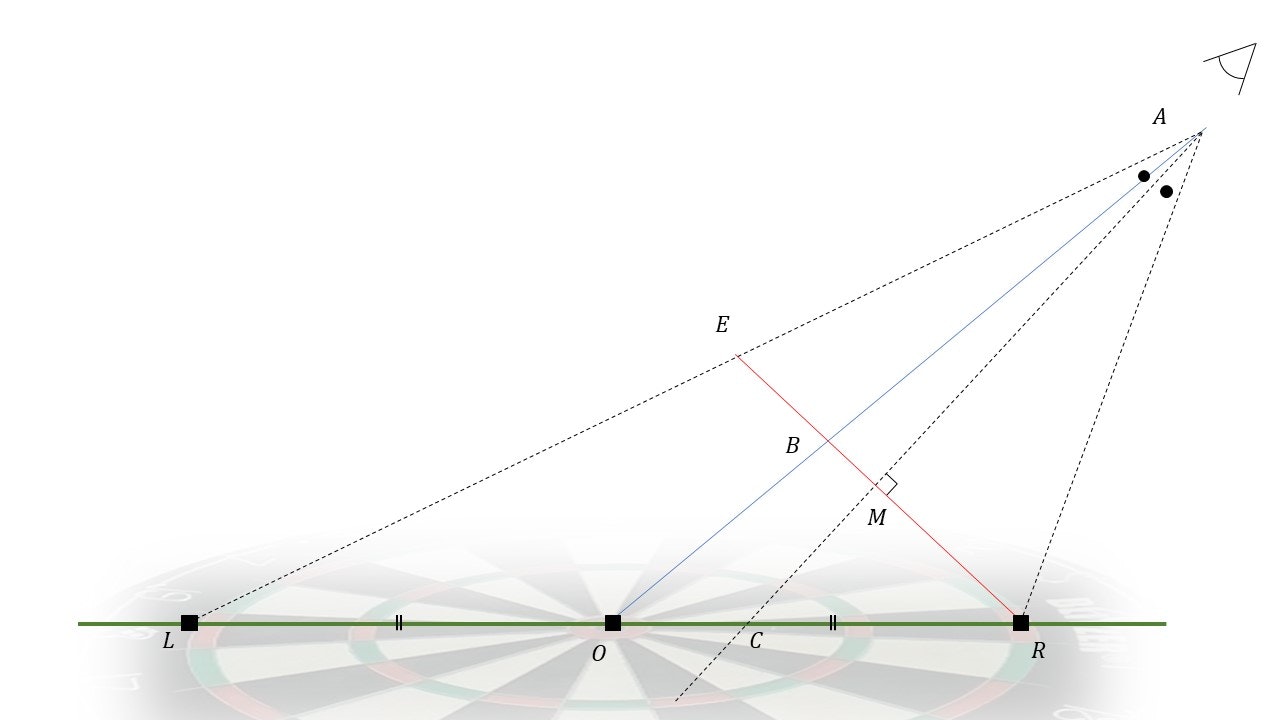
ここでは点$O$を実際のボードのBULL, 点$R$をボード上の観測者に最も近い点として点$A$から観測する状況を表している. 赤線で表されているのは観測者が見ている"見かけ上"のダーツボードが写し出されている平面である. すなわち, これは$\angle CAL = \angle CAR$として設定された直線$AC$に対して点$R$を通る垂直な平面である. これを見ると観測の赤線平面では歪みが発生し, BULLの位置である点$B$と中心$M$にズレが生じていることがわかる. この赤線が上での楕円座標に対応し, また緑の線が円座標に相当する.
まず次のパラメータがGivenである場合について.
a = RM, \quad h = AM, \quad \varphi = \angle ACR
特に計算を簡単にするために点$M$を原点とする3次元空間座標系を考える. 例えば代表的な点として座標を$M(0, 0, 0), A(h\cos \varphi, 0, h\sin \varphi), R(a \sin \varphi, 0, - a\cos \varphi)$と表すことができる.
この時赤線で表す平面は
(\cos \varphi) x + (\sin \varphi) z = 0
となる.
ここで緑線で表す平面上の点$P(x, y, - a \cos \varphi)$とすると
直線$AP$の点を$Q(X, Y, Z)$とすると適当な実数$t$を用いて
\begin{align}
\left(
\begin{array}{c}
X\\
Y\\
Z
\end{array}
\right)
=(1 - t)
\left(
\begin{array}{c}
x\\
y\\
- a \cos \varphi
\end{array}
\right) + t
\left(
\begin{array}{c}
h \cos \varphi\\
0\\
h \sin \varphi
\end{array}
\right)
\end{align}
とできる. これが赤線平面上にある時
\cos \varphi[(1 - t) x + th \cos \varphi]
+ \sin \varphi[- (1 - t) a \cos \varphi + t h \sin \varphi] = 0
従って
t = \frac{(a \sin \varphi - x)
\cos \varphi}{h + (a \sin \varphi - x) \cos\varphi}
これによって$Q(X, Y, Z)$が定まる. また$M$を中心に$(X, Z)$を$(\pi / 2 - \varphi)$回転させて得た値を$(x_\mathrm{ell}, y_\mathrm{ell}, 0)$とすると最終的な計算結果は
\begin{align}
x_\mathrm{ell} &= \frac{h(x \sin \varphi + a \cos^2 \varphi)}{h + (a \sin \varphi - x) \cos \varphi}\\
y_\mathrm{ell} &= \frac{h y}{h + (a \sin \varphi - x) \cos \varphi}
\end{align}
逆に$(x_\mathrm{ell}, y_\mathrm{ell})$から$(x, y)$を書くと
\begin{align}
x &= \frac{x_\mathrm{ell}(h + a \sin\varphi \cos \varphi) - ah \cos^2 \varphi}{x_\mathrm{ell} \cos \varphi + h \sin \varphi}\\
y &= \frac{y_\mathrm{ell} (h \sin \varphi + a \cos \varphi)}{x_\mathrm{ell} \cos \varphi + h \sin \varphi}
\end{align}
となってこれが上の$(x_\mathrm{cir}, y_\mathrm{cir})$に一致していることがわかる.
パラメータの決定方法
一方で楕円座標を表す画像データから$a, h, \varphi$のパラメータをどのように表すかについて論じる. まずデータとしては楕円画像を見るとBULL位置の楕円中心からのズレと楕円半短軸の長さの比がわかる.これを上の記法を用いて$\alpha = BM / RM$とする.
メネラウスの定理より次の三式が成立する.
\frac{LA}{AE}\cdot\frac{EB}{BR}\cdot\frac{RO}{OL}= 1, \:
\frac{LA}{AE}\cdot\frac{EM}{MR}\cdot\frac{RC}{CL}= 1,
\:
\frac{LR}{RC}\cdot\frac{CM}{MA}\cdot\frac{AE}{EL} = 1
一つ目の式を整理すると
\frac{LA}{AE} = \frac{1 + \alpha}{1 - \alpha}
となるから二つ目の式より
\frac{RC}{CL} = \frac{1 - \alpha}{1 + \alpha}
よって三つ目の式より
CM = \alpha h
が成立する. 緑線へ点$M$から垂線を下ろせば
CR = CM \cos \varphi + RM \sin \varphi
= \alpha h \cos \varphi + a \sin \varphi
また垂線は大きさが一致するから
\alpha h \sin \varphi = a \cos \varphi
ここで$CR: CL$比から
OR = \frac{1}{1 - \alpha}(\alpha h \cos \varphi + a \sin \varphi)
一方で直線$RE$に垂直な平面で点$M$を通るものを考えると次の図のようになる.
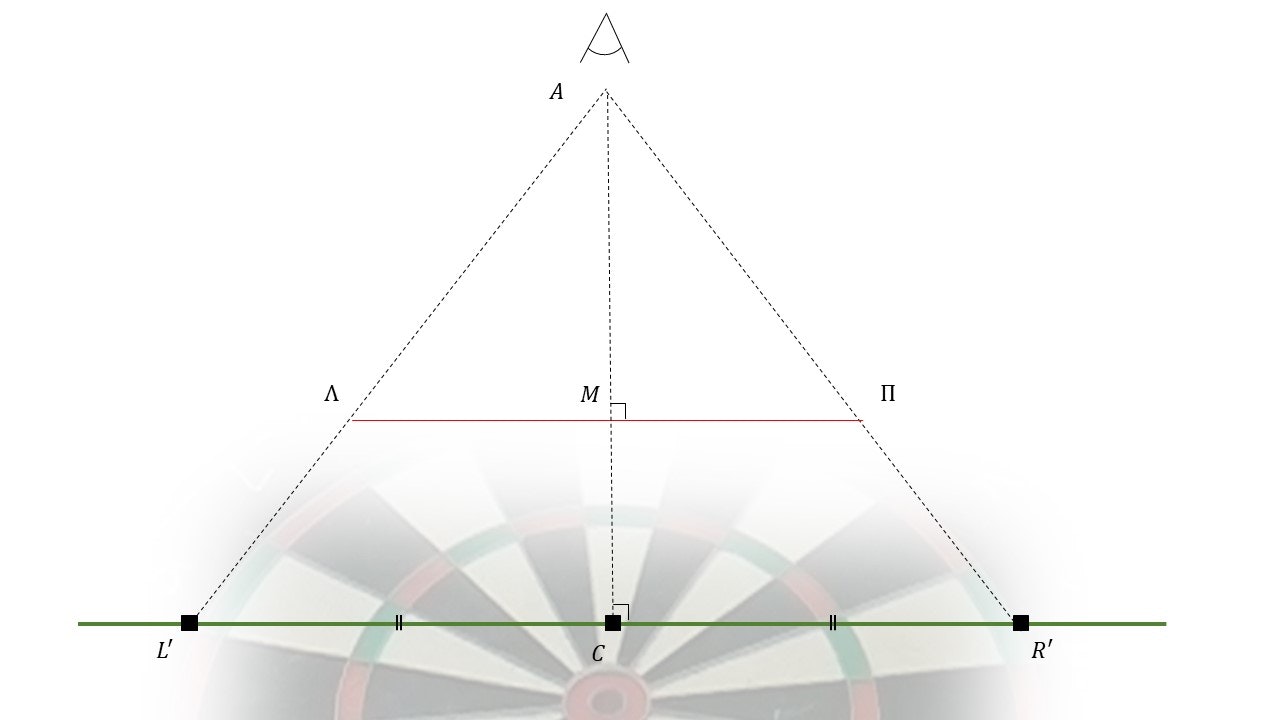
b = \Pi M = \Lambda M
と設定すると相似図形より
CR^\prime = (1 + \alpha) b
また対称性より$\angle OCR^\prime = \angle OCL^\prime = 90^\circ$となるから三平方の定理より
(OR^\prime)^2 = (OC)^2 + (CR^\prime)^2
さらに, 元のダーツボードが真の円形であると仮定し$OR = OR^\prime$とすれば
\sin \varphi = \frac{a}{b} \cdot \frac{1}{\sqrt{1 - \alpha^2}}
長さを表す変数を$a$で割ることで無次元化し$x^a = x / a$のように表すと
\begin{align}
h^a &= \frac{1}{\alpha \tan \varphi}\\
x_\mathrm{cir}^a &= \frac{x_\mathrm{ell}^a(h^a + \sin\varphi \cos \varphi) - h^a \cos^2 \varphi}{x_\mathrm{ell}^a \cos \varphi + h^a \sin \varphi}\\
y_\mathrm{cir}^a &= \frac{y_\mathrm{ell}^a (h^a \sin \varphi + \cos \varphi)}{x_\mathrm{ell}^a \cos \varphi + h^a \sin \varphi}
\end{align}
とできることから本質的には$\alpha$と$a: b$の比がわかれば, 上で与えたパラメータが決定でき, 楕円座標と円座標の変換を与えられることが言える. また以下のコードでも記述される通り, 取り込んだイメージデータからダーツボードの楕円とBULLから全体に放射状に伸びる線分さえ検出できれば$\alpha, a: b$を決定することができる.
実際に書いたコード
# -*- coding: utf-8 -*-
from kivy.config import Config
Config.set('graphics', 'width', '1024')
Config.set('graphics', 'height', '512')
from kivy.app import App
from kivy.graphics.texture import Texture
from kivy.graphics import Line
from kivy.uix.widget import Widget
from kivy.uix.behaviors import ButtonBehavior
from kivy.uix.image import Image
from kivy.clock import Clock
from kivy.properties import ObjectProperty
import cv2
import numpy as np
import board_analysis as ba # 自作のモジュール
captured_image = cv2.VideoCapture(0)
# 取得する画像の大きさを指定
captured_image.set(cv2.CAP_PROP_FRAME_WIDTH, 511)
captured_image.set(cv2.CAP_PROP_FRAME_HEIGHT, 511)
class CameraViewing(Image):
def __init__(self, **kwargs):
super(CameraViewing, self).__init__(**kwargs)
# 0番目のカメラに接続
self.capture = captured_image
# 描画のインターバルを設定
Clock.schedule_interval(self.update, 0.2)
# インターバルで実行する描画メソッド
def update(self, dt):
# フレームを読み込み
ret, self.frame = self.capture.read()
# Kivy Textureに変換
buf = cv2.flip(cv2.rotate(self.frame, cv2.ROTATE_90_COUNTERCLOCKWISE), 0).tobytes()
texture = Texture.create(size=(self.frame.shape[0], self.frame.shape[1]), colorfmt='bgr')
texture.blit_buffer(buf, colorfmt='bgr', bufferfmt='ubyte')
# インスタンスのtextureを変更
self.texture = texture
class TransformedViewing(Image):
def __init__(self, **kwargs):
super(TransformedViewing, self).__init__(**kwargs)
self.capture = captured_image
self.frame = np.zeros((512, 512, 3))
# 描画のインターバルを設定
Clock.schedule_interval(self.update, 0.2)
# インターバルで実行する描画メソッド - dt に一回画像を描画する.
def update(self, dt):
try:
# フレームを読み込み
ret, bgr = self.capture.read()
imCal = ba.BoardPicture(bgr)
# 楕円を検出し, その情報の書き込み
ellipse = ba.findEllipse(imCal.contours, 100000, 250000)
# 直線データを検出
lines = cv2.HoughLines(imCal.edge, 1, np.pi / 80, 100)[:, 0, :]
# 直線データの中で楕円の中心付近を通るものを一つ選択
ellipse.seg_line(lines)
# 楕円空間上の各グリッドの座標
X_ell, Y_ell = np.meshgrid(range(512), range(512))
# 楕円空間と円空間の座標の対応関係を表す. xx, yy は円空間での対応座標.
x_cir, y_cir = ellipse.ellipse2circle(X_ell, Y_ell)
# 円空間上での中心座標
ox_cir, oy_cir = ellipse.ellipse2circle(ellipse.origin[0], ellipse.origin[1])
# 端を揃えるための処理
ox_cir = ox_cir - x_cir.min()
oy_cir = oy_cir - y_cir.min()
xint = (x_cir - x_cir.min()).astype(np.int64)
yint = (y_cir - y_cir.min()).astype(np.int64)
width = x_cir.max() - x_cir.min()
height = y_cir.max() - y_cir.min()
imcircle = np.zeros((int(height) + 1, int(width) + 1, 3), np.uint8)
# イメージの書き込み
imcircle[yint, xint, :] = bgr[:, :, :]
l1 = 310
frame = imcircle[int(oy_cir) - l1: int(oy_cir) + l1, int(ox_cir) - l1: int(ox_cir) + l1, :]
frame = cv2.resize(frame, (512, 512))
frame = ba.gamma_correction(frame, 0.5)
kernel = np.ones((5, 5), np.float32) / 25.
self.frame = cv2.filter2D(frame, -1, kernel)
# Kivy Textureに変換
buf = cv2.flip(self.frame, 0).tobytes()
texture = Texture.create(size=(self.frame.shape[0], self.frame.shape[1]), colorfmt='bgr')
texture.blit_buffer(buf, colorfmt='bgr', bufferfmt='ubyte')
# インスタンスのtextureを変更
self.texture = texture
except:
buf = cv2.flip(self.frame, 0).tobytes()
texture = Texture.create(size=(self.frame.shape[0], self.frame.shape[1]), colorfmt='bgr')
texture.blit_buffer(buf, colorfmt='bgr', bufferfmt='ubyte')
# インスタンスのtextureを変更
self.texture = texture
class MainScreen(Widget):
def __init__(self, **kwargs):
super(MainScreen, self).__init__(**kwargs)
pass
class Camera_DrawingApp(App):
def build(self):
return MainScreen()
# return DrawInput()
if __name__ == "__main__":
Camera_DrawingApp().run()
# -*- coding: utf-8 -*-
import numpy as np
import cv2
class Ellipse():
def __init__(self, center, axis, angle_rad):
self.center = center
self.axis = axis # (短軸, 長軸)の順の長さ
self.angle = angle_rad
self.ellipse = (center, axis, angle_rad * 180. / np.pi)
# ダーツの原点座標 (origin) および原点と中心に関する比 (alpha) を出す
def seg_line(self, lines):
elm = len(lines)
a_ell, b_ell = self.axis
a = 0.5 * a_ell
b = 0.5 * b_ell
for i in range(elm - 1):
rho0, theta0 = lines[i]
for j in range(i + 1, elm):
rho1, theta1 = lines[j]
if abs(theta1 - theta0) > np.pi / 10:
break
o1 = ( np.sin(theta1) * rho0 - np.sin(theta0) * rho1) / np.sin(theta1 - theta0)
o2 = (- np.cos(theta1) * rho0 + np.cos(theta0) * rho1) / np.sin(theta1 - theta0)
alpha = np.sqrt((self.center[0] - o1) * (self.center[0] - o1)
+ (self.center[1] - o2) * (self.center[1] - o2)) / a
# 得られた直線が原点を通っているための必要条件
if alpha < np.sqrt(1 - a * a / (b * b)):
self.origin = (o1, o2)
self.alpha = alpha
return
# 楕円空間の点 (X, Y) を円空間の座標 (x, y) に変換する
def ellipse2circle(self, X, Y):
try:
a_ell, b_ell = self.axis
a = 0.5 * a_ell
b = 0.5 * b_ell
eps = a / b
sinphi = eps / np.sqrt(1 - self.alpha * self.alpha)
cosphi = np.sqrt(1 - sinphi * sinphi)
h = a * cosphi / self.alpha / sinphi
r = a / (1 - self.alpha) / sinphi
c = r * (cosphi / h) * (h * cosphi + a * sinphi)
X1 = np.cos(self.angle) * (X - self.center[0]) + np.sin(self.angle) * (Y - self.center[1])
Y1 = - np.sin(self.angle) * (X - self.center[0]) + np.cos(self.angle) * (Y - self.center[1])
x = (X1 * (h + a * sinphi * cosphi) - a * h * cosphi * cosphi) / (X1 * cosphi + h * sinphi) + c
y = (Y1 * (h * sinphi + a * cosphi)) / (X1 * cosphi + h * sinphi)
return (x, y)
except:
print("The lack of ellipse data!")
# 面積が範囲内の楕円形を見つける.
# contoursは点集合 - つなげると閉曲線.
def findEllipse(contours, minThresE, maxThresE):
for cnt in contours:
try:
Area = cv2.contourArea(cnt)
if minThresE < Area < maxThresE:
ellipse = cv2.fitEllipse(cnt)
# cv2.ellipse(image_proc_img, ellipse, (0, 255, 0), 2)
x, y = ellipse[0]
a_ell, b_ell = ellipse[1]
angle = ellipse[2]
center_ellipse = (x, y)
angle_rad = angle * np.pi / 180
return Ellipse(center_ellipse, (a_ell, b_ell), angle_rad)
except:
print("error")
class BoardPicture():
kernel1 = np.ones((5, 5), np.float32) / 25.
kernel2 = np.ones((3, 3), np.uint8)
def __init__(self, imCalBGR):
self.bgr = imCalBGR
self.hsv = cv2.cvtColor(self.bgr, cv2.COLOR_BGR2HSV)
blur = cv2.filter2D(self.hsv, -1, BoardPicture.kernel1)
h, s, imCal = cv2.split(blur)
ret, thresh = cv2.threshold(imCal, 50, 255, cv2.THRESH_BINARY_INV)
thresh2 = cv2.morphologyEx(thresh, cv2.MORPH_CLOSE, BoardPicture.kernel2)
self.thr = cv2.morphologyEx(thresh2, cv2.MORPH_OPEN, BoardPicture.kernel2)
self.edge = cv2.Canny(thresh, 250, 255)
# ダーツボードの中の閉曲線を contours として得る
self.contours, hierarchy = cv2.findContours(self.thr, 1, 2)
def gamma_correction(imCal, gamma):
table = 255 * (np.arange(256) / 255) ** gamma
table = np.clip(table, 0, 255).astype(np.uint8)
return cv2.LUT(imCal, table)
<MainScreen>:
BoxLayout:
orientation: 'horizontal'
size: root.size
CameraViewing:
size_hint_x: 0.5
TransformedViewing:
size_hint_x: 0.5
Kivyについては
Python Kivyの使い方① ~Kv Languageの基本~
Python KivyでWebカメラの映像を表示・撮影する【GUI】
このあたりを参考にした.
詳しい内容については次回の投稿に記述する.
ところでこれらの計算をできるようなライブラリがすでに存在してたりしますかね?もしご存じの方がいらっしゃいましたらコメントお願いします.