LoginSignup
37
31

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@mikecat_mixc

PNGで使うCRC32を計算する

Posted at

はじめに

この記事では、1バイト = 8ビットとします。

CRCとは

CRCは巡回冗長検査(Cyclic Redundancy Check)とも呼ばれ、データの破損を検出するためのチェックディジットの一種です。
基本的には、以下の手順で計算できます。

  1. 計算に使用するマジックナンバーを決める
  2. CRCの値を格納する変数を0で初期化する
  3. データのバイト列(ビット列)をCRCの値に下から順番にシフトし、流し込んでいく
  4. シフトしたときに上からあふれたのが1ならCRCの値にマジックナンバーをXORし、0ならXORしない

参考 : ContentsCRC
巡回冗長検査 - Wikipedia

初期化直後の状態

   CRCの値                            データ(ASCIIで「IEND」)
  +---------------+---------------+  +---------------+---------------+---------------+---------------+
  |0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|<-|0 1 0 0 1 0 0 1|0 1 0 0 0 1 0 1|0 1 0 0 1 1 1 0|0 1 0 0 0 1 0 0|
  +---------------+---------------+  +---------------+---------------+---------------+---------------+

   マジックナンバー 0x1021
  +---------------+---------------+
  |0 0 0 1 0 0 0 0|0 0 1 0 0 0 0 1|
  +---------------+---------------+

データを1ビットシフトする

   CRCの値                            データ
  +---------------+---------------+  +-------------+---------------+---------------+---------------+
  |0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|<-|1 0 0 1 0 0 1|0 1 0 0 0 1 0 1|0 1 0 0 1 1 1 0|0 1 0 0 0 1 0 0|
  +---------------+---------------+  +-------------+---------------+---------------+---------------+

データをもう1ビットシフトする

   CRCの値                            データ
  +---------------+---------------+  +-----------+---------------+---------------+---------------+
  |0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 1|<-|0 0 1 0 0 1|0 1 0 0 0 1 0 1|0 1 0 0 1 1 1 0|0 1 0 0 0 1 0 0|
  +---------------+---------------+  +-----------+---------------+---------------+---------------+

もう14ビットシフトする

   CRCの値                            データ
  +---------------+---------------+  +---------------+---------------+
  |0 1 0 0 1 0 0 1|0 1 0 0 0 1 0 1|<-|0 1 0 0 1 1 1 0|0 1 0 0 0 1 0 0|
  +---------------+---------------+  +---------------+---------------+

もう1ビットシフトする

   CRCの値                            データ
  +---------------+---------------+  +-------------+---------------+
  |1 0 0 1 0 0 1 0|1 0 0 0 1 0 1 0|<-|1 0 0 1 1 1 0|0 1 0 0 0 1 0 0|
  +---------------+---------------+  +-------------+---------------+

もう1ビットシフトすると、1があふれた

   CRCの値                            データ
  +---------------+---------------+  +-----------+---------------+
  |0 0 1 0 0 1 0 1|0 0 0 1 0 1 0 1|<-|0 0 1 1 1 0|0 1 0 0 0 1 0 0|
  +---------------+---------------+  +-----------+---------------+

   マジックナンバー 0x1021
  +---------------+---------------+
  |0 0 0 1 0 0 0 0|0 0 1 0 0 0 0 1|
  +---------------+---------------+

そこで、CRCの値にマジックナンバーをXORする

   CRCの値                            データ
  +---------------+---------------+  +-----------+---------------+
  |0 0 1 1 0 1 0 1|0 0 1 1 0 1 0 0|<-|0 0 1 1 1 0|0 1 0 0 0 1 0 0|
  +---------------+---------------+  +-----------+---------------+

このような「データの最後までシフトして1があふれたらXORする」をデータの最後まで繰り返すと、CRCが計算できる

PNGで使うCRC32

RFC2083 PNG (Portable Network Graphics) Specification Version 1.0 を見てみましょう。

3.4. CRC algorithm

Chunk CRCs are calculated using standard CRC methods with pre and
post conditioning, as defined by ISO 3309 [ISO-3309] or ITU-T V.42
[ITU-V42]. The CRC polynomial employed is

  x^32+x^26+x^23+x^22+x^16+x^12+x^11+x^10+x^8+x^7+x^5+x^4+x^2+x+1

The 32-bit CRC register is initialized to all 1's, and then the
data from each byte is processed from the least significant bit
(1) to the most significant bit (128). After all the data bytes
are processed, the CRC register is inverted (its ones complement
is taken). This value is transmitted (stored in the file) MSB
first. For the purpose of separating into bytes and ordering, the
least significant bit of the 32-bit CRC is defined to be the
coefficient of the x^31 term.

Practical calculation of the CRC always employs a precalculated
table to greatly accelerate the computation. See Sample CRC Code
(Chapter 15).

どうやら0ではなく1に初期化して、各バイトはLSBから入れていくようです。
また、マジックナンバーのnビット目は多項式にx^nの項があれば1、なければ0とします。
すると、

 3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1
 1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0 9 8 7 6 5 4 3 2 1 0
+---------------+---------------+---------------+---------------+
|0 0 0 0 0 1 0 0|1 1 0 0 0 0 0 1|0 0 0 1 1 1 0 1|1 0 1 1 0 1 1 1|
+---------------+---------------+---------------+---------------+

となり、マジックナンバーは0x04C11DB7となります。
また、CRCのLSBはなぜか最上位ビットと定義されているので、ひっくり返す処理を入れます。

ちなみに、PNGのチャンクのCRC32は長さ情報は入れず、チャンク名とチャンクのデータのCRC32を計算する
(RFC2083 3.2. Chunk layout)ので、「IEND」のCRC32を計算するとAE426082になるはずです。
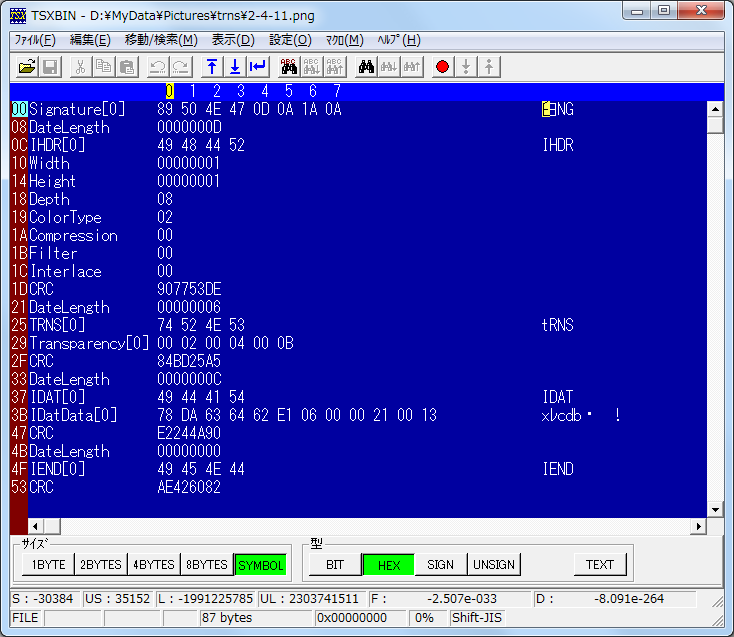
png-crc32-20160209.png
(使用ソフト : TSXBIN)

何も考えずに計算してみる (失敗)

何も考えずに上で説明したCRCの計算方法を実装してみましたが、650A9A55と出てきてしまい、うまくいきませんでした。

crc32test0.c
#include <stdio.h>
#include <inttypes.h>

uint32_t reverse(uint32_t x) {
  int i;
  uint32_t res = 0;
  for (i = 0; i < 32; i++) {
    if ((x >> i) & 1) res |= UINT32_C(1) << (31 - i);
  }
  return res;
}

int main(void) {
  const char *d = "IEND";
  uint32_t crc = UINT32_C(0xFFFFFFFF);        /* CRCの値 */
  uint32_t magic = UINT32_C(0x04C11DB7);      /* マジックナンバー */
  int i, j;
  for (i = 0; d[i]; i++) {                    /* データを前から後ろに処理していく */
    for (j = 0; j < 8; j++) {                 /* 各バイトをLSBから順に入れる */
      int b = !!(crc & UINT32_C(0x80000000)); /* 1があふれるかをチェックする */
      crc <<= 1;                              /* シフトする */
      if ((d[i] >> j) & 1) crc |= 1;          /* データのビットを入れる */
      if (b) crc ^= magic;                    /* 1があふれたらマジックナンバーをXORする */
    }
  }
  printf("%08"PRIX32"\n", reverse(~crc));
  return 0;
}

とりあえずまともに計算してみる

なぜ素直に計算しても値が合わなかったのでしょうか？
調べてみると、CRC32では

  • 最初は素直に0で初期化する
  • データの最初の4バイトをビット反転する
  • データの最後に4バイトの0x00を入れる

ということをしないといけないようです。

参考 : CRC-32

とりあえず、これをそのまま実装してみます。

crc32test1.c
#include <stdio.h>
#include <inttypes.h>

/* このバイトを処理した後のCRC32の値を計算する */
uint32_t crcnext(uint32_t crc, unsigned char d, uint32_t magic) {
  int i;
  for (i = 0; i < 8; i++) {                 /* LSBから順に処理する */
    int b = !!(crc & UINT32_C(0x80000000)); /* 上から1があふれるかをチェックする */
    crc <<= 1;                              /* シフトする */
    if ((d >> i) & 1) crc |= 1;             /* データのビットを入れる */
    if (b) crc ^= magic;                    /* 上から1があふれたらマジックナンバーをXORする */
  }
  return crc;
}

/* ビットをひっくり返す */
uint32_t reverse(uint32_t x) {
  int i;
  uint32_t res = 0;
  for (i = 0; i < 32; i++) {
    if ((x >> i) & 1) res |= UINT32_C(1) << (31 - i);
  }
  return res;
}

int main(void) {
  const char *d = "IEND";
  uint32_t crc = 0; /* 0で初期化する */
  uint32_t magic = UINT32_C(0x04C11DB7);
  int i, j;
  for (i = 0; d[i]; i++) {
    crc = crcnext(crc, d[i] ^ (i < 4 ? 0xFF : 0), magic); /* 最初の4バイトはビット反転する */
  }
  /* データの最後に4バイトの0x00を入れる */
  for (j = 0; j < 4; j++) {
    crc = crcnext(crc, i + j < 4 ? 0xFF : 0, magic);
  }
  printf("%08"PRIX32"\n", reverse(~crc));
  return 0;
}

すると、正しいAE426082という値を得ることができました。

reverse()関数を消す

とりあえず正しい値を求めることができましたが、reverse()関数の実装が適当なので、これをなんとかしたいです。
そもそも、こんな面倒くさいことをするのはやめてしまいましょう。
最後に反転するのではなく、計算の段階で反転させます。
マジックナンバーの値も反転させておきます。

反転前

   CRC32                                                              データ(LSBから先に入れる)
  +---------------+---------------+---------------+---------------+  +---------------+-
  |0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|0 1 1 0 1 1 0 1|<-|0 1 0 1 1 1 0 1|  ...
  +---------------+---------------+---------------+---------------+  +---------------+-

   マジックナンバー (0x04C11DB7)
  +---------------+---------------+---------------+---------------+
  |0 0 0 0 0 1 0 0|1 1 0 0 0 0 0 1|0 0 0 1 1 1 0 1|1 0 1 1 0 1 1 1|
  +---------------+---------------+---------------+---------------+

反転後

        データ             CRC
      -+---------------+  +---------------+---------------+---------------+---------------+
  ...  |1 0 1 1 1 0 1 0|->|1 0 1 1 0 1 1 0|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|
      -+---------------+  +---------------+---------------+---------------+---------------+

                           マジックナンバー (0xEDB88320)
                          +---------------+---------------+---------------+---------------+
                          |1 1 1 0 1 1 0 1|1 0 1 1 1 0 0 0|1 0 0 0 0 0 1 1|0 0 1 0 0 0 0 0|
                          +---------------+---------------+---------------+---------------+

この変更を加えても、変わらず正しいAE426082という値を得ることができました。

crc32test2.c
#include <stdio.h>
#include <inttypes.h>

/* このバイトを処理した後のCRC32の値を計算する */
uint32_t crcnext(uint32_t crc, unsigned char d, uint32_t magic) {
  int i;
  for (i = 0; i < 8; i++) {                        /* LSBから順に処理する */
    int b = (crc & 1);                             /* 上(反転したので下)から1があふれるかをチェックする */
    crc >>= 1;                                     /* シフトする */
    if ((d >> i) & 1) crc |= UINT32_C(0x80000000); /* データのビットを入れる */
    if (b) crc ^= magic;                           /* 1があふれたらマジックナンバーをXORする */
  }
  return crc;
}

int main(void) {
  const char *d = "IEND";
  uint32_t crc = 0; /* 0で初期化する */
  uint32_t magic = UINT32_C(0xEDB88320); /* 反転したマジックナンバー */
  int i, j;
  for (i = 0; d[i]; i++) {
    crc = crcnext(crc, d[i] ^ (i < 4 ? 0xFF : 0), magic); /* 最初の4バイトはビット反転する */
  }
  /* データの最後に4バイトの0x00を入れる */
  for (j = 0; j < 4; j++) {
    crc = crcnext(crc, i + j < 4 ? 0xFF : 0, magic);
  }
  printf("%08"PRIX32"\n", ~crc);
  return 0;
}

データのビット反転と0x00の追加を消す

reverse()の処理を消すことが出来ましたが、正直に言って後処理を消してもあまり嬉しくないです。
やはり計算中の処理を単純にしたいですね。
そこで、今度は「データの最初の4バイトを反転する」という仕様を消します。

まず、「データの最初の4バイトを反転する」という処理を、
「データに『最初の4バイトが0xFF、残りのバイトが全て0x00』というバイト列をXORしたものを投入する」と解釈しなおします。

さらに、バイト列の最初の4バイト、すなわち4バイトの0xFFの部分を最初からCRCの値に投入しておきます。
このとき、CRCの値の初期値は0なので、この投入ではマジックナンバーとのXORは発生しません。

これに対応するため、データのビットの投入の仕方を「CRCの値の最下位(反転後の最上位)に入れる」から
「CRCの値の最上位(反転後の最下位)にXORする」にします。
XORの計算には分配法則や交換法則が成り立つので、このようにしても問題ありません。
この変更では、「データを1ビット投入する→シフトする→1があふれたらマジックナンバーをXORする」という流れは変わりません。

さらに、このようにしておくと、データを最後まで投入するとデータの後ろに4バイトの0x00があるかのような状態になります。
なぜなら、データの後ろにバイト列があったとしても、その値は参照されず、XORされないので、0をXORするのと同じになります。
したがって、データの反転操作を消すついでに、「データの後ろに4バイトの0x00を追加する」という処理も消すことが出来ました。

順番を反転して計算を開始する状態

        データ                             CRC
      -+---------------+---------------+  +---------------+---------------+---------------+---------------+
  ...  |1 0 1 1 1 0 1 0|1 0 1 1 0 1 1 0|->|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|
      -+---------------+---------------+  +---------------+---------------+---------------+---------------+

データとビット反転を表すバイト列を分ける

        ビット反転を表すバイト列
      -+---------------+---------------+
  ...  |1 1 1 1 1 1 1 1|1 1 1 1 1 1 1 1|
      -+---------------+---------------+   CRC
                                      |   +---------------+---------------+---------------+---------------+
                                     (+)->|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|
                                      |   +---------------+---------------+---------------+---------------+
      -+---------------+---------------+
  ...  |0 1 0 0 0 1 0 1|0 1 0 0 1 0 0 1|
      -+---------------+---------------+
        データ

データの最初の4バイトをCRCの値に投入した状態

        ビット反転を表すバイト列
      -+---------------+---------------+
  ...  |0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|
      -+---------------+---------------+   CRC
                                      |   +---------------+---------------+---------------+---------------+
                                     (+)->|1 0 1 1 1 0 1 1|1 0 1 1 0 0 0 1|1 0 1 1 1 0 1 0|1 0 1 1 0 1 1 0|
                                      |   +---------------+---------------+---------------+---------------+
      -+---------------+---------------+
  ...  |0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|
      -+---------------+---------------+
        データ

データの位置をずらし、反転を表すバイト列の0xFFの部分をCRCの初期値にする

        (ビット反転を表すバイト列)         CRC
      -+---------------+---------------+  +---------------+---------------+---------------+---------------+
  ...  |0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|->|1 1 1 1 1 1 1 1|1 1 1 1 1 1 1 1|1 1 1 1 1 1 1 1|1 1 1 1 1 1 1 1|
      -+---------------+---------------+  +---------------+---------------+---------------+---------------+
                                                                                                         ^
                                                                                                        (+)
                                                                                                         |
         -+---------------+---------------+---------------+---------------+---------------+---------------+
     ...  |0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|0 1 0 0 0 1 0 0|0 1 0 0 1 1 1 0|0 1 0 0 0 1 0 1|0 1 0 0 1 0 0 1|
         -+---------------+---------------+---------------+---------------+---------------+---------------+
           データ

データを最後まで投入すると、ちょうどデータの後ろに4バイトの0x00が追加された状態になる

        (ビット反転を表すバイト列)         CRC
      -+---------------+---------------+  +---------------+---------------+---------------+---------------+
  ...  |0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|->|0 1 0 1 0 0 0 1|1 0 1 1 1 1 0 1|1 0 0 1 1 1 1 1|0 1 1 1 1 1 0 1|
      -+---------------+---------------+  +---------------+---------------+---------------+---------------+
                                                                                                         ^
                                                                                                        (+)
                                                                                                         |
                         -+---------------+---------------+---------------+---------------+---------------+
                     ...  |0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|0 0 0 0 0 0 0 0|
                         -+---------------+---------------+---------------+---------------+---------------+
                           データの後ろに仮想的に存在する0x00の列

この変更を加えても、変わらず正しいAE426082という値を得ることができました。

crc32test3.c
#include <stdio.h>
#include <inttypes.h>

/* このバイトを処理した後のCRC32の値を計算する */
uint32_t crcnext(uint32_t crc, unsigned char d, uint32_t magic) {
  int i;
  for (i = 0; i < 8; i++) {     /* LSBから順に処理する */
    int b;
    if ((d >> i) & 1) crc ^= 1; /* データのビットを最上位(反転したので最下位)にXORで入れる */
    b = (crc & 1);              /* 上(反転したので下)から1があふれるかをチェックする */
    crc >>= 1;                  /* シフトする */
    if (b) crc ^= magic;        /* 1があふれたらマジックナンバーをXORする */
  }
  return crc;
}

int main(void) {
  const char *d = "IEND";
  uint32_t crc = UINT32_C(0xFFFFFFFF);   /* 0xFFFFFFFFで初期化する */
  uint32_t magic = UINT32_C(0xEDB88320); /* 反転したマジックナンバー */
  int i;
  for (i = 0; d[i]; i++) {
    crc = crcnext(crc, d[i], magic); /* 1バイト投入して更新する */
  }
  printf("%08"PRIX32"\n", ~crc);
  return 0;
}

テーブルを導入する

今の実装でも一応CRC32を求めることはできますが、データ1バイトの処理に多くのステップを使い、計算コストが大きくなってしまいます。
そこで、テーブルを利用することで計算コストを下げましょう。

まず、改良した処理の構造をもう一度よく観察してみます。

 CRC
+---------------+---------------+---------------+---------------+
|1 1 1 1 1 1 1 1|1 1 1 1 1 1 1 1|1 1 1 1 1 1 1 1|1 1 1 1 1 1 1 1|
+---------------+---------------+---------------+---------------+
                                                               ^
                                                              (+)
                                                               |
                                               -+---------------+
                                           ...  |0 1 0 0 1 0 0 1|
                                               -+---------------+
                                                 データ

すると、(反転した)CRCの下位8ビットはデータとXORされますが、
残りの上位24ビットは今扱っているデータの影響を直接受けず、下位8ビットとデータのXORによって決まる値がXORされることがわかります。
また、XOR演算には交換法則や結合法則が成り立つので、データのビットとマジックナンバーのXORの順番が入れ替わっても問題ありません。
したがって、(反転した)CRCの上位24ビットを固定すると、このデータのバイトを処理した後のCRCの値は、
今の(反転した)CRCの下位8ビットとこのデータのバイトのXORによって決まることがわかります。

そこで、上位24ビットを0に固定し、下位8ビットの値256通りそれぞれについて処理した後のCRCの値を計算し、テーブルに入れておきます。
データの処理では、(反転した)CRCの値の下位8ビットとデータのバイトをXORし、その添字でテーブルを引き、
さらに(反転した)CRCの値の上位24ビットとXORをとることで次のCRCの値が計算できます。
このとき、上位24ビットとのXORは、データの処理でCRCが8ビットシフトされているはずなので、
それに合わせてシフトしてからXORをとります。

この変更を加えても、変わらず正しいAE426082という値を得ることができました。

crc32test4.c
#include <stdio.h>
#include <inttypes.h>

int main(void) {
  const char *d = "IEND";
  uint32_t crc = UINT32_C(0xFFFFFFFF);   /* 0xFFFFFFFFで初期化する */
  uint32_t magic = UINT32_C(0xEDB88320); /* 反転したマジックナンバー */
  uint32_t table[256];                   /* 下位8ビットに対応する値を入れるテーブル */
  int i, j;

  /* テーブルを作成する */
  for (i = 0; i < 256; i++) {      /* 下位8ビットそれぞれについて計算する */
    uint32_t table_value = i;      /* 下位8ビットを添え字に、上位24ビットを0に初期化する */
    for (j = 0; j < 8; j++) {
      int b = (table_value & 1);   /* 上(反転したので下)から1があふれるかをチェックする */
      table_value >>= 1;           /* シフトする */
      if (b) table_value ^= magic; /* 1があふれたらマジックナンバーをXORする */
    }
    table[i] = table_value;        /* 計算した値をテーブルに格納する */
  }

  /* テーブルを用いてCRC32を計算する */
  for (i = 0; d[i]; i++) {
    crc = table[(crc ^ d[i]) & 0xff] ^ (crc >> 8); /* 1バイト投入して更新する */
  }
  printf("%08"PRIX32"\n", ~crc);
  return 0;
}

まとめ

CRCの基本的な計算方法、誤りをより検出しやすくするためのCRC32における工夫、
そして処理を減らして計算コストを下げる工夫をすることで、
多くのサイトで紹介されているようなテーブルを用いたCRC32の計算方法を導出することができました。

37
31
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
37
31

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?