どんなことをするか
利用者は、最初に1~64の整数の中から1個選びます。
システムは数字のリストを提示し、その中に利用者が選んだ数字があるか、という質問をしていきます。
利用者は、その質問に「はい」か「いいえ」で正直に答えていきます。
6回質問に答えると、システムは利用者が選んだ数字を言い当てます。
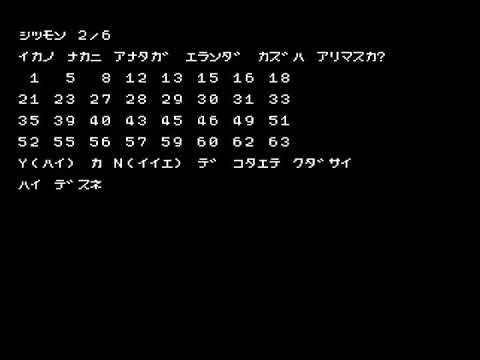
実行結果(YouTube)
この例では、「15」を選んでいます。
ソースコード
10 'エランダ カズ ヲ アテル
20 CLS:?"ジュンビ チュウ...":I=0
30 [I]=I:I=I+1:IFI<64:GOTO30
40 I=63
50 D=RND(I+1):T=[D]:[D]=[I]
60 [I]=T:I=I-1:IFIGOTO50ELSECLS
70 ?"アナタガ エランダ カズヲ アテマス":?
80 ?"1カラ 64マデノ セイスウノ ナカカラ"
90 ?"ドレカ 1コ エランデ クダサイ":?
100 ?"エランダラ ナニカ キーヲ オシテ クダサイ"
110 IF INKEY()=0 GOTO110
120 A=0:Q=0
130 CLS:?"シツモン ";Q+1;"/6":?
140 I=64
150 [I]=0:I=I+1:IF I<72 GOTO150
160 I=0
170 D=[I]/8+64:M=1<<([I]%8)
180 IF I&(1<<Q) [D]=[D]|M
190 I=I+1:IF I<64 GOTO170
200 ?"イカノ ナカニ アナタガ エランダ カズハ アリマスカ?":?
210 P=0:I=0
220 IF ([I/8+64]&(1<<(I%8)))=0:GOTO250
230 N=I+1:IF N<10:?" ";
240 ?N;:P=P+1:IF P%8=0 ?:? ELSE ?" ";
250 I=I+1:IF I<64 GOTO220
260 ?"Y(ハイ) カ N(イイエ) デ コタエテ クダサイ":?
270 K=INKEY()&223:IFK=0 GOTO270
280 IF K=89 ?"ハイ デスネ":A=A|(1<<Q):GOTO310
290 IF K=78 ?"イイエ デスネ":GOTO310
300 GOTO270
310 WAIT 60:Q=Q+1:IF Q<6 GOTO130
320 CLS:?"アナタガ エランダ カズ ハ ";
330 WAIT 60:?".";:WAIT 60:?".";
340 WAIT 60:?".":?:WAIT 60
350 ?[A]+1:?:?"デスネ!":?
解説
簡単のため、0~7の整数の中から選ばれた数を当てることを考えます。
これらの整数は、(先頭の0を含め)3桁の二進数で表すことができます。
二進数 十進数
000 0
001 1
010 2
011 3
100 4
101 5
110 6
111 7
これらの二進数の各桁を見て、1になっている数(十進数)を集めます。
1になっている桁 1になっている数
下から1番目 1 3 5 7
下から2番目 2 3 6 7
下から3番目 4 5 6 7
これらの「1になっている数」のリストをそれぞれ提示し、選んだ数があるかどうかを質問していきます。
すると、「ある(はい)」という答えなら二進数のその桁が1、
「ない(いいえ)」という答えなら二進数のその桁が0であることがわかります。
その結果、3回の質問で二進数が完全にわかり、対応をみることで選ばれた数もわかります。
同様に、$0$から$2^n-1$までの整数は(先頭の0を含め)$n$桁の二進数で表すことができるので、
どの数を選んだかは$n$回の質問でわかります。
このまま質問をしても選ばれた数を当てることはできますが、
質問が露骨に二進数そのままになってしまうため、つまらないと思いました。
そこで、二進数と十進数の関係をシャッフルしておきます。
ついでに、十進数にそれぞれ1を足し、1~8 ($1$から$2^n$) の中から当てるようにしてみました。
二進数 十進数
000 2
001 7
010 6
011 8
100 3
101 5
110 1
111 4
これらの二進数の各桁を見て、1になっている数を集めます。
1になっている桁 1になっている数
下から1番目 7 8 5 4
下から2番目 6 8 1 4
下から3番目 3 5 1 4
順番がバラバラだと選んだ数があるかがわかりにくいので、集めた数をそれぞれ昇順にソートします。
1になっている桁 1になっている数
下から1番目 4 5 7 8
下から2番目 1 4 6 8
下から3番目 1 3 4 5
パッと見では法則がわかりにくくなったように思えます。
さて、問題はどうやってソートするかです。
今回は数十個の要素をソートすることを考えます。
バブルソートは実装が単純ですが、要素数の2乗にだいたい比例する時間がかかってしまいます。
それでも現代の普通のパソコンであれば一瞬でできますが、IchigoJamでは時間がかかりすぎてしまいます。
マシン語を使う?いいえ、今回はソート対象のより詳しい性質を用いた、もっと簡単な方法を用います。
今回のソート対象は、あらかじめ値の範囲が決まった整数であり、しかもその範囲の幅は十分小さいです。
さらに、同じ整数が1回のソートの対象に複数回現れることはありません。
そこで、以下の方法で昇順への並べ替えを行います。
- 考えられる値それぞれに対応するフラグを用意し、全てfalseで初期化します。
- ソート対象のデータを見て、出てきた値に対応するフラグをtrueにしていきます。
- 全部のデータについて処理をしたら、フラグを対応する値が小さい方から順にチェックしていきます。
- フラグがfalseなら何もせず、trueなら対応する値を結果に追加します。
すると、「要素数+値の範囲の大きさ」にだいたい比例する時間で昇順に並べ替えた結果が得られます。
これなら、IchigoJamでも違和感の少ない時間で並べ替えの結果を得ることができました。
IchigoJamとは
2,000円前後で購入することができ、BASICによるプログラミングが可能なパソコンです。
こどもパソコン IchigoJam - はじめてのプログラミングパソコン(1500円)
また、プログラムをWebブラウザ上で実行できるサービスもあります。
※「IchigoJam」はjig.jpの登録商標です