PNGのデコーダ実装を目指す (2) zlib (deflate) 圧縮データ

ここに PNG の仕様書がある。
Portable Network Graphics (PNG) Specification (Third Edition)
これは、この PNG の仕様書をもとに PNG ファイルから画像データを取り出すプログラムを作るための学習をするシリーズである。

PNGにおける圧縮データ

10. Compression

現在、PNG における圧縮は圧縮形式 0 のみが定義されている。
これは、圧縮されたデータとして deflate 圧縮されたデータが格納された zlib ストリームを使用するものである。

画像データ (スキャンライン) を圧縮した zlib ストリームは、IDAT チャンクに格納されたデータを順に1個ずつすべて結合することで得られる。

また、以下のチャンクにも、同様に圧縮したデータが含まれる。(これらのチャンクでは、1個の zlib ストリームを複数のチャンクに分割することはない)

• 11.3.2.3 iCCP Embedded ICC profile
• 11.3.3.4 iTXt International textual data (圧縮を行うかは選択できる)
• 11.3.3.3 zTXt Compressed textual data

zlib ストリーム

RFC 1950 - ZLIB Compressed Data Format Specification version 3.3

全体の構造

zlib ストリームは、以下のデータからなる。

バイト数	内容
1	CMF (Compression Method and flags)
1	FLG (FLaGs)
0 or 4	DICTID (プリセット辞書識別子)
可変	圧縮データ
4	ADLER32 (Adler-32 checksum)

CMF・FLG

合計2バイトで、圧縮形式の情報を表す。
以下の構造になっている。
それぞれのフィールド内では、上位のビットをバイトのMSB側に、下位のビットをバイトのLSB側に格納する。

バイト  0 (CMF)          1 (FLG)
ビット  7 6 5 4 3 2 1 0  7   6    5   4 3 2 1 0
       +-+-+-+-+-+-+-+-+---+---+-----+-+-+-+-+-+
       | CINFO |   CM  | FLEVEL|FDICT|  FCHECK |
       +-+-+-+-+-+-+-+-+---+---+-----+-+-+-+-+-+
        MSB         LSB MSB                 LSB

CINFO (Compression info) : 4ビット

CM の値が 8 のとき、LZ77 の窓サイズを表す。
このとき、CINFO の値 $n$ は窓サイズが $2^{n+8}$ であることを表す。
すなわち、CINFO の値と窓サイズの関係は以下のようになる。

CINFO	窓サイズ
0	256
1	512
2	1,024
3	2,048
4	4,096
5	8,192
6	16,384
7	32,768

現在、CINFO の値として 8 以上を用いることはできない。
また、CM の値が 8 以外のときは、CINFO は未定義である。

CM (Compression method) : 4ビット

使用されている圧縮アルゴリズムを表す。
以下の値が定義されている。

CM	圧縮アルゴリズム
8	32K までの窓サイズを用いた deflate アルゴリズム

これ以外の値は、現在定義されていない。

FLEVEL (Compression level) : 2ビット

CM の値が 8 (deflate) の場合は、以下を表す。
これは、再圧縮を行う価値がありそうかの判定に用いることができるが、展開には不要な情報である。

FLEVEL	圧縮レベル
0	最も速いアルゴリズムを用いて圧縮した
1	速いアルゴリズムを用いて圧縮した
2	デフォルトのアルゴリズムを用いて圧縮した
3	最も遅く、圧縮効果が最高のアルゴリズムを用いて圧縮した

FDICT (Preset dictionary) : 1ビット

FLG の後に DICTID を配置するかを表す。

FDICT	意味
0	DICTID を配置しない (すぐに圧縮データを配置する)
1	4 バイトの DICTID を配置する

FCHECK (check bits for CMF and FLG) : 5ビット

CMF と FLG をビッグエンディアンの 16 ビット符号なし整数としてみたとき、31 の倍数になるような値を設定する。
すなわち、

$$
\left(\textrm{CMF}\times 256 + \textrm{FLG}\right) \bmod 31 = 0
$$

となるような値を設定する。

DICTID

プリセット辞書の識別子を表す。

「プリセット辞書」とは、圧縮結果には反映しない、圧縮器に最初に入力するバイト列である。
DICTID を配置する場合は、このバイト列の Adler-32 チェックサムを DICTID に設定する。

ADLER32

圧縮前/展開後のデータの Adler-32 チェックサムを格納する。
プリセット辞書が存在する場合でも、プリセット辞書のデータはチェックサムの対象には含めない。

Adler-32 チェックサム

Adler-32 チェックサムは、以下のアルゴリズムで求まる 4 バイトのチェックサムである。

def adler32(input_bytes):
    s1 = 1
    s2 = 0
    for b in input_bytes:
        # s1 : 全バイトの値の和 mod 65521
        s1 = (s1 + b) % 65521
        # s2 : 全 s1 の値の和 mod 65521
        s2 = (s2 + s1) % 65521
    return s2 * 65536 + s1

求まった値を、4 バイトのビッグエンディアン (上位のバイトほど先) で格納する。

PNG における制約

PNG の圧縮形式 0 においては、zlib で用いる設定に以下の制約がある。

• 圧縮アルゴリズム (CM) は 8 (deflate) を指定する
• LZ77の窓サイズ (CINFO) は 7 (32,768 バイト) 以下を指定する
• プリセット辞書が存在してはいけない (FDICT は 0 を指定する)

圧縮を行うデータが 16,384 バイト以下の場合は、窓サイズをデータサイズを 2 のべき乗に切り上げた値に設定することで、圧縮率に影響を与えずにエンコードおよびデコードに必要なメモリの量を減らすことができる。

deflate 圧縮データ

RFC 1951 - DEFLATE Compressed Data Format Specification version 1.3

deflate は、バイト列を (通常はより短い) ビット列で表現 (エンコード) する方法である。
エンコード結果のビット列は、バイト列に変換して表現される。

全体の構造

deflate 圧縮データは、1個または複数のブロックを並べたものである。
ブロックの境界はバイトの境界にあるとは限らず、あるバイトの途中にブロックの境界がある可能性もある。
ブロックの中にそれが最後のブロックかを表す情報があり、圧縮データの終端は最後のブロックの終端である。

データのバイト列への格納方法

deflate では、1 バイト未満の大きさのデータをよく扱う。
一方、現代の多くのコンピュータでは、データはバイト単位で扱う。
そこで、1 バイト未満のデータの列をバイト列の中に格納する方法を定義する。

deflate では、以下の規則でデータを配置する。

• 各バイトの下位 (LSB) から上位 (MSB) に向かってデータを配置する。
• それぞれのデータは、下位を先 (バイトの LSB 側) に、上位を後 (バイトの MSB 側) に配置する。
• データがバイトからはみ出す場合は、次のバイトの下位から続けて配置する。

たとえば、データ列

[1101, 0, 10011, 01, 110]

(先頭の0を含む桁数がそれぞれのデータの大きさ (ビット数) を表す)
をこの規則に沿ってあるバイトの最初から格納すると、

[01101101, ?1100110]

となる。(? の部分にはまだデータが格納されていない)
このとき、データ列のそれぞれの要素は以下の位置に配置されている。

[22210000, ?4443322]

すなわち、データ列全体を大きなリトルエンディアンの整数とみて、下位から順に取り出したい長さのビット列を取り出すことで、格納されているデータ列を取り出すことができる。

圧縮データの表現 (リテラル・参照・終端)

各ブロック内のバイト列は、リテラル・参照・終端の 3 種類の要素を用いて表される。
これらの要素は、0 ～ 285 のコードにより表現される。
それぞれのコードは以下の意味を持つ。

コード	意味
0 ～ 255	リテラル
256	終端
257 ～ 285	参照 (繰り返し回数)

これらの圧縮データのコードは、後述のハフマン符号によりエンコード (ビット列に変換して格納) される。

リテラル

コード 0 ～ 255 は、それぞれ値 0 ～ 255 (コードと同じ値) を持つ 1 バイトのデータを出力 (展開結果) に加えることを表す。

参照

コード 257 ～ 285 は、以前に展開の結果出力したバイト、もしくは展開結果の最初のバイトの前にあるプリセット辞書中のバイトを繰り返して出力することを表す。
以下の 4 個のデータを順に配置し、参照する位置とこの操作を繰り返す回数を表す。

長さ	データ
ハフマン符号で決まる	繰り返し回数を表すコード (257 ～ 285)
繰り返し回数を表すコードで決まる	繰り返し回数に足す値
ハフマン符号で決まる	参照する位置を表すコード (0 ～ 31)
参照する位置を表すコードで決まる	参照する位置に足す値

繰り返し回数を表すコード、および参照する位置を表すコードは、それぞれ後述のハフマン符号を用いてエンコード (ビット列として格納) する。
これらのビット列の長さは、符号を読み取りながら決定する。
なお、「繰り返し回数を表すコード」(圧縮データのコード) のエンコードと「参照する位置を表すコード」のエンコードでは、一般に別のハフマン符号のセットが用いられる。

それぞれに足す値は、コードごとに対応する足す値のビット数が決まっており、通常の整数として表現 (ビット列に格納) される。
コードによっては足す値のビット数が 0 のこともあり、この場合の足す値は 0 である。
コードごとに対応する繰り返し回数や位置が決まっており、これらにそれぞれに足す値を足すことで、具体的な繰り返し回数や位置がわかる。

繰り返し回数を表すコードの定義

コード	繰り返し回数	足す値のビット数
257	3	0
258	4	0
259	5	0
260	6	0
261	7	0
262	8	0
263	9	0
264	10	0
265	11	1
266	13	1
267	15	1
268	17	1
269	19	2
270	23	2
271	27	2
272	31	2
273	35	3
274	43	3
275	51	3
276	59	3
277	67	4
278	83	4
279	99	4
280	115	4
281	131	5
282	163	5
283	195	5
284	227	5
285	258	0

参照する位置を表すコードの定義

コード	参照する位置	足す値のビット数
0	1	0
1	2	0
2	3	0
3	4	0
4	5	1
5	7	1
6	9	2
7	13	2
8	17	3
9	25	3
10	33	4
11	49	4
12	65	5
13	97	5
14	129	6
15	193	6
16	257	7
17	385	7
18	513	8
19	769	8
20	1025	9
21	1537	9
22	2049	10
23	3073	10
24	4097	11
25	6145	11
26	8193	12
27	12289	12
28	16385	13
29	24577	13

繰り返し回数は最大で $258$、参照する位置は最大で $24577 + \left(2^{13}-1\right) = 32768$ となる。

参照する位置は、これまでに出力した展開結果のバイト列の前に (存在する場合) プリセット辞書を連結したバイト列の後ろから何番目かで表す。
参照の対象は、現在のブロック内のバイトとは限らず、以前のブロックやプリセット辞書内のバイトもとりうるが、プリセット辞書の先頭 (プリセット辞書が存在しない場合は展開結果のバイト列の先頭) より前は参照できない。
また、今回の繰り返し中に新たに出力したバイトが参照の対象になる可能性もある。

たとえば、ここまでの展開結果のバイト列が

0x11 0x22 0x33 0x44 0x55 0x66 0x77 0x88

で、参照を表すデータが

• 繰り返し回数を表すコード 262
• (繰り返し回数に足す値を表す数値 0ビット)
• 参照する位置を表すコード 4
• 参照する位置に足す値を表す数値 1 (1ビット)

の場合、繰り返し回数は $8$、参照する位置は $5 + 1 = 6$ となり、新たにバイト列

0x33 0x44 0x55 0x66 0x77 0x88 0x33 0x44

が出力 (展開結果) に追加される。

終端

コード 256 は、このブロックの終わりを表す。
このブロックが最終ブロックでない場合、終端を表すビット列 (ハフマン符号) の直後から次のブロックが始まる。

ハフマン符号

ハフマン符号は、語頭符号である。
すなわち、セット内のどの符号も他の符号の接頭辞になっておらず、符号列の先頭を見るだけでそれがどの符号に対応しているかが一意に定まる。

deflate では、以下のコードを、それぞれ別のハフマン符号のセットでエンコード (ビット列に変換) する。

• 圧縮データのコード (リテラル・参照 (繰り返し回数)・長さ) 0 ～ 285
• 参照する位置のコード 0 ～ 29
• 符号のビット数のコード 0 ～ 18

さらに、これらのセットはブロックごとに存在し、別の可変ハフマン符号ブロックでは一般に別のセットを用いる。
(固定ハフマン符号ブロックでは、圧縮データのコードと参照する位置のコードは共通であり、符号のビット数のコードは用いない。また、無圧縮ブロックではハフマン符号を用いない)

deflate で用いるハフマン符号は、以下の性質を持つ。

• 短い符号は、長い符号よりも辞書順で前である
• 同じ長さの符号では、より前のコードに対応する符号が辞書順で前である

この性質を持つ符号を、以下のアルゴリズムにより生成する。
アルゴリズムの入力 bit_length は、コード i を表す符号の長さ (ビット数) を bit_length[i] に格納したリストである。

# 符号の長さごとに、その長さの符号で表すコードを数える
# length_count[i] = ビット数 i の符号で表すコードの数
# ビット数 0 は「そのコードには符号を割り当てない」ことを表し、ビット数 0 で表す符号は無い
length_count = [0 for _ in range(max(bit_length) + 1)]
for n in bit_length:
    # ビット数が 0 ではない (符号を割り当てる) ときのみカウントする
    if n > 0:
        length_count[n] += 1

# 符号の長さごとの、最初のハフマン符号を求める
# next_huffman[i] : ビット数 i の符号で表すコードに次に割り当てるハフマン符号
next_huffman = [0 for _ in length_count]
# i を 1 から (length_count の要素数 - 1) まで繰り返す
for i in range(1, len(length_count)):
    # 前のビット数の最初の符号を表す数値に前のビット数の符号の個数を足し、
    # さらに 1 ビット左シフト (2 倍) する
    next_huffman[i] = (next_huffman[i - 1] + length_count[i - 1]) << 1

# それぞれのコードに対応するハフマン符号を求める
# huffman[i] : コード i に対応するハフマン符号
huffman = [None for _ in bit_length]
for i in range(len(bit_length)):
    # コード i に対応するハフマン符号のビット数を n とする
    n = bit_length[i]
    # ビット数が 0 ではないときのみ符号を割り当てる
    if n > 0:
        # next_huffman[n] の値を n 桁の 2 進数で表し、ハフマン符号とする
        huffman[i] = format(next_huffman[n], "0%db" % n)
        # ビット数 n の符号で表すコードに割り当てるハフマン符号を進める
        next_huffman[n] += 1

たとえば、コード 0 ～ 6 を表す符号のビット数がそれぞれ以下であったとする。

コード	符号のビット数
0	3
1	4
2	2
3	3
4	3
5	2
6	4

すると、ビット数ごとの符号の個数と、最初の符号を表す整数は以下のようになる。

符号のビット数	符号の個数	最初の符号
1	0	0
2	2	0
3	3	4
4	2	14

そして、それぞれのコードに対応する符号は以下のようになる。

コード	符号のビット数	符号 (十進)	符号 (二進)
0	3	4	100
1	4	14	1110
2	2	0	00
3	3	5	101
4	3	6	110
5	2	1	01
6	4	15	1111

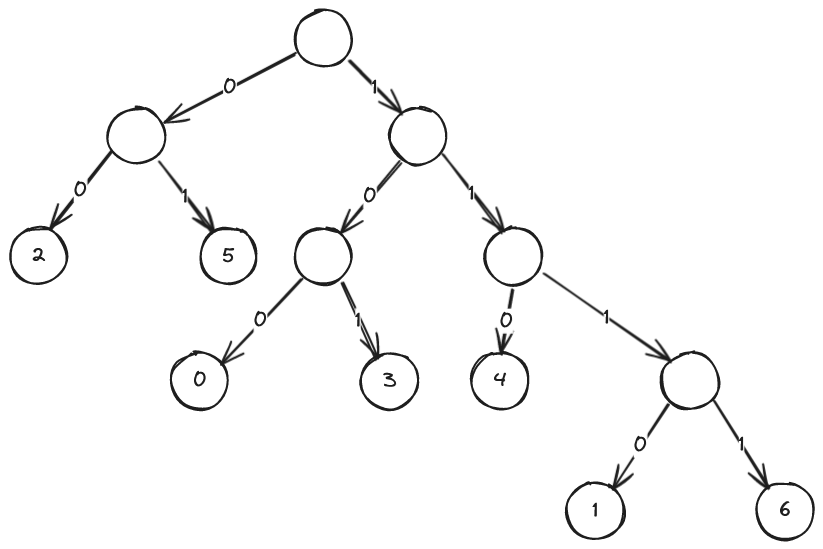
ハフマン符号は、符号中の 0/1 を木のエッジに、復号結果のコードを葉に割り当てたニ分木で表現できる。
この木のルートから符号列中の 0/1 に従って降りていき、葉に到達したらそこに割り当てられたコードを出力してルートに戻ることにより、ハフマン符号の復号ができる。
たとえば、この例の符号は以下のような木で表せる。

$n$ ビットのハフマン符号は、「$n$ ビットのデータ 1 個」ではなく、「1 ビットのデータ $n$ 個」として圧縮データに格納する。
すなわち、通常の整数データとは逆に、符号の前をバイトの LSB 側、後ろをバイトの MSB 側に格納する。
こうすることで、データ列からデータを 1 ビットずつ取り出し、それに沿って木をたどって復号ができるようになる。
(圧縮データの「参照」で用いる「足す値」は通常の整数データであり、下位ビットをバイトの LSB 側、上位ビットをバイトの MSB 側に格納する)

ブロックの構造

各ブロックの先頭には、以下のデータを格納する。

ビット数	名前	役割
1	BFINAL	最終ブロックフラグ
2	BTYPE	ブロックの種類

BFINAL は、このブロックが最終ブロックかを表す。

BFINAL	意味
0	最終ブロックではない (このブロックの終端の後に次のブロックがある)
1	最終ブロックである (このブロックの終端が圧縮データの終端)

BTYPE は、このブロックの種類を表す。

BTYPE	意味
00 (0)	無圧縮ブロック
01 (1)	固定 (fixed) ハフマン符号ブロック
10 (2)	可変 (dynamic) ハフマン符号ブロック
11 (3)	予約 (エラー)

無圧縮ブロック

まず、上記 BTYPE の直後から次のバイトの境界までのデータ (0～7 ビット) を無視 (スキップ) する。
次に、以下のデータ (バイト列) を格納する。

バイト数	データ
2	LEN : 無圧縮データのバイト数
2	NLEN : LEN をビット反転 (ビットNOT) した値
LEN	無圧縮データ

LEN および NLEN はリトルエンディアン (下位バイトを先) で格納する。
展開時は、無圧縮データ (バイト列) をそのまま出力データに加える。

固定 (fixed) ハフマン符号ブロック

BTYPE の直後から、以下の (固定の) 長さのハフマン符号を用いて圧縮データのコード列を表現し、格納する。
このタイプのブロックで用いるハフマン符号の長さは固定であるため、データとしては格納しない。
(具体的な符号は、deflate で用いる符号の定義と符号のビット数から求まる)

コード	符号のビット数
0 ～ 143	8
144 ～ 255	9
256 ～ 279	7
280 ～ 287	8

参照する位置のコード (0 ～ 31) は、全てビット数 5 のハフマン符号で表す。

なお、圧縮データのコード 286・287 および参照する位置のコード 30・31 は符号の定義には含まれるが、実際は用いられないはずである。

可変 (dynamic) ハフマン符号ブロック

BTYPE の直後から、以下の仕様に沿ってこのブロックで用いるハフマン符号の長さの情報を格納する。
その後、このハフマン符号で表現された圧縮データのコード列を格納する。

ハフマン符号の長さの情報は、以下の形式で格納される。

ビット数	情報
5	HLIT: 圧縮データのコード用符号の長さ情報の数 - 257
4	HDIST: 参照する位置のコード用符号の長さ情報の数 - 1
4	HCLEN: 符号のビット数のコード用符号の長さ情報の数 - 4
3 × (HCLEN + 4)	符号のビット数のコード用符号の長さ情報
ハフマン符号で決まる	圧縮データ・参照する位置のコード用符号の長さ情報

符号のビット数のコードは 0 ～ 18 であり、それぞれ以下の意味を持つ。
「ある符号のビット数が 0」というのは、「その符号 (に対応するコード) はこのブロックでは用いられない」ことを表す。

コード	意味
0 ～ 15	次の 1 個の符号のビット数は 0 ～ 15 (コードと同じ) である
16	次の $n_{16}$ 個の符号のビット数は、直前の符号のビット数と同じである
17	次の $n_{17}$ 個の符号のビット数は 0 である
18	次の $n_{18}$ 個の符号のビット数は 0 である

コード 16 ～ 18 で用いる整数 $n_{16}, n_{17}, n_{18}$ は、それぞれのコードを表すハフマン符号の直後にそれぞれ決まった長さの整数データを置き、それにより決定する。

コード	整数データのビット数	整数の求め方
16	2	$n_{16} = \textrm{整数データ} + 3$
17	3	$n_{17} = \textrm{整数データ} + 3$
18	7	$n_{18} = \textrm{整数データ} + 11$

符号のビット数のコード用符号の長さ情報は、それぞれの符号のビット数を 3 ビットの整数データで表し、以下の順番で格納する。
HCLEN が 15 未満 (長さ情報の数が 19 未満) のとき、存在しない後ろの方の符号のビット数は 0 である。

位置と符号のビット数のコードの対応

位置	符号のビット数のコード
0	16
1	17
2	18
3	0
4	8
5	7
6	9
7	6
8	10
9	5
10	11
11	4
12	12
13	3
14	13
15	2
16	14
17	1
18	15

圧縮データ・参照する位置のコード用符号の長さ情報は、まとめて符号のビット数のコードを表すハフマン符号 (および $n_{16}, n_{17}, n_{18}$ を表す整数データ) で格納する。
まず圧縮データのコード 0 ～ (HLIT + 256) それぞれに対応する符号のビット数を順に格納し、続けて参照する位置のコード 0 ～ HDIST それぞれに対応する符号のビット数を順に格納する。
すなわち、符号のビット数のコードを表すハフマン符号により、合計で (HLIT + HDIST + 258) 個の符号のビット数が表現される。

PNGのデコーダ実装を目指すシリーズ

• (1) ファイルとチャンクの構造
• (2) zlib (deflate) 圧縮データ