More than 1 year has passed since last update.

整数に整数を掛けて整数を伝える方法を考えた

Last updated at 2022-01-05Posted at 2022-01-05

問題

Twitterで以下の問題を発見しました。

AさんとBさんとCさんがゲームをします
最初に、 C さんはある正整数 X, Y をAさんに渡します
A さんは X に好きな整数を掛けて B さんに渡します
このとき、 B さんが Y を知る方法を考えてください
なお、 A さんと B さんは事前に話し合って方法を共有することができます
— まぐふらい (@magrofly) January 5, 2022

そこで、この問題の条件で、AさんがBさんにYを伝える方法を考えてみました。

他の皆さんの方法

効率が悪い方法

皆さんの答案を見ると、素因数分解をしたり、Y乗したり、
Y桁の数やY番目の〇〇を用いたりといった方法が多くみられました。

素因数分解は今のところ難しい処理であり、十進数で300桁程度の数でも分解できないことがあります。
また、Y乗やY桁の数やY番目の〇〇は、十進数で30桁程度のYでも現代の計算機では扱いきれないほど大きく、または遠くなるでしょう。

間違った方法

簡単のため Y は平方数でないとして、以下の手順を考えます。
・A さんは XY を掛け、B さんは受け取った数をできるだけ大きい平方数で割った残りを答える。

チェス盤の問題で、盤にマス目が無限にありマスに正の整数の番号があるとします。
— SSRS (@SSRS_cp) January 5, 2022

Yが平方数のときにどうするかが書かれていない上、Yが平方数でなくてもうまくいかない場合があります。

平方数（へいほうすう、square number）とは、一般的には整数の自乗（二乗）で表される非負整数のことである。ただし広義の意味では有理数の二乗であれば平方数という。

平方数 - Wikipedia

例えば $X = 1, Y = 18$ とすると、$Y = {(\pm 3 \sqrt{2})}^2$であり、$\sqrt{2}$が有理数でないことは有名な証明があります。
よって、$Y$は平方数ではありません。

$X \times XY = 18$ であり、平方数 $9 = 3^2$ で割った商は$2$、余りは$0$です。
よって、「残り」の定義がよくわかりませんが、
「できるだけ大きい平方数で割った残り」は$Y = 18$にはならないと考えられます。

未解析

整数の符号化、log(N)+O(log*(N)) とかで出来そう？
だからO(Ylog*(Y)) 倍まで思いついた
Z=00001(Yを表す適当な符号)(あまりの桁)
となるようにXの倍数を作れて、このZのサイズがlog(X)+log(Y)+log*(Y)
— hotman (@hotmanww) January 5, 2022

できるのかよくわかりませんが、実現すれば自分の方法より効率がよくなるかもしれません。

自分の方法

$Y$を3進数で表します。この時の桁数を$k$、下から$i$番目の桁を$Y_i$とします。
$i$番目に小さい素数を$p_i$とし、$f(n, i)$を${p_i}^m$が$n$を割り切る最大の整数$m$とします。
以下の条件を満たす整数$\alpha$を求めます。
- $i = 1, \ldots , k$ について、$f(\alpha X, i) \mod 4 = Y_i$
- $f(\alpha X, k + 1) \mod 4 = 3$
$\alpha X$ をBさんに渡します。

小さい素数をそれそれ高々3回掛けるので、掛けた結果が無駄に大きくなりすぎるのを避けられます。
さらに、$Y$を表す情報の次に$3$を置くことで終端を表し、無駄に大きい素因数を求めなくていいようにしています。

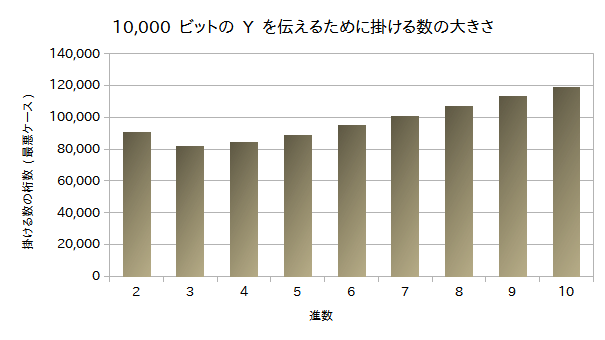
2進数や4進数などでもいいですが、実験の結果3進数が一番最悪ケースで掛けた結果が小さくなりやすいようでした。
例えば、$Y$が10,000ビットの時、掛ける数$\alpha$の十進数での桁数は以下のようになりました。

実装

Aさん、Bさんともに、$i$番目に小さい素数をエラトステネスの篩の応用で求めています。
$i$番目に小さい素数がいくつになるかわからないので、素数を求める範囲を少しずつ伸ばしていきます。
$n$までの素数が求まっている時$n^2$までの範囲の素数を求めることができ、
今回の実装で一回に求める範囲はこれより少ないので、この方法で求まります。

Aさん

コマンドライン引数で$X$と$Y$の値をこの順に指定できます。
コマンドライン引数を1個だけ渡した場合、その値を$X$とみなし、標準入力から$Y$の値を読み込みます。
コマンドライン引数なしで起動した場合、標準入力の最初の行を$X$、次の行を$Y$とします。

Bさんに渡す数を標準出力に出力します。

encoder.py

import sys

list_length = 4
primes = [2, 3]

def nth_prime(n):
	global list_length
	global primes
	while len(primes) <= n:
		delta_length = list_length // 32 + 1
		is_prime = [True] * delta_length
		old_list_length = list_length
		list_length += delta_length
		for p in primes:
			for i in range((old_list_length + p - 1) // p * p, list_length, p):
				is_prime[i - old_list_length] = False
		primes += [i + old_list_length for i, v in enumerate(is_prime) if v]
	return primes[n]

X = int(sys.argv[1]) if len(sys.argv) > 1 else int(sys.stdin.readline().rstrip())
Y = int(sys.argv[2]) if len(sys.argv) > 2 else int(sys.stdin.readline().rstrip())

radix = 3

x_work = X
y_work = Y
alpha = 1
pos = 0
while y_work > 0:
	p = nth_prime(pos)
	d = y_work % radix
	y_work //= radix
	count = 0
	while x_work % p == 0:
		x_work //= p
		count += 1
	while count % (radix + 1) != d:
		alpha *= p
		count += 1
	pos += 1

p = nth_prime(pos)
count = 0
while x_work % p == 0:
	x_work //= p
	count += w
while count % (radix + 1) != radix:
	alpha *= p
	count += 1

print(alpha * X)

Bさん

コマンドライン引数でAさんから渡される数を指定できます。
コマンドライン引数なしで起動した場合、標準入力からAさんから渡される数を読み込みます。

$Y$の値を標準出力に出力します。

decoder.py

import sys

list_length = 4
primes = [2, 3]

def nth_prime(n):
	global list_length
	global primes
	while len(primes) <= n:
		delta_length = list_length // 32 + 1
		is_prime = [True] * delta_length
		old_list_length = list_length
		list_length += delta_length
		for p in primes:
			for i in range((old_list_length + p - 1) // p * p, list_length, p):
				is_prime[i - old_list_length] = False
		primes += [i + old_list_length for i, v in enumerate(is_prime) if v]
	return primes[n]

value = int(sys.argv[1]) if len(sys.argv) > 1 else int(sys.stdin.readline().rstrip())

radix = 3

value_work = value
Y = 0
pos = 0
delta = 1
while True:
	assert value_work > 1
	p = nth_prime(pos)
	count = 0
	while value_work % p == 0:
		value_work //= p
		count += 1
	d = count % (radix + 1)
	if d == radix:
		break
	Y += delta * d
	delta *= radix
	pos += 1

print(Y)

実行例

まずは小さい数で実験してみました。

$ python encoder.py 1 1
54
$ python decoder.py 54
1
$ python encoder.py 1 18
8575
$ python decoder.py 8575
18
$ python encoder.py 12345 67890
93182011756845
$ python decoder.py 93182011756845
67890

この例では、$X$と$Y$が101桁ずつ、Aさんが渡した数が609桁でした。

$ cat test1_X_Y.txt
27182818284590452353602874713526624977572470936999595749669676277240766303535475945713821785251664274
31415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
$ python encoder.py < test1_X_Y.txt > test1_value.txt
$ cat test1_value.txt
440524372659803146819405941984938020171867562997633539105452801908325982511905932416237199363093844045036847911337275280849134204883445362366308666169921867206004498013971130272411877568469353933662614910785642274891535550542596342208629343244263200114752814059931320786908550424183213557541334348913304519555296839087093492037012393660398695265917021342302473371592188582105722834580253762273205165926166600113001335573274192066612633605321322713858307023641285748403740413001243670119499940327428312578291957034928523148055989931633234495008508072254150723656916209311489517014184639077570106895866732231760
$ python decoder.py < test1_value.txt
31415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679

この例では、$X$が1000桁、$Y$が992桁、Aさんが渡した数(長いので省略)が9004桁でした。

$ cat test2_X_Y.txt
6954668118360507330752739341396920203092235510508041194623235642881513961309339238315637160227428695255059064498559797998284837214806798758170197796883984505409610677398157798119242257605063809621260717518675278209192836063197287833717652571550036112693346073873056835479033986998436724982235084279683167009045717706910365116223472439587020870077034198158863121033600778405682296536485521843711552262032556364218605688365664492771770259938165305349083930110833914296144607104190863205957078206496247972609726492116411384911809992457035407807663328296779146692409437681126031404232426891128059631826125769737571727341029165952586884713286643108124336315507866034092911609664654345395196960956274627382763225197667272262064724055693985777277655085904116623014695958812117182609027208753331426917859314280300004442747829793269955092822288531729902402818866765811586749631955697370875033618306472309289517700071853591362648589153021236344845664493768201272166520127137294675819588849704950042971193046875
30089562055206958251751697282330589121651734796611526762974214826487299622782704747820054653285966087690886733929494698327476528939721047810102858323904413144762597012683028221356497198842614635172436015993789691800106149705935189173626083830395582231541313534013114003913403027431605381446963314101244353688421348857780556152699403527425878886940610759108036814764886496341327451022862464119504218638151153029518879173224495380013544892976832743789742946392003064149585790293219452173314484204619295155804692741678537697539732671008294424993085654821379463448271911840100407297289417151478167468810530161338940269449151194958946289480777924744129787573455156971698191516921189059885119404218620508501852055284523146131732179243487634506727861385942871978507911418728889814089795961727739255465311903909028057301077450080162369933919979541254649994994988413441230707713853626091414736462695582172954843711217401795255757269882282708462763719961329042617329659337668423704471604264300596724234
$ time python encoder.py < test2_X_Y.txt > test2_value.txt

real    0m0.127s
user    0m0.015s
sys     0m0.015s
$ time python decoder.py < test2_value.txt
30089562055206958251751697282330589121651734796611526762974214826487299622782704747820054653285966087690886733929494698327476528939721047810102858323904413144762597012683028221356497198842614635172436015993789691800106149705935189173626083830395582231541313534013114003913403027431605381446963314101244353688421348857780556152699403527425878886940610759108036814764886496341327451022862464119504218638151153029518879173224495380013544892976832743789742946392003064149585790293219452173314484204619295155804692741678537697539732671008294424993085654821379463448271911840100407297289417151478167468810530161338940269449151194958946289480777924744129787573455156971698191516921189059885119404218620508501852055284523146131732179243487634506727861385942871978507911418728889814089795961727739255465311903909028057301077450080162369933919979541254649994994988413441230707713853626091414736462695582172954843711217401795255757269882282708462763719961329042617329659337668423704471604264300596724234

real    0m0.181s
user    0m0.015s
sys     0m0.000s

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up